
HA+H,O-A-+H K,=[AH,0+] THAT 酸性强度可用pK表示,pK,定义为-1gK,即pK。=一lgK,K>1,则pK<O,为强酸;K< 10~4则pK,>4为弱酸。 碱的强度可以类似地由碱的离解常数K。来测定: B+H,0一BH+OH 太-9 碱的强度可用pK表示,pK,定义为一gK,即pKb=一lgK。也可将上述平衡写成该碱的共 酸BH的离解平衡: BH+H,0一B+H,O K.-[B tant) pk,=-IgK. 若已知K,K,可由水的离解带数及K。求得,因为上述K,与K,的乘积为水的离解常数K: K.·Kb=Km=1.0×10-1“故pK.+pK。=14 下列反应式平衡很大程度向右偏移: HCI+CH,COO-CH,COOH+CI- 因为HC1是强酸,CH,COO是弱酸CH,COOH的共轭碱,强酸将质子转移形成弱酸。如用氯负 离子处理乙酸,基本上不发生反应。这样,通过平衡位置的测量,可以确定酸和碱的相对强度,如 表1-3,1-4所列出的是常见的无机酸及有机酸的pK,其中有机酸是按酸的强度递降次序排列 的。碳原子上的氢,酸性很弱,称氢碳酸,如CH,PK,≈49,是最弱的酸。 表1-3无机酸的酸性25C) 分子式 P. 分子式 PE。 -5.2 (HO)PO 2.15(pK:2,7.2pK3,12.38 -47 (H0):SO: -5.2pK,21.00) HF (HO)SO 1.8(pK.2,7.2) H:C Br 15.74 HOCI HONO -1.3 NH HONO 3.23 C0,H0 6,35(pK2,10.40 28
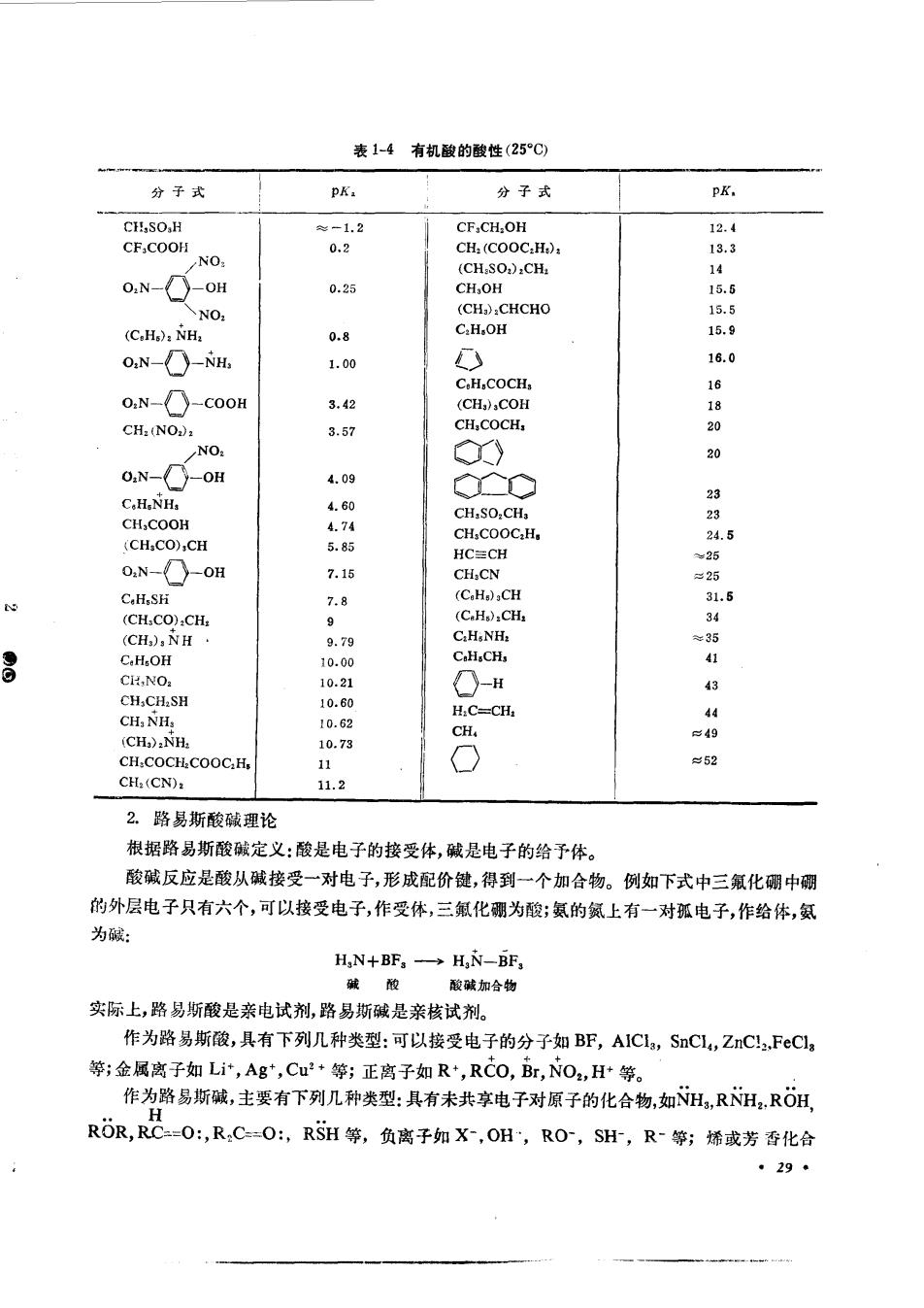
表1-4有机酸的酸性(25C 分子式 pK. 分子式 pK. CH.SO.H CF.CH.OH CF:COOH 0.2 CH:(CO C.HO (CH.SO).CH. 1 ON-OH 0.25 CH,OH 15.5 (CH:CHCHO (C.H.):NHa C.H.OH 8 ON-NH 1.00 16.0 O.N-D-COOH 16180 CH:(NO, 3.57 NO ◆) O.N-OH 4.09 C.H.NH. CH,COOH CH.SO.CH, (CHCO),CH 5.8时 CH,COOC:H 245 HC≡CH .N-0H 7.15 CH.CN ¥25 7.8 ts C.H,SH 9 C.HaNB: C.H.CH. 4 H 43 CH.CH.SH 10.60 H.C-CH. CH:NHs 10.62 s49 (CH):NH. CH 10.73 ≈52 CH:(CN) 11.2 2。路易斯酸碱理论 根据路易斯酸碱定义:酸是电子的接受体,碱是电子的给予体。 酸碱反应是酸从碱接受一对电子,形成配价健,得到一个加合物。例如下式中三氟化硼中硼 的外层电子只有六个,可以接受电子,作受体,三氟化硼为酸;氨的氨上有一对孤电子,作给体,氨 为藏: H,N+BF,→H,-F 碱酸 酸碱加合物 实际上,路易斯酸是亲电试剂,路易斯碱是亲核试剂。 作为路易斯酸,具有下列几种类型:可以接受电子的分子如BF,AIC1,SnCL,ZnC,FcCl, 等;金属离子如Li,Ag,Cu+等;正离子如R+,RC0,Br,NO2,H等。 作为路易斯碱,主要有下列几种类型:具有未共享电子对原子的化合物,如NH,RNH,ROH RR,RC=O:,R,C=O:,RSH等,负离子如X,OH,R0,SH,R-等;烯或芳香化合 4290

物等。 路易斯酸与勃朗斯德酸两著没省多大区别而路易斯酸知比勃期斯德酸带围广泛,并把质子 也作为酸。按勃朗斯德定义,把产生质子的分子或离子(如HCL,NH,)称为酸,而按路易斯定义却 把它们作为酸碱加合物。 1.13有机反应中的热力学与动力学 热力学与动力学将提供数据,以获得有关反应能否进行以及反应速率、反应机制等的信息。 所谓反应机制,是对一个反应如何进行的很详细的描述,这种描述是根据很多实验事实总结后提 出来的,它有一定的适用范围,能解释很多事实,并能预测反应的发生,如果发现新的实验事实 不能解释,就要提出新的反应机制,反应机制已成为有机结构理论的一部分。 1.热力学与化学平衡 热力学是研究一个反应能否进行、进行的程度,即反应物有多少转化成生成物,是一个化学 平衡问题,它与反应物及生成物的性质、外界反应条件如温度、压力有关,它与反应速率没有 关系。 一个可逆反应在一定祖度下达到平衡时,它的平衡常数K就是生成物浓度乘积与反应物浓 度乘积之比,例如: A+B-C+D K-RTB 根据热力学,平衡常数与势能(除动能以外的全部能量)变化关系为: △Ge=-RT1nK △G°是势能的变化,是在标准状态下生成物与反应物势能之差,R为摩尔气体常数(8.314× 10-3kJmo11.K-1),T为反应时的热力学温度[T=(t+273)K]。 从上面关系式看出,当△G°<0时,平衡常数K>1,平衡对生成物有利;当△G>0时,K< 1,平衡对反应物有利,因此根据△G的大小,可以预测反应能否进行。计算出一个反应的△G, 使平衡位置的计算也有可能。而△G°又与下列两个热力学数据有关: △G°=△H◆-T△8 △H“是焓变,是在标准状态下生成物与反应物焓之差,基本上是反应物与生成物之间的健能差, 即所有形成新键的健能之和减去所有断裂的健的键能之和。如为放热反应,△H°为负值;吸热 反应,△H°为正值。如果反应附体积不变,△H通常接近于△E(生成物与反应物能量之差),即 △H=△E+AV(当△V=0,△H=△B)。△S°是痛变,是在标准状态下生成物与反应物熵之差。 熵可以看作是体系内的混乱度,因此熵变也就是在反应过程中体系内熵的变化,混乱度增加,△S~ 为正值,对反应有利;混乱度减少,△8°为负值,对反应不利。在A+B→C+D反应中,反应物 与生成物的分子数相等,熵变是比较小的;在A一→B+C反应中,生成物的分子数增加,因此室 间可能有更多的排列,熵变往往是大的,很多反应中,熵变可以忽略不计,但在有些反应中,熵变 。30

很重要,而且可以支配烙。 △G°是△Ⅲ°与T△S°两项综合的结果,而平衡常数又与△G°有关,因此平衡常数可表 示为: △He-TASe=-RTInK 可暨111计算下列反应的焓变: CH,CH-CHCH+H一→CH,CH,CH,CH,(健能数据查表2-1O) 可题1-12化合物A转为化合物B时的焓变为一7kJ·mol(25C,如△S可忽酪不计,请计算平衡常数K, 并指出A与B的百分含量。 2.动力学与反应速率 使用热力学方法推测反应时,有一个局限性,它只能说明反应能否进行及进行的程度。而动 力学能够提供这个反应的反应速率及反应所需的条件。如果不存在比较合适的反应条件,即使在 热力学上倾向于发生反应的两个分子,可以反应很慢或无限期地存在下去而不发生反应,因此还 必须深人了解反应过程中各步的反应速率及反应所需条件是非常重要的。如氯甲烷在OH水 溶液中于25℃反应: CH,C1-+OH-CH,OH+CI- K-886-1o △Ge=-RT1nK∴.△Ge=-92kJmo1 △C°是一个大的负值,因此从热力学数据表明,这个反应是可以进行的,但用开始浓度为 0.05molL-1CH,C1在开始浓度为0.1molL-NaOH水溶液中,在室温放置两天,只有10%发生 了反应,即反应速率很慢,如在50℃反应,反应速率快50倍。这是因为分子间接近,才能发生反 应,但当分子间接近到一定程度,就有排斥力,因此存在一个能垒,必需提供能量,克服这个能垒, 迫使分子接近才能发生反应,克服这个能垒所必需的最低的能量,称话化能(activation energy), 用B。表示。上述反应尽管是放热反应,但仍然必希提供104,6kJ·mo1活化能,因此提高反应 温度,才能使上述反应顺利进行。这些是动力学研究的问题。 反应速率是在单位时间内反应物的浓度或生成物的浓度的变化,如: →B+ 速率=-A]=-B=-drC=,[A] 因为反应物A的浓度随时间诚少,故出现负号。方括弧表示反应物或生成物的浓度。上述反应 速率与反应物A的浓度成正比,该反应为一级反应,k为一级反应的速率常数,单位为$。 又如: A+B→C+D 速率=-&=L[ATB町 反应速事与两种反应物的浓度成正比,反应物A和B的反应级数均为一级,其和为二级,故该反 。31

应是二级反应,为二级反应速率常数,单位为mol1Ls1。又如: 2A+BC+D 速率=[A]B] 方括弧上指数是实验测定的,该反应方括孤上全部指数的和为三级,因此是三级反应。按物质的 悬计算,A的消失必须是B的两倍。 习题1-13CH,C1+0H →CH,OH+C该反应在某温度的反应速率常数k一6×10·mo-1L·5,请根 据巳给的浓度计算反应速率。 (i)0.1 mol.L-ICH,Cl1.0 mol-L-OH- (ii)0.01 mol-L-CH,Cl1.0 mol-L-OH- (iii)0.01 mol-L-CH,Cl 0.01 mol-L-OH- 化学动力学主要是观察反应物或生成物的浓度随时间变化而改变,用各种方法跟踪反应物 的消失或生成物的出现,就可以测定某一反应的反应速率,例如用波谱分析可以快速而有效地连 续监测浓度的改变,测定旋光可以跟踪溶液中旋光物质的反应情况,连续H测定可以监测质子 的生成或消耗,等等,只要有测定反应物或生成物浓度的方法,就可以用来测定反应速率,从而得 到反应的级数,再计算反应速率常数k值。对于某一特定反应,仅是反应温度的函数,与反应 物浓度无关。 那末动力学的理论根据是什么呢? (1)碰撞理论:根据阿仑尼乌斯(Arrhenius),速率公式: 速率=PZe-,1RT ?为碰撞频率,它与反应物浓度有关,浓度愈大,碰撞机会愈多;P为取向几率,并不是所有碰 撞均有效,只有在一定取向时才有效;e~/r为能是几率(为自然对数的底,EB,为活化能,R 为摩尔气体常数,T为热力学温度),分子必需吸收足够的能量,才能使分子活化,因此能量几率 是指具有最低活化能的碰撞分数,能量几率与温度关系很大,温度每升高10℃,反应速率将提高 一倍左右。 碰撞理论中存在很多不足,如P值计算很困难,活化能又与什么因素相联系禁等,因此后来 发展了过渡态理论。 (2)过渡态理论:过渡态理论强调分子相互作用的状态,并将活化能与过渡态联系起来。当 反应物相互接近的反应进程中,出现一个能显比反应物与生成物均高的势能最高点,与此势能最 高点相应的结构称为过渡态(transition s1ate),用“≠"表示,过渡态极不稳定,只是反应进程中 的一个中间阶段的结构,不能分离得到 A+BC-[A.B.C]→AB+C 反位物过诚态 生成物 如反应物A接近BC,要与BC成健而未完全形成,BC之间的健开始伸长而未断裂,这种反应物 到过渡态之间的键的变化,迫使势能上开,当势能到达活化能这个数值时,反应物到达过渡态,这 时A与B之间进一步结合成键,B与C之间的键进一步削弱、断镜,势能下降,释放能最,得到生 成物。△H°为反应前后体系能量的变化。如图1-26所示, ·32