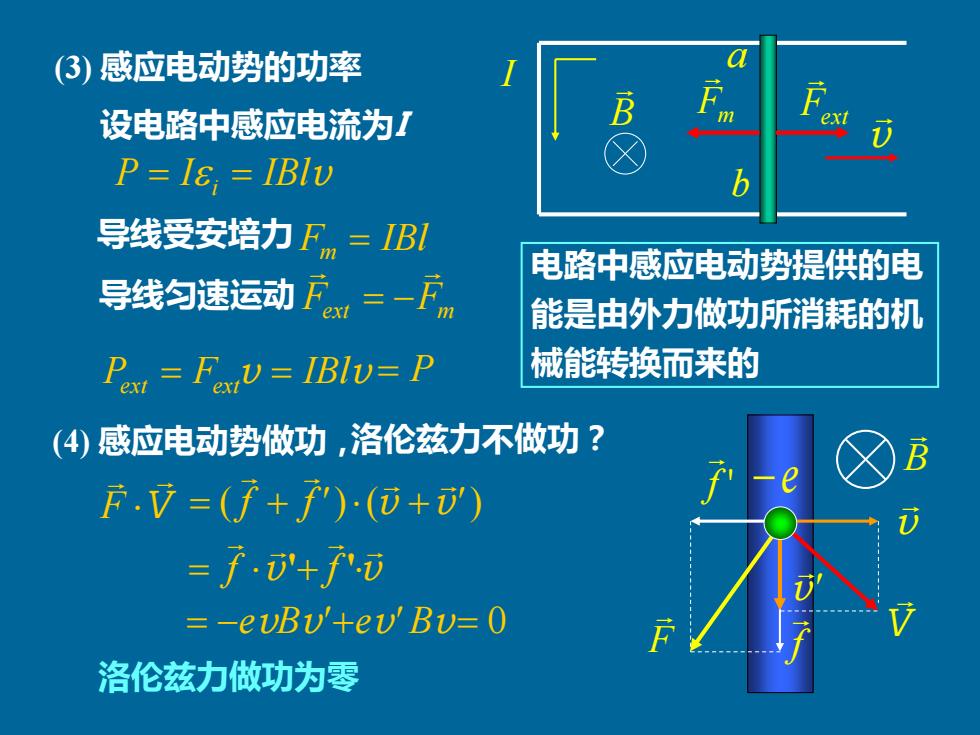
(3)感应电动势的功率 设电路中感应电流为I P=I8 IBlv 导线受安培力Fm=IBl 电路中感应电动势提供的电 导线匀速运动广=一F 能是由外力做功所消耗的机 Pox FoxU IBlv=P 械能转换而来的 (4)感应电动势做功,洛伦兹力不做功? F.7=(f+)(⑦+) =f.+f0 =-evBU'+evBU=0 洛伦兹力做功为零
(3) 感应电动势的功率 设电路中感应电流为I B v a b 导线受安培力 导线匀速运动 电路中感应电动势提供的电 能是由外力做功所消耗的机 械能转换而来的 (4) 感应电动势做功,洛伦兹力不做功? B v f V f ' F V F ( f f ') (v v') = + + v v = f '+ f ' = −evBv'+ev' Bv= 0 −e v' P = I i = IBlv F IBl m = Fext Fm = − Pext = Fextv = IBlv = P Fm Fext I 洛伦兹力做功为零
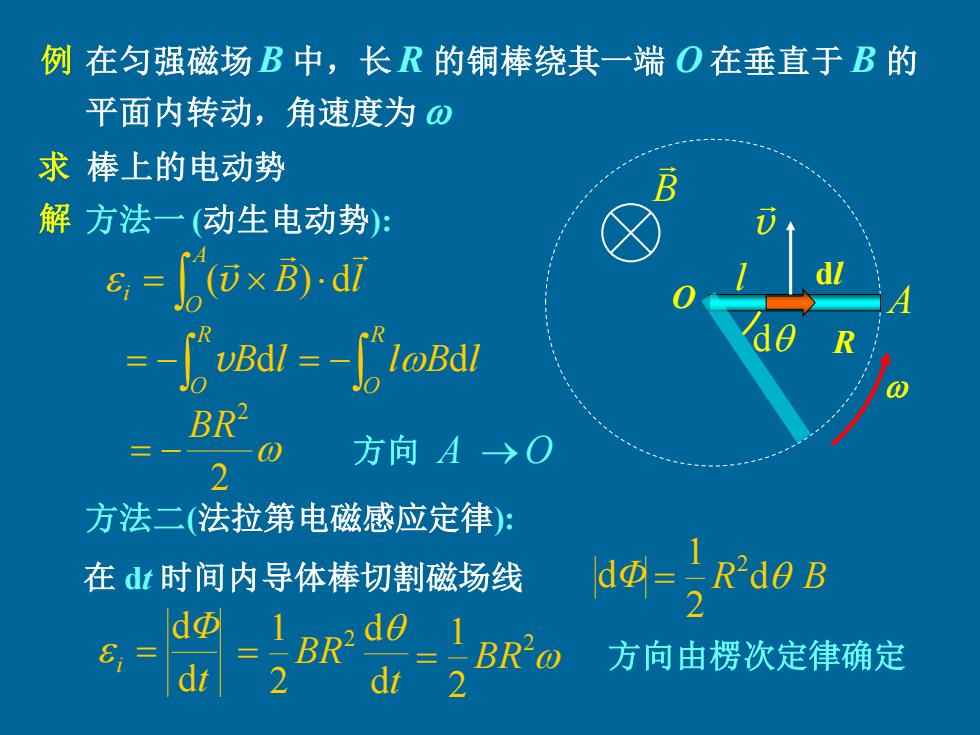
例在匀强磁场B中,长R的铜棒绕其一端O在垂直于B的 平面内转动,角速度为⊙ 求棒上的电动势 解方法一(动生电动势) 8,= gox刷d @Bdl BR2 方向A→C 2 方法二(法拉第电磁感应定律): 在dt时间内导体棒切割磁场线 dΦ= -R2de B dΦ 1 =BR2@ 方向由楞次定律确定 2 dt
例 在匀强磁场B 中,长 R 的铜棒绕其一端 O 在垂直于 B 的 平面内转动,角速度为 B O R 求 棒上的电动势 解 方法一 (动生电动势): dl A l = A O i B l (v ) d = − R O vBdl = − R O lBdl 2 2 BR = − 方向 A →O 方法二(法拉第电磁感应定律): 在 dt 时间内导体棒切割磁场线 dΦ v d R d B 2 1 2 = t Φ i d d = t BR d d 2 1 2 = 2 2 1 = BR 方向由楞次定律确定
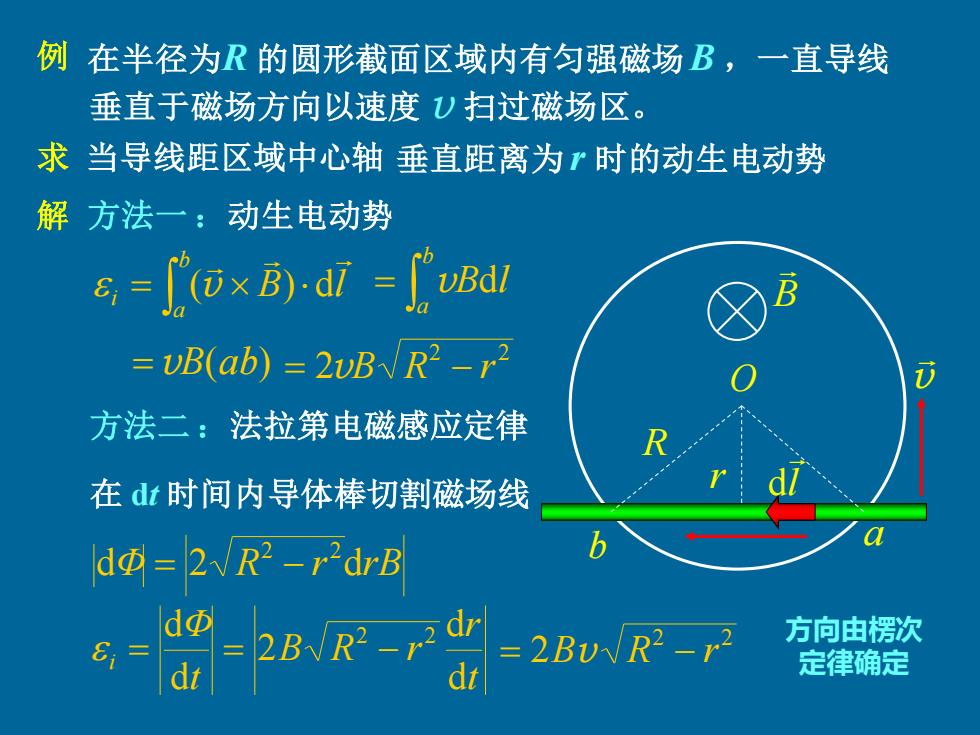
例在半径为R的圆形截面区域内有匀强磁场B,一直导线 垂直于磁场方向以速度)扫过磁场区。 求当导线距区域中心轴垂直距离为r时的动生电动势 解方法一:动生电动势 e,=Dxa=心bd =UB(ab)=2UBR2-r 方法二:法拉第电磁感应定律 在dt时间内导体棒切割磁场线 d④=2WR2-r2drB dΦ =2BR2-rdr =2BUVR2-r2 方向由楞次 dt 定律确定
例 在半径为R 的圆形截面区域内有匀强磁场B ,一直导线 垂直于磁场方向以速度 v 扫过磁场区。 求 当导线距区域中心轴 垂直距离为 r 时的动生电动势 v B r R a b 解 方法一 :动生电动势 = b a i B l (v ) d l d = b a vBdl =vB(ab) 2 2 = 2vB R − r O 方法二 :法拉第电磁感应定律 在 dt 时间内导体棒切割磁场线 dΦ 2 R r drB 2 2 = − t r B R r t Φ i d d 2 d d 2 2 = = − 2 2 = 2Bv R − r 方向由楞次 定律确定

二.感生电动势 ●实验证明:当磁场变化时,静止导体中也出现感应电动势 仍是洛伦兹力充当非静电力?麦克斯韦提出: 无论有无导体或导体回路,变化的磁场都将在其周围空间产 生具有闭合电场线的电场,并称此为感生电场或有旋电场 电场力充当非静电力 感生电动势=心瓦,dl E是感生电场 Φ 闭合回路中 o-fEd-
二. 感生电动势 实验证明:当磁场变化时,静止导体中也出现感应电动势 仍是洛伦兹力充当非静电力? 电场力充当非静电力 麦克斯韦 提出: 无论有无导体或导体回路,变化的磁场都将在其周围空间产 生具有闭合电场线的电场,并称此为感生电场或有旋电场 感生电动势 EV = b a i V E l d 闭合回路中 是感生电场 t Φ E l L i V d d = d = − = − S B S t d d d •

·感生电场与变化磁场之间的关系 aB 讨论 ()感生电场是无源有旋场 静电荷 场源 感生电 变化的磁场(磁生电) 场与静 静电场为保守场 电场的 环流 感生电场为非保守场 比较 静电场为有源场 通量 感生电场为无源场闭合电场线)
= − S S t B d 感生电场与变化磁场之间的关系 讨论 感生电 场与静 电场的 比较 场源 环流 L V E l d 静电荷 变化的磁场 通量 静电场为保守场 感生电场为非保守场 静电场为有源场 感生电场为无源场(闭合电场线) (1) 感生电场是无源有旋场 (磁生电) •