
五、排队论研究的基本问题 1.排队系统的统计推断:即通过对排队系统主 要参数的统计推断和对排队系统的结构分析,判 断一个给定的排队系统符合于哪种模型,以便根 据排队理论进行研究。 2.系统性态问题:即研究各种排队系统的概率 规律性,主要研究队长分布、等待时间分布和忙 期分布等统计指标,包括了瞬态和稳态两种情形。 3.最优化问题:即包括最优设计(静态优化), 最优运营(动态优化) o
11 五、 排队论研究的基本问题 1.排队系统的统计推断:即通过对排队系统主 要参数的统计推断和对排队系统的结构分析,判 断一个给定的排队系统符合于哪种模型,以便根 据排队理论进行研究。 2.系统性态问题:即研究各种排队系统的概率 规律性,主要研究队长分布、等待时间分布和忙 期分布等统计指标,包括了瞬态和稳态两种情形。 3.最优化问题:即包括最优设计(静态优化), 最优运营(动态优化)

六、排队问题求解(主要指性态问题) 求解一般排队系统问题的目的主要是通过研究 排队系统运行的效率指标,估计服务质量,确定系 统的合理结构和系统参数的合理值,以便实现对现 有系统合理改进和对新建系统的最优设计等。 排队问题的一般步骤: 1.确定或拟合排队系统顾客到达的时间间隔 分布和服务时间分布(可实测)。 2.研究系统状态的概率。系统状态是指系统 中顾客数。状态概率用P(t)表示,即在t时刻系统中 有n个顾客的概率,也称瞬态概率
12 六、 排队问题求解(主要指性态问题) 求解一般排队系统问题的目的主要是通过研究 排队系统运行的效率指标,估计服务质量,确定系 统的合理结构和系统参数的合理值,以便实现对现 有系统合理改进和对新建系统的最优设计等。 排队问题的一般步骤: 1. 确定或拟合排队系统顾客到达的时间间隔 分布和服务时间分布(可实测)。 2. 研究系统状态的概率。系统状态是指系统 中顾客数。状态概率用Pn(t)表示,即在t时刻系统中 有n个顾客的概率,也称瞬态概率
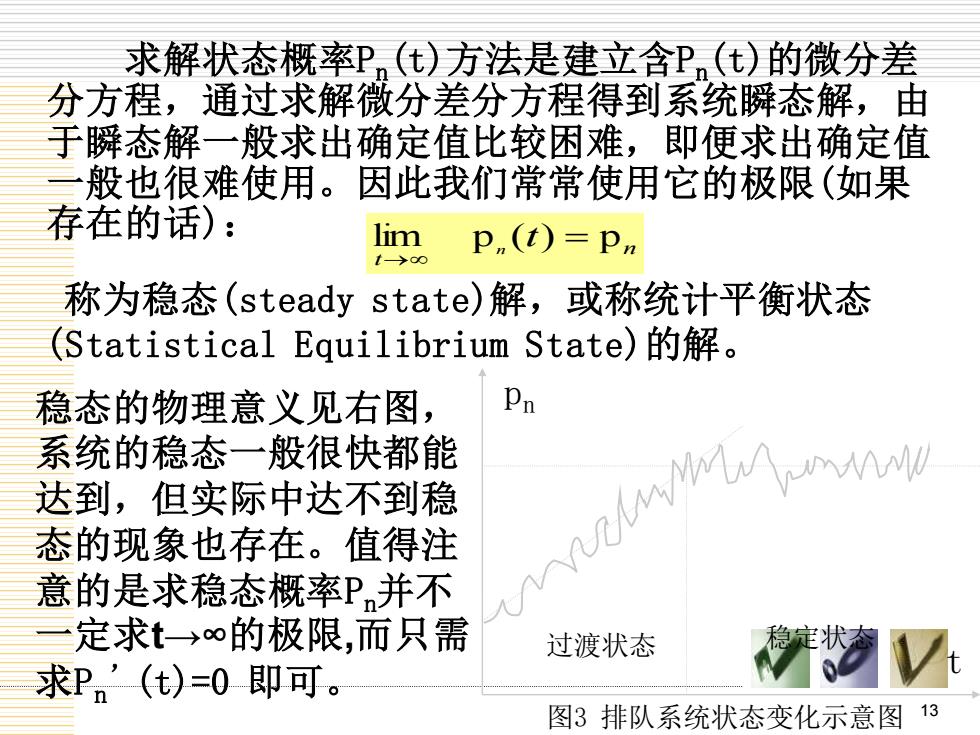
求解状态概率P(t)方法是建立含P(t)的微分差 分方程,通过求解微分差分方程得到系统瞬态解,由 于瞬态解一般求出确定值比较困难,即便求出确定值 般也很难使用。因此我们常常使用它的极限(如果 存在的话): lim p(t)=p t→ 称为稳态(steady state)解,或称统计平衡状态 (Statistical Equilibrium State)的解。 稳态的物理意义见右图, Pn 系统的稳态一般很快都能 达到,但实际中达不到稳 态的现象也存在。值得注 AVZ/wAnANMM 意的是求稳态概率P并不 定求t→∞的极限,而只需 过渡状态 稳定状态 求P。’(t)=0即可。 图3排队系统状态变化示意图3
13 求解状态概率Pn(t)方法是建立含Pn(t)的微分差 分方程,通过求解微分差分方程得到系统瞬态解,由 于瞬态解一般求出确定值比较困难,即便求出确定值 一般也很难使用。因此我们常常使用它的极限(如果 存在的话): n t t lim pn ( ) = p → 稳态的物理意义见右图, 系统的稳态一般很快都能 达到,但实际中达不到稳 态的现象也存在。值得注 意的是求稳态概率Pn并不 一定求t→∞的极限,而只需 求Pn ’(t)=0 即可。 过渡状态 稳定状态 pn t 图3 排队系统状态变化示意图 称为稳态(steady state)解,或称统计平衡状态 (Statistical Equilibrium State)的解
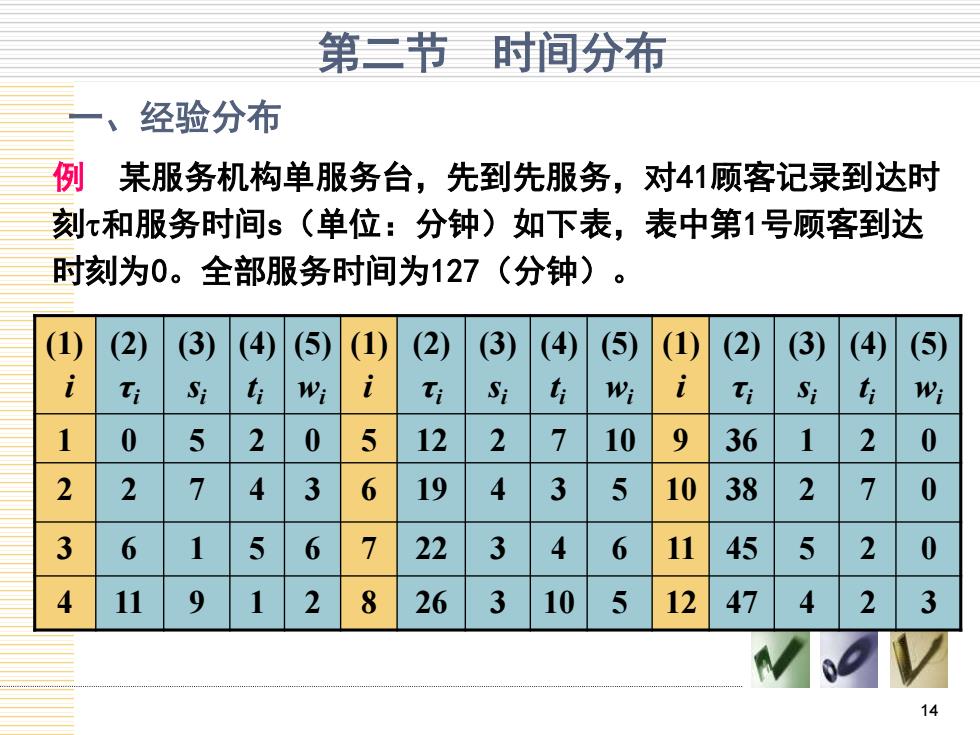
第二节 时间分布 经验分布 例 某服务机构单服务台,先到先服务,对41顾客记录到达时 刻τ和服务时间s(单位:分钟)如下表,表中第1号顾客到达 时刻为0。全部服务时间为127(分钟) 3) 】 (3) 3) (4) 5) Si Wi Ti Si ti W Si ti Wi 0 5 2 0 5 12 2 10 9 36 2 0 2 2 4 3 6 19 4 5 10 38 2 0 3 6 6 7 22 3 4 6 11 45 5 2 0 11 9 1 2 8 26 3 10 5 12 47 4 2 3 14
14 一、经验分布 例 某服务机构单服务台,先到先服务,对41顾客记录到达时 刻和服务时间s(单位:分钟)如下表,表中第1号顾客到达 时刻为0。全部服务时间为127(分钟)。 (1) i (2) τi (3) si (4) t i (5) wi (1) i (2) τi (3) si (4) t i (5) wi (1) i (2) τi (3) si (4) t i (5) wi 1 0 5 2 0 5 12 2 7 10 9 36 1 2 0 2 2 7 4 3 6 19 4 3 5 10 38 2 7 0 3 6 1 5 6 7 22 3 4 6 11 45 5 2 0 4 11 9 1 2 8 26 3 10 5 12 47 4 2 3 第二节 时间分布
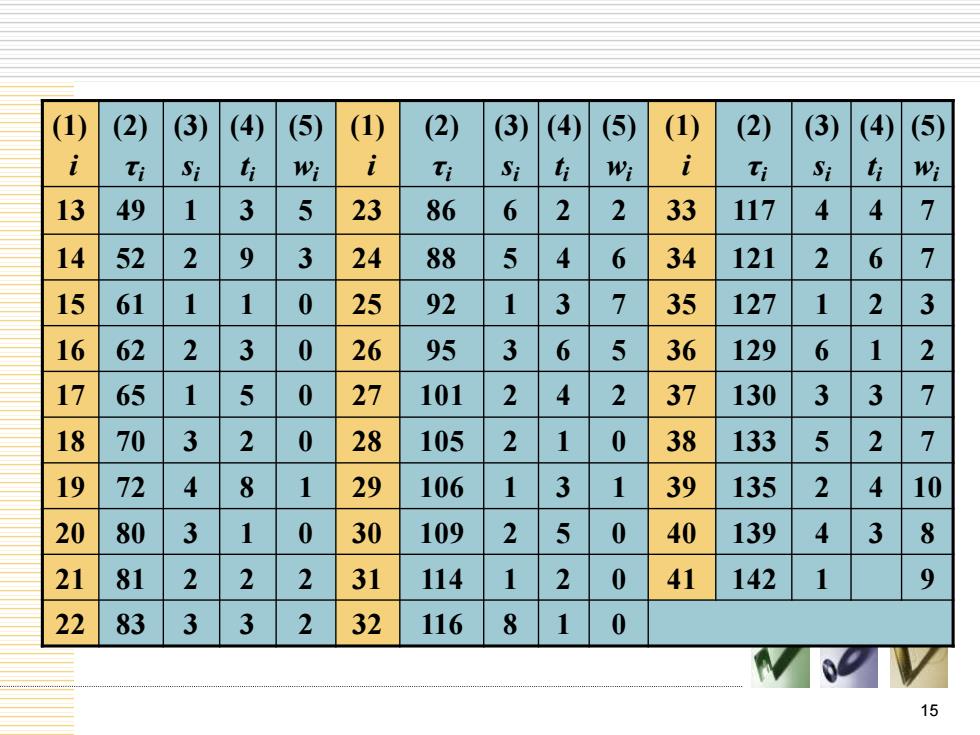
(1) (2) (3) (4) (5) () (2) (3) (4) (5) (1) (2) (3) (4) (⑤) i ti Si ti Wi i ti Si ti Wi i ti Si ti Wi 13 49 1 3 5 23 86 6 2 2 33 117 4 4 7 14 52 2 9 3 24 88 5 4 6 34 121 2 6 7 15 61 1 1 0 25 92 1 3 7 35 127 1 2 3 16 62 2 3 0 26 95 3 6 5 36 129 6 1 2 17 65 5 0 27 101 2 4 2 37 130 3 3 7 18 70 3 2 0 28 105 2 0 38 133 5 2 7 19 72 4 8 1 29 106 1 3 1 39 135 2 4 10 20 80 3 1 0 30 109 2 5 0 40 139 4 3 8 21 81 2 2 2 31 114 2 0 41 142 9 22 83 3 3 2 32 116 8 1 0 15
15 (1) i (2) τi (3) si (4) ti (5) wi (1) i (2) τi (3) si (4) ti (5) wi (1) i (2) τi (3) si (4) ti (5) wi 13 49 1 3 5 23 86 6 2 2 33 117 4 4 7 14 52 2 9 3 24 88 5 4 6 34 121 2 6 7 15 61 1 1 0 25 92 1 3 7 35 127 1 2 3 16 62 2 3 0 26 95 3 6 5 36 129 6 1 2 17 65 1 5 0 27 101 2 4 2 37 130 3 3 7 18 70 3 2 0 28 105 2 1 0 38 133 5 2 7 19 72 4 8 1 29 106 1 3 1 39 135 2 4 10 20 80 3 1 0 30 109 2 5 0 40 139 4 3 8 21 81 2 2 2 31 114 1 2 0 41 142 1 9 22 83 3 3 2 32 116 8 1 0