
第八章动态规划 本章主要内容: 多阶段的决策问题 ◆最优化原理与动态规划的数学模型 离散确定性动态规划模型的求解 离散随机性动态规划模型的求解 一般数学规划模型的动态规划解法 2014-12-15
2014-12-15 1 第八章 动态规划 多阶段的决策问题 最优化原理与动态规划的数学模型 离散确定性动态规划模型的求解 离散随机性动态规划模型的求解 一般数学规划模型的动态规划解法 本章主要内容:

§1多阶段的决策问题 (Multi-Stage decision process) 动态规划: 一是一种研究多阶段决策问题的理论和方法。 多阶段决策问题: 一是指一类活动过程,它可以分为若干个相互联系的阶 段,在每个阶段需要作出决策。这个决策不仅决定 这一阶段的效益,而且决定下一阶段的初始状态。 策略: 一每个阶段的决策确定以后,就得到一个决策序列,称 为策略。多阶段决策问题就是求一个策略,使各阶段 的总效益达到最优。 2014-12-15 2
2014-12-15 2 §1 多阶段的决策问题 (Multi-Stage decision process) 动态规划: –是一种研究多阶段决策问题的理论和方法。 多阶段决策问题 : –是指一类活动过程,它可以分为若干个相互联系的阶 段,在每个阶段都需要作出决策。这个决策不仅决定 这一阶段的效益,而且决定下一阶段的初始状态。 策略: –每个阶段的决策确定以后,就得到一个决策序列,称 为策略。多阶段决策问题就是求一个策略,使各阶段 的总效益达到最优
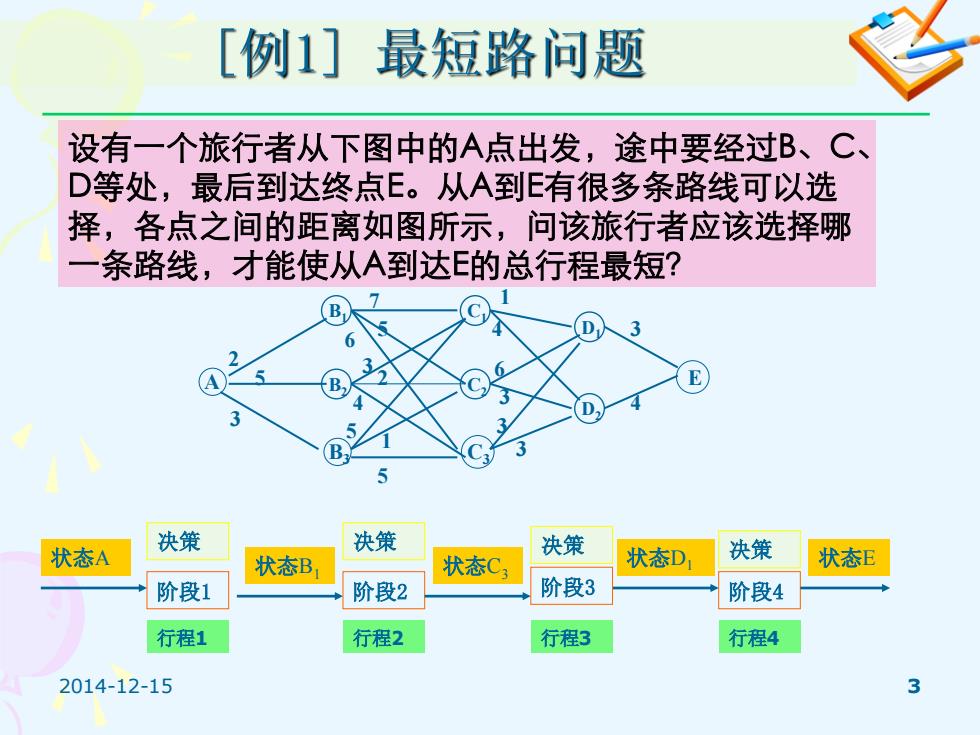
[例1]最短路问题 设有一个旅行者从下图中的A点出发,途中要经过B、C、 D等处,最后到达终点E。从A到E有很多条路线可以选 择,各点之间的距离如图所示,问该旅行者应该选择哪 一条路线,才能使从A到达E的总行程最短? 决策 决策 状态A 决策 状态B, 状态C3 状态D 决策 状态E 阶段1 阶段2 阶段3 阶段4 行程1 行程2 行程3 行程4 2014-12-15 3
2014-12-15 3 [例1] 最短路问题 设有一个旅行者从下图中的A点出发,途中要经过B、C、 D等处,最后到达终点E。从A到E有很多条路线可以选 择,各点之间的距离如图所示,问该旅行者应该选择哪 一条路线,才能使从A到达E的总行程最短? A B1 B2 B3 C3 C2 C1 D1 D2 E 2 5 3 7 5 6 3 2 4 5 1 5 1 4 6 3 3 3 3 4 状态A 决策 阶段1 状态B1 阶段2 决策 状态C 状态D1 3 阶段3 决策 阶段4 决策 状态E 行程1 行程2 行程3 行程4

§2最优化原理与动态规划的数学模型 动态规划问题的解题思路 ◆动态规划的基本概念 ◆最优化原理与动态规划的数学模型 ◆逆序解法与顺序解法 ◆动态规划模型的分类 2014-12-15 4
2014-12-15 4 §2 最优化原理与动态规划的数学模型 动态规划问题的解题思路 动态规划的基本概念 最优化原理与动态规划的数学模型 逆序解法与顺序解法 动态规划模型的分类
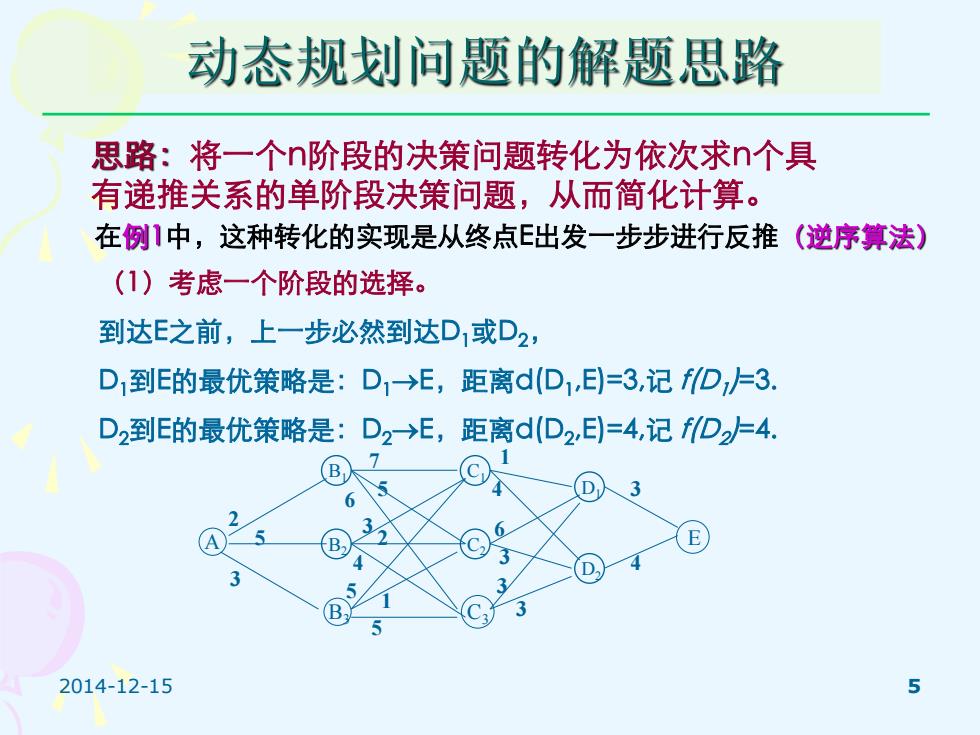
动态规划问题的解题思路 思路:将一个n阶段的决策问题转化为依次求n个具 有递推关系的单阶段决策问题,从而简化计算。 在例1中,这种转化的实现是从终点E出发一步步进行反推(逆序算法) (1)考虑一个阶段的选择。 到达E之前,上一步必然到达D1或D2, D,到E的最优策略是:D1→E,距离d(D1,E)=3,记fD=3. D2到E的最优策略是:D2→E,距离d(D2,E)=4,记f/D=4. B B 2014-12-15 5
2014-12-15 5 动态规划问题的解题思路 思路:将一个n阶段的决策问题转化为依次求n个具 有递推关系的单阶段决策问题,从而简化计算。 在例1中,这种转化的实现是从终点E出发一步步进行反推(逆序算法) (1)考虑一个阶段的选择。 到达E之前,上一步必然到达D1或D2, D1到E的最优策略是:D1E,距离d(D1 ,E)=3,记 f(D1 )=3. D2到E的最优策略是:D2E,距离d(D2 ,E)=4,记 f(D2 )=4. 1 A B1 B2 B3 C3 C2 C1 D1 D2 E 2 5 3 7 5 6 3 2 4 5 1 5 4 6 3 3 3 3 4