
第二章线性规划的对偶理论 本章主要内容: ·对偶问题的提出 原问题与对偶问题 ◆对偶问题的基本性质 ◆对偶的经济解释 —影子价格 对偶单纯形法 灵敏度分析 2014-12-15
2014-12-15 1 第二章 线性规划的对偶理论 对偶问题的提出 原问题与对偶问题 对偶问题的基本性质 对偶的经济解释——影子价格 对偶单纯形法 灵敏度分析 本章主要内容:
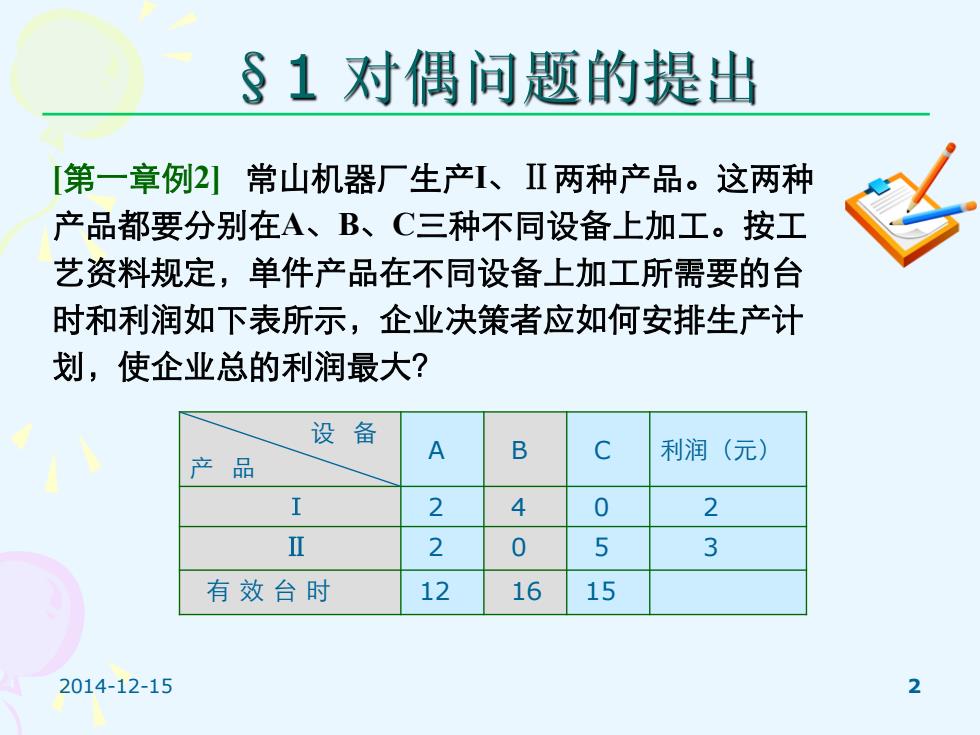
§1对偶问题的提出 第一章例2)常山机器厂生产1、Ⅱ两种产品。这两种 产品都要分别在A、B、C三种不同设备上加工。按工 艺资料规定,单件产品在不同设备上加工所需要的台 时和利润如下表所示,企业决策者应如何安排生产计 划,使企业总的利润最大? 设备 A B 利润(元) 产品 I 2 4 0 2 Ⅱ 2 0 5 3 有效台时 12 16 15 2014-12-15 2
2014-12-15 2 §1 对偶问题的提出 [第一章例2] 常山机器厂生产I、Ⅱ两种产品。这两种 产品都要分别在A、B、C三种不同设备上加工。按工 艺资料规定,单件产品在不同设备上加工所需要的台 时和利润如下表所示,企业决策者应如何安排生产计 划,使企业总的利润最大? 设 备 产 品 A B C 利润(元) I 2 4 0 2 Ⅱ 2 0 5 3 有 效 台 时 12 16 15

§1对偶问题的提出 解:设X、分别为、川两种产品的产量,则数学模型为: max Z=2x+3x2 2x1+2x2≤12 4x1 ≤16 (1) S.t. 5x2≤15 x1≥0,X2≥0 反过来问:现假定有另一四海机器厂,为扩大生产想租借常 山机器厂拥有的3种设备资源,问常山厂分别以每小时什么 样的价格才愿意出租自己的设备? 2014-12-15 3
2014-12-15 3 §1 对偶问题的提出 解:设x 1、x 2分别为I、Ⅱ两种产品的产量,则数学模型为: max Z = 2x1 + 3x2 x1 ≥ 0 , x2 ≥ 0 s.t. 2x1 + 2x2 ≤ 12 4x1 ≤ 16 5x2 ≤ 15 反过来问:现假定有另一四海机器厂,为扩大生产想租借常 山机器厂拥有的3种设备资源,问常山厂分别以每小时什么 样的价格才愿意出租自己的设备? (1)

§1对偶问题的提出 解:设A、B、C3种设备每小时出租的价格分别为y小、y2、 3,则新的线性规划数学模型为: min0=12y,+16y2+15y3 2y+42+0y3≥2 (2) s.t2y+0y2+5y3≥3 、y1,y2,y3≥0 任何一个线性规划问题都存在一个伴生的线性规划问题, 我们称之为“对偶”。 2014-12-15
2014-12-15 4 §1 对偶问题的提出 解:设A、B、C 3种设备每小时出租的价格分别为y1、y2、 y3,则新的线性规划数学模型为: , , 0 2 0 5 3 2 4 0 2 . . min 12 16 15 1 2 3 1 2 3 1 2 3 1 2 3 y y y y y y y y y st y y y (2) 任何一个线性规划问题都存在一个伴生的线性规划问题, 我们称之为“对偶”

§2原问题与对偶问题 把同种问题的两种提法所获得的数学模型写在一块,将会 发现一个有趣的现象。 max Z=2x+3x2 min0=12y+16y2+15y3 2X1+2x2≤12 2y+4y2+0y≥2 4x1 ≤16 (1) (2) s.t. st2y+0y2+5y3≥3 5x2≤15 y,y2,为3≥0 X1≥0,X2≥0 原问题 对偶问题 (对偶问题) (原问题) 称(2)为(1)的对偶,也称(1)为(2) 的对偶。 2014-12-15 5
2014-12-15 5 §2 原问题与对偶问题 称(2)为(1)的对偶,也称(1)为(2)的对偶。 , , 0 2 0 5 3 2 4 0 2 . . min 12 16 15 1 2 3 1 2 3 1 2 3 1 2 3 y y y y y y y y y st max Z = 2x1 + 3x2 y y y x1 ≥ 0 , x2 ≥ 0 s.t. 2x1 + 2x2 ≤ 12 4x1 ≤ 16 5x2 ≤ 15 (1) (2) 把同种问题的两种提法所获得的数学模型写在一块,将会 发现一个有趣的现象。 原问题 (对偶问题) 对偶问题 (原问题)