
第六章图与网络分析 本章主要内容: 图的基本概念与模型 兼树图与图的最小部分树 ◆最短路问题 幸网络的最大流 ◆最小费用流(略)》 2014-12-15 1
2014-12-15 1 第六章 图与网络分析 图的基本概念与模型 树图与图的最小部分树 最短路问题 网络的最大流 最小费用流(略) 本章主要内容:
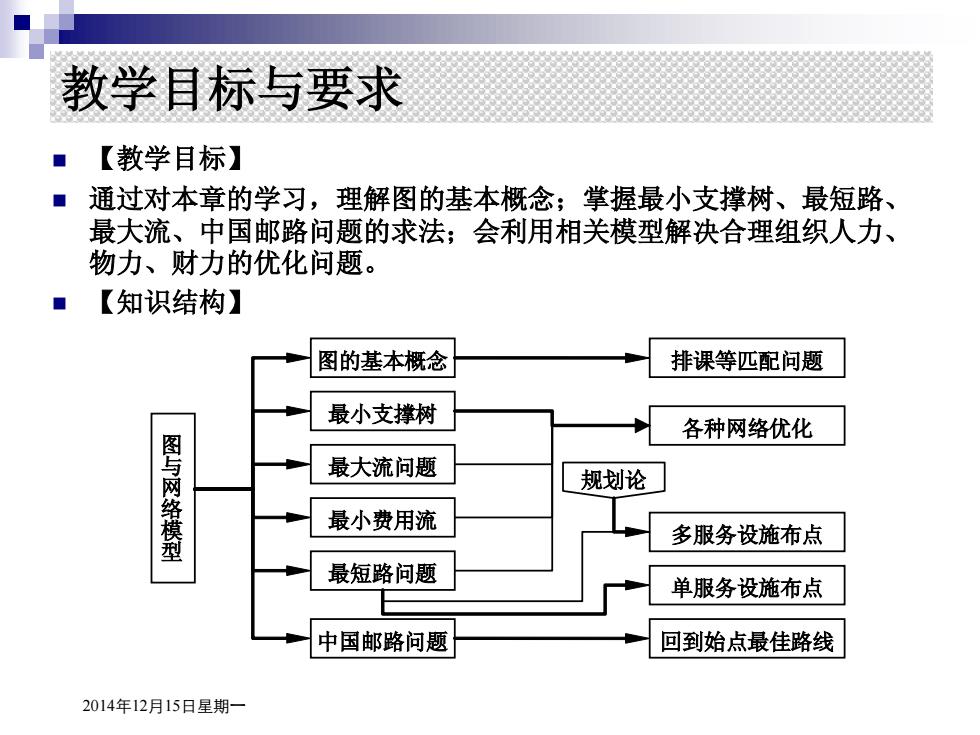
教学目标与要求 ■【教学目标】 ■通过对本章的学习,理解图的基本概念;掌握最小支撑树、最短路、 最大流、中国邮路问题的求法;会利用相关模型解决合理组织人力、 物力、财力的优化问题。 【知识结构】 图的基本概念 排课等匹配问题 最小支撑树 各种网络优化 图与网络模型 最大流问题 规划论 最小费用流 多服务设施布点 最短路问题 单服务设施布点 中国邮路问题 回到始点最佳路线 2014年12月15日星期一
2014年12月15日星期一 教学目标与要求 【教学目标】 通过对本章的学习,理解图的基本概念;掌握最小支撑树、最短路、 最大流、中国邮路问题的求法;会利用相关模型解决合理组织人力、 物力、财力的优化问题。 【知识结构】 图 与 网 络 模 型 图的基本概念 最大流问题 最小支撑树 最小费用流 排课等匹配问题 各种网络优化 回到始点最佳路线 最短路问题 中国邮路问题 多服务设施布点 单服务设施布点 规划论
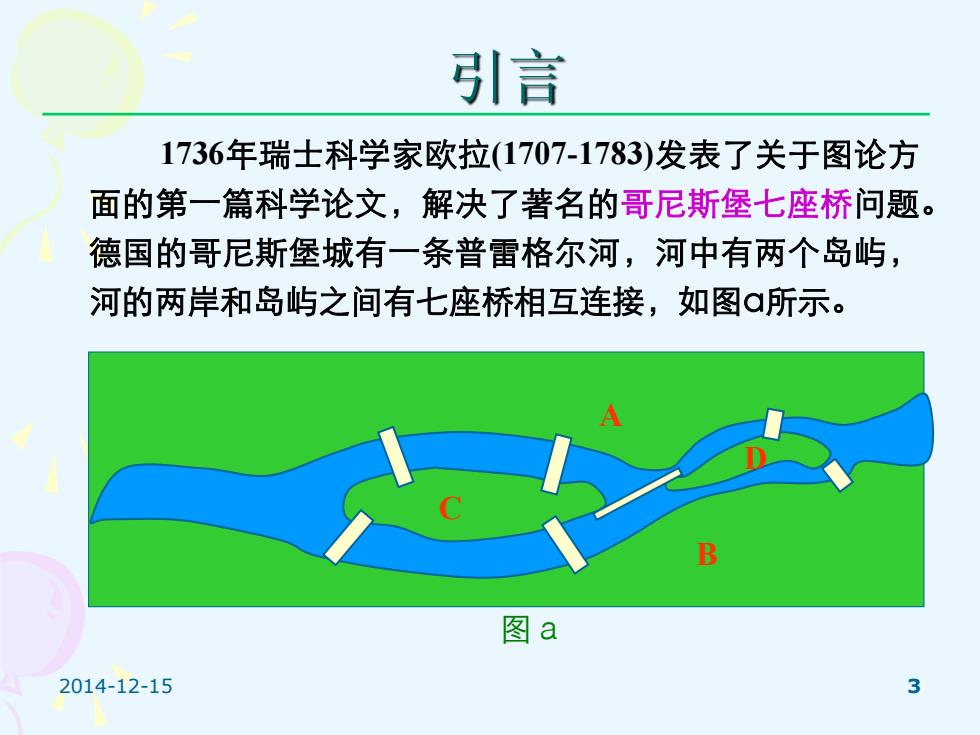
引言 1736年瑞士科学家欧拉(1707-1783)发表了关于图论方 面的第一篇科学论文,解决了著名的哥尼斯堡七座桥问题。 德国的哥尼斯堡城有一条普雷格尔河,河中有两个岛屿, 河的两岸和岛屿之间有七座桥相互连接,如图a所示。 B 图a 2014-12-15
2014-12-15 3 引言 1736年瑞士科学家欧拉(1707-1783)发表了关于图论方 面的第一篇科学论文,解决了著名的哥尼斯堡七座桥问题。 德国的哥尼斯堡城有一条普雷格尔河,河中有两个岛屿, 河的两岸和岛屿之间有七座桥相互连接,如图a所示。 B A C D 图a
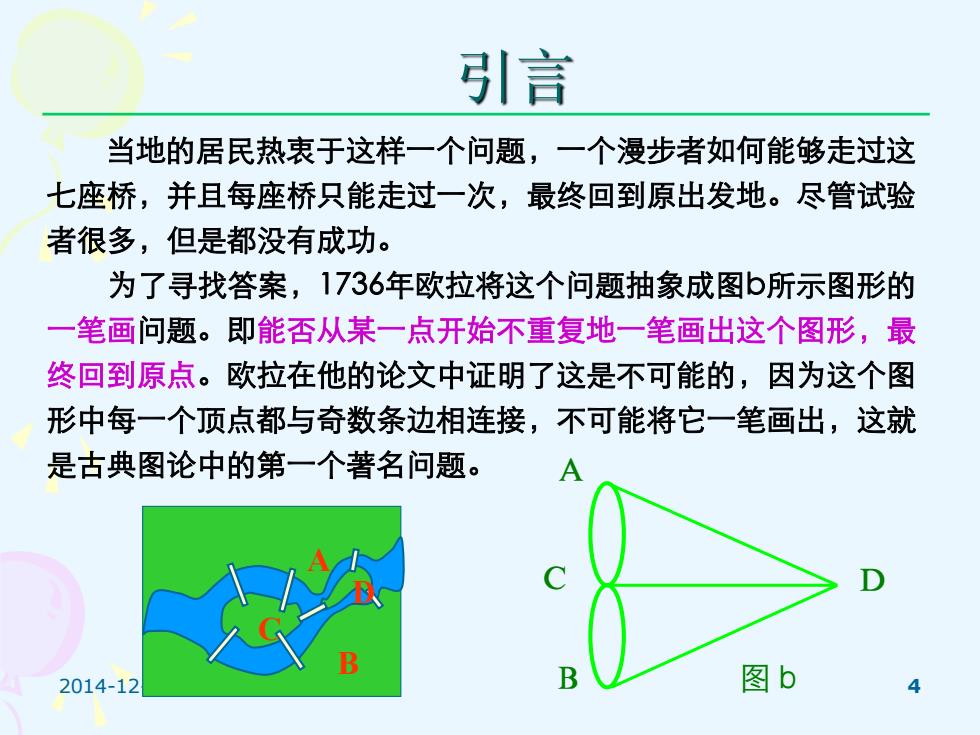
引言 当地的居民热衷于这样一个问题,一个漫步者如何能够走过这 七座桥,并且每座桥只能走过一次,最终回到原出发地。尽管试验 者很多,但是都没有成功。 为了寻找答案,1736年欧拉将这个问题抽象成图所示图形的 一笔画问题。即能否从某一点开始不重复地一笔画出这个图形,最 终回到原点。欧拉在他的论文中证明了这是不可能的,因为这个图 形中每一个顶点都与奇数条边相连接,不可能将它一笔画出,这就 是古典图论中的第一个著名问题。 A 2014-12 B 图b 4
2014-12-15 4 引言 当地的居民热衷于这样一个问题,一个漫步者如何能够走过这 七座桥,并且每座桥只能走过一次,最终回到原出发地。尽管试验 者很多,但是都没有成功。 为了寻找答案,1736年欧拉将这个问题抽象成图b所示图形的 一笔画问题。即能否从某一点开始不重复地一笔画出这个图形,最 终回到原点。欧拉在他的论文中证明了这是不可能的,因为这个图 形中每一个顶点都与奇数条边相连接,不可能将它一笔画出,这就 是古典图论中的第一个著名问题。 B A C D D A C B 图b

§1图的基本概念与模型 图的定义: 若用点表示研究的对象,用边表示这些对象之间的联系, 则图G可以定义为点和边的集合,记作: G=V,E 其中:V一点集E一边集 ※图G区别于几何学中的图。这里只关心图中有多少个点以 及哪些点之间有连线。 通常,我们把点与点之间不带箭头的线叫做边,带箭头的线叫做弧。 如果一个图是由点和边所构成的,那么称为无向图,如果一个图是由 点和弧所构成的,那么称为它为有向图,记作D(V,A,其中俵示 有向图D的点集合,A表示有向图D的弧集合。一条方向从%指向y 的边和弧,分别记作[y,(。 2014-12-15
2014-12-15 5 §1 图的基本概念与模型 图的定义: 若用点表示研究的对象,用边表示这些对象之间的联系, 则图G可以定义为点和边的集合,记作: G {V , E} 其中: V——点集 E——边集 ※ 图G区别于几何学中的图。这里只关心图中有多少个点以 及哪些点之间有连线。 通常,我们把点与点之间不带箭头的线叫做边,带箭头的线叫做弧。 如果一个图是由点和边所构成的,那么称为无向图,如果一个图是由 点和弧所构成的,那么称为它为有向图,记作D=(V,A),其中V表示 有向图D的点集合,A表示有向图D的弧集合。一条方向从vi , 指向vj 的边和弧,分别记作[vi ,vj ],(vi ,vj )