3.基本回路 ·连通图的一个树包含全部结点 又不形成回路。 2 可见对任意一个树,加入一个 连支便形成一个回路。 4 >这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 3 >由全部连支形成的单连支回 路构成基本回路组。 16
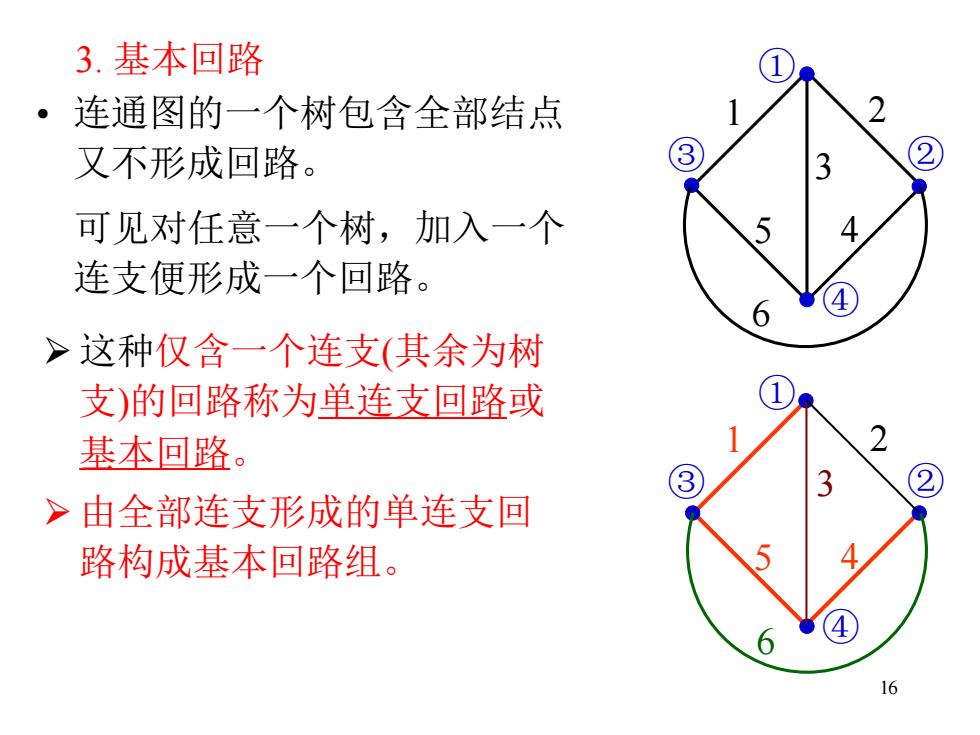
16 3. 基本回路 • 连通图的一个树包含全部结点 又不形成回路。 可见对任意一个树,加入一个 连支便形成一个回路。 ➢ 这种仅含一个连支(其余为树 支)的回路称为单连支回路或 基本回路。 ➢ 由全部连支形成的单连支回 路构成基本回路组。 ① ③ ② ④ 1 2 3 5 4 6 ① ③ ② ④ 1 5 4 2 6 3
因为每个基本回路包含了一条其他回路所没 有的支路,所以基本回路组是独立回路组。 >独立回路数等于连支数。 若一个连通图G有n个结点,b条支路, G的任一个树的树支数为(n-1), 连支数为b-(n-l), 则独立回路数1=b-(n-1)。 2 选择不同的 树,获得的 基本回路组 也不同。 17
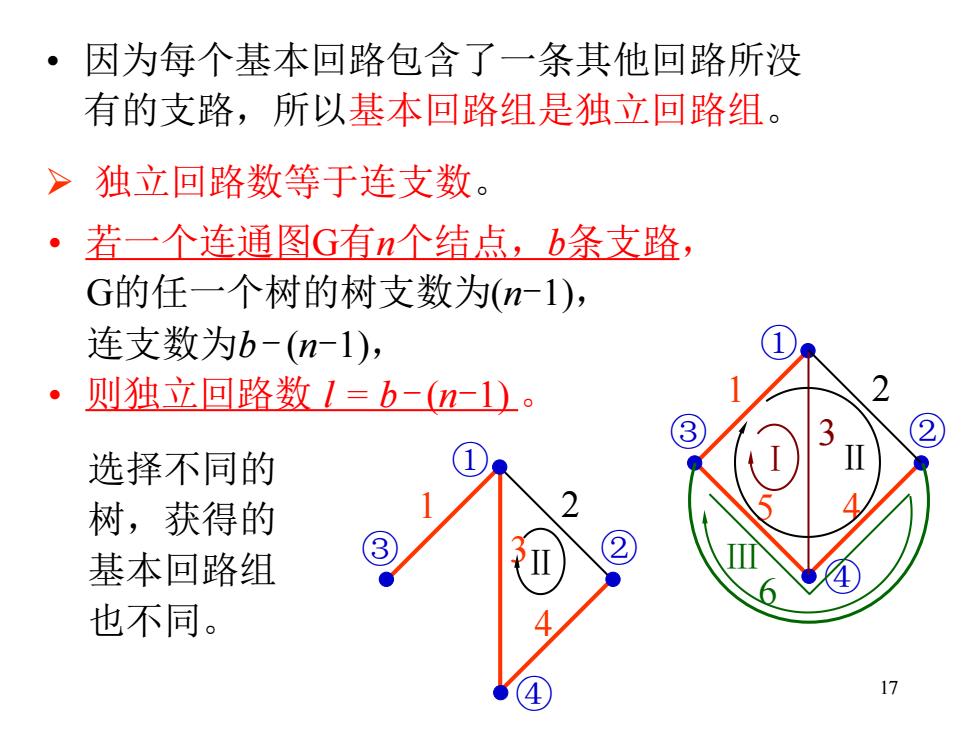
17 2 ➢ 独立回路数等于连支数。 • 因为每个基本回路包含了一条其他回路所没 有的支路,所以基本回路组是独立回路组。 • 若一个连通图G有n个结点,b条支路, G的任一个树的树支数为(n-1), 连支数为b- (n-1), • 则独立回路数 l = b- (n-1) 。 ① ③ ② ④ 1 5 4 2 6 3 Ⅰ Ⅱ Ⅲ 选择不同的 树,获得的 基本回路组 也不同。 ① ③ ② ④ 1 4 3Ⅱ
若把一个图画在平面上,能使它的各条支路除所连 接的结点外不再交叉,则这样的图称为平面图。 ·平面图的全部网 孔就是一组独立 回路。 。其数目恰好是该 图的独立回路数 非平面图 1=b-(n-1) >一个电路的KVL的独立方程 数等于它的独立回路数
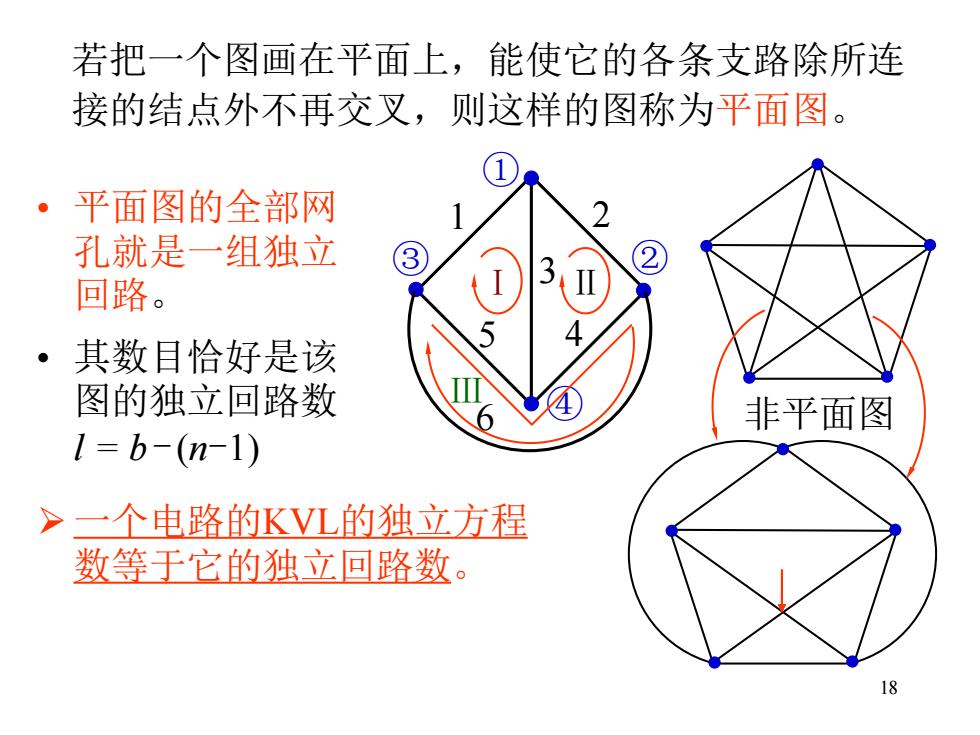
18 若把一个图画在平面上,能使它的各条支路除所连 接的结点外不再交叉,则这样的图称为平面图。 • 平面图的全部网 孔就是一组独立 回路。 • 其数目恰好是该 图的独立回路数 l = b- (n-1) ➢ 一个电路的KVL的独立方程 数等于它的独立回路数。 ① ③ ② ④ 1 2 3 5 4 6 非平面图 Ⅰ Ⅱ Ⅲ
KVL的独立方程组 ▣路I:u1+3+u5=0 ▣路IⅡ:u12+u4+u5=0 回路Ⅲ: -4-45+u6=0 若按网孔,则回路I、 I的方程不变, 回路Ⅲ的方程修改为: 2 -u2-3+u4=0 19
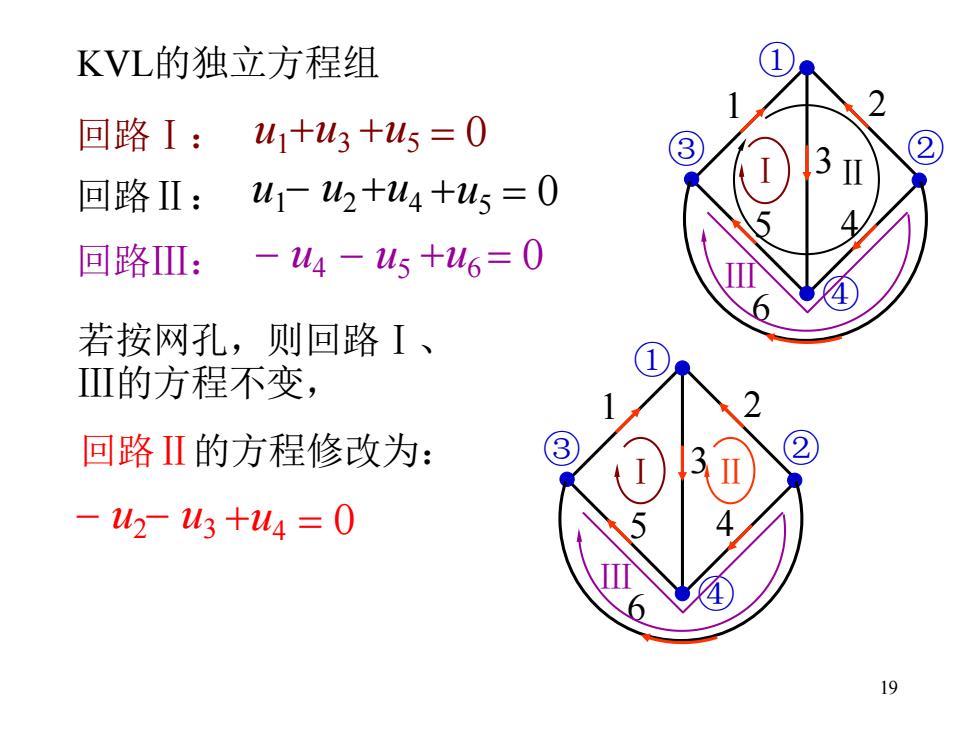
19 KVL的独立方程组 Ⅰ Ⅱ Ⅲ ① ③ ② ④ 1 2 3 5 4 6 回路Ⅰ: u1+u3 +u5 = 0 回路Ⅱ: u1- u2+u4 +u5 = 0 回路Ⅲ: - u4 - u5 +u6 = 0 若按网孔,则回路Ⅰ、 Ⅲ的方程不变, 回路Ⅱ的方程修改为: - u2 Ⅰ Ⅲ ① ③ ② ④ 1 2 3 5 4 6 Ⅱ - u3 +u4 = 0
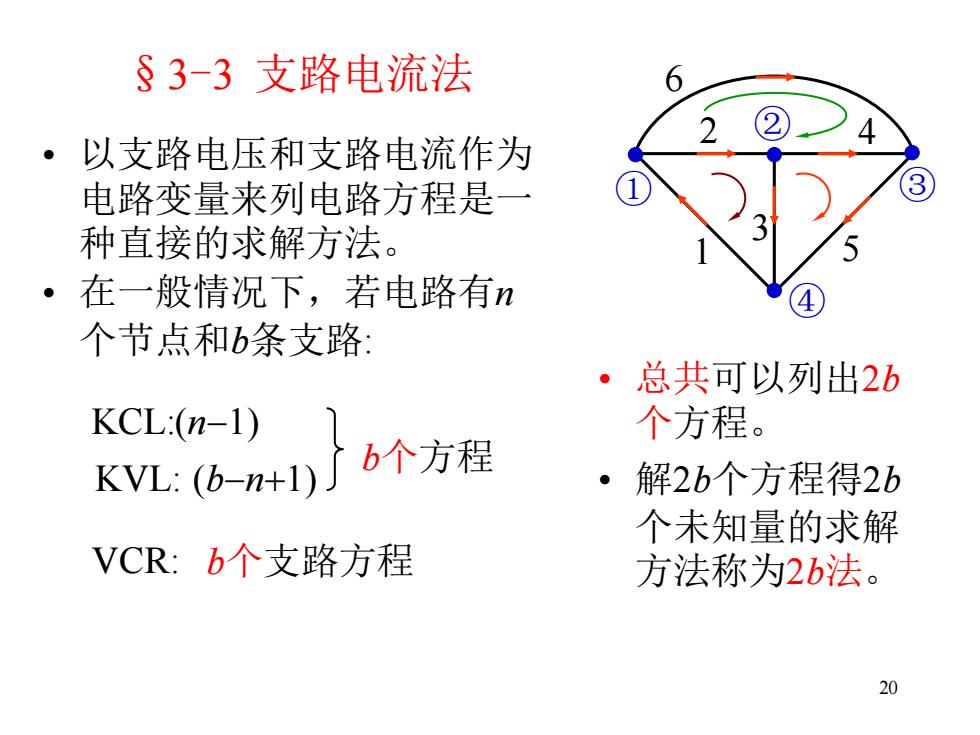
§3-3支路电流法 6 ·以支路电压和支路电流作为 电路变量来列电路方程是一 种直接的求解方法。 在一般情况下,若电路有n 个节点和b条支路: ·总共可以列出2b KCL:(n-1) 个方程。 KVL:(b-n+1) b个方程 ·解2b个方程得2b 个未知量的求解 VCR:b个支路方程 方法称为2b法。 20
20 §3-3 支路电流法 • 以支路电压和支路电流作为 电路变量来列电路方程是一 种直接的求解方法。 • 在一般情况下,若电路有n 个节点和b条支路: • 总共可以列出2b 个方程。 • 解2b个方程得2b 个未知量的求解 方法称为2b法。 ① ③ ② ④ 1 2 3 4 5 6 KCL:(n-1) b个方程 VCR: b个支路方程 KVL: (b-n+1)