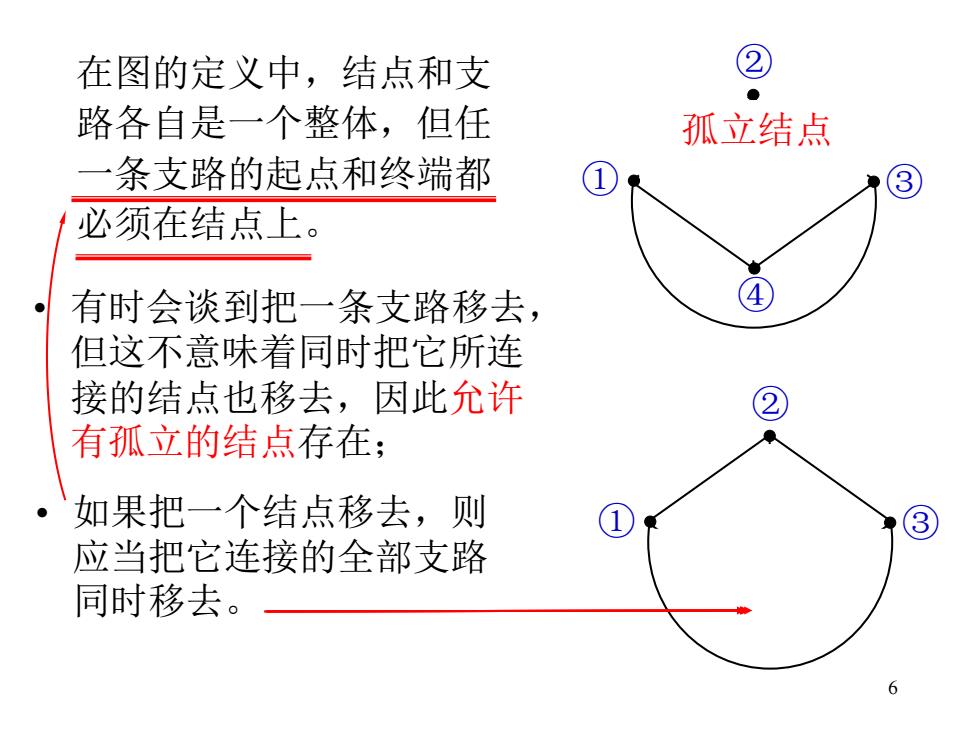
在图的定义中,结点和支 ② ● 路各自是一个整体,但任 孤立结点 一条支路的起点和终端都 ③ 必须在结点上。 有时会谈到把一条支路移去, ④ ● 但这不意味着同时把它所连 接的结点也移去,因此允许 ② 有孤立的结点存在; 。 如果把一个结点移去,则 应当把它连接的全部支路 同时移去。 6
6 在图的定义中,结点和支 路各自是一个整体,但任 一条支路的起点和终端都 必须在结点上。 • 有时会谈到把一条支路移去, 但这不意味着同时把它所连 接的结点也移去,因此允许 有孤立的结点存在; • 如果把一个结点移去,则 应当把它连接的全部支路 同时移去。 ① ② ③ ④ 孤立结点 ① ② ③ ④

可见,图论中关于支路和 结点的概念与电路中由具 体元件构成的支路以及结 ③ 点有些差别: 支路是实体 在电路中 4④) 结点由支路汇集而形成。 。 若对图的每一条支路也指定一个方向,此方向 即该支路电流(和电压)的参考方向。 ·支路均赋以方向的图,称为有向图。 ·支路未赋以方向的图,称为无向图。 7
7 可见,图论中关于支路和 结点的概念与电路中由具 体元件构成的支路以及结 点有些差别: • 若对图的每一条支路也指定一个方向,此方向 即该支路电流(和电压)的参考方向。 • 支路均赋以方向的图,称为有向图。 • 支路未赋以方向的图,称为无向图。 结点由支路汇集而形成。 支路是实体 ① ② ③ 在电路中 ④

本章的重点和难点 重点 用观察法,熟练应用支路电流法,回路电流法,结点电压法 的“方程通式”写出支路电流方程,回路电流方程,结点电 压方程,并求解。 难点 1.独立回路的确定 2.正确理解每一种方法的依据 3.含独立电流源和受控电流源的电路的回路电流方程的列写 4.含独立电压源和受控电压源的电路的结点电压方程的列写 8
8 本章的重点和难点 重点 用观察法,熟练应用支路电流法,回路电流法,结点电压法 的“方程通式”写出支路电流方程,回路电流方程,结点电 压方程,并求解。 难点 1. 独立回路的确定 2. 正确理解每一种方法的依据 3. 含独立电流源和受控电流源的电路的回路电流方程的列写 4. 含独立电压源和受控电压源的电路的结点电压方程的列写
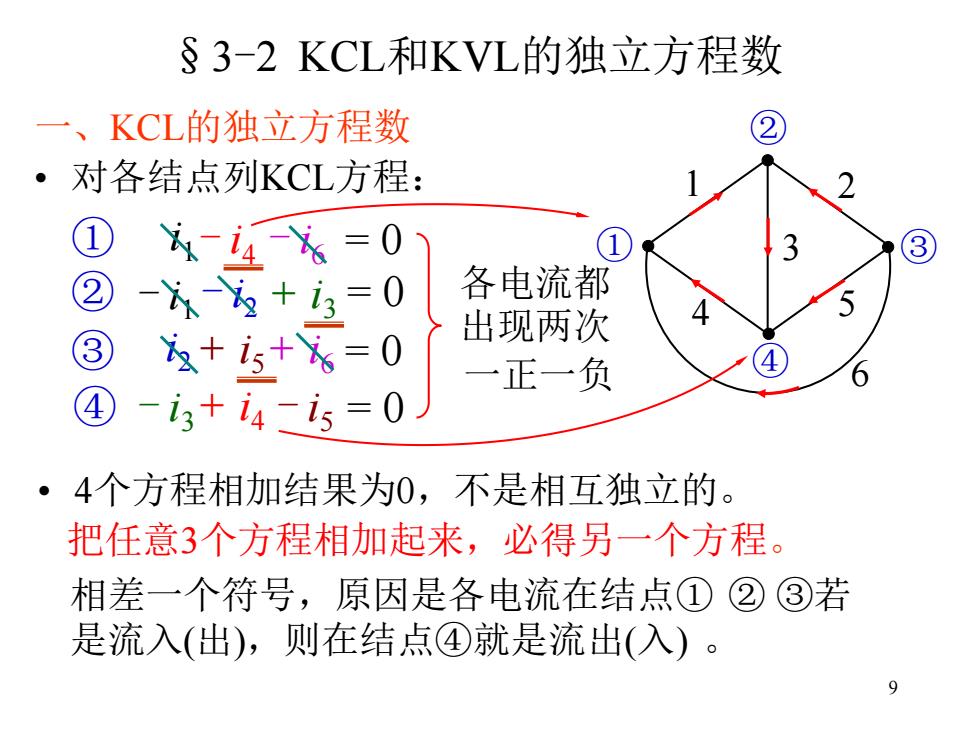
§3-2KCL和KVL的独立方程数 一、KCL的独立方程数 。 对各结点列KCL方程: ① ② 各电流都 出现两次 3) +i5+ =0 一正一负 4 -i3+i4-i5 =0 。 4个方程相加结果为0,不是相互独立的。 把任意3个方程相加起来,必得另一个方程。 相差一个符号,原因是各电流在结点①②③若 是流入(出),则在结点④就是流出(入)。 9
9 §3-2 KCL和KVL的独立方程数 • 4个方程相加结果为0,不是相互独立的。 一、KCL的独立方程数 • 对各结点列KCL方程: ① ② ③ ④ 1 2 3 4 5 6 ① i1- i4 - i6 = 0 ② - i1 - i2 + i3= 0 ③ i2 + i5+ i6= 0 ④ - i3+ i4 - i5 = 0 各电流都 出现两次 一正一负 把任意3个方程相加起来,必得另一个方程。 相差一个符号,原因是各电流在结点① ② ③若 是流入(出),则在结点④就是流出(入)

上述4个方程中,任意3个是独立的。 >对具有n个结点的电路,独立的KCL方程为任意 的(n-1)个。 与独立方程对应的结点叫做独立结点。 二、KVL的独立方程数 ·与KVL的独立方程对应的回路称独立回路。 因此,要列出KVL的独立方程组,首先要找出与之 对应的独立回路组。 ·有时,寻找独立回路组不是一件容易的事。利用 “树”的概念会有助于寻找一个图的独立回路组。 回路和独立回路的概念与支路的方向无关,现用无 向图介绍如下: 10
10 上述4个方程中,任意3个是独立的。 ➢ 对具有n个结点的电路,独立的KCL方程为任意 的(n-1)个 。 与独立方程对应的结点叫做独立结点。 二、 KVL的独立方程数 • 与KVL的独立方程对应的回路称独立回路。 因此,要列出KVL的独立方程组,首先要找出与之 对应的独立回路组。 • 有时,寻找独立回路组不是一件容易的事。利用 “树”的概念会有助于寻找一个图的独立回路组。 回路和独立回路的概念与支路的方向无关,现用无 向图介绍如下: