中国地质大学（武汉）：《数字信号处理》课程教学资源（课件讲稿）第七章 FIR数字滤波器的设计方法

2)n)奇对称 h(n)=-h(N-1-n) ◆频率响应： e=-en[-小] W-1N-1 相位函数： 0(o)1 N-1 π 0+ π 2 2 π 2π 为第二类线性相位 W-1 T= B。=π12 2 N

 频率响应： h n h N n ( ) ( 1 )     1 1 2 0 1 ( ) ( ) ( )sin 2 j N N j j z e n N H e H z je h n n                           1 2 N    1 1 2 2 0 1 ( )sin 2 N N j j n N e h n n                         0    / 2 2）h(n)奇对称 1 ( ) 2 2 N         相位函数： 为第二类线性相位

N-1 3、幅度函数的特点 偶对称中心 h() N=11 1)h(n)偶对称，N为奇数 n 幅度函数： 10 V-1 toynun n=0 -w--a-） cos 2粉 .cos

3、幅度函数的特点 1）h(n)偶对称，N为奇数 1 1 cos ( 1 ) cos 2 2 N N N n n                                  1 1 cos 2 2 N N n                  对 呈偶对称 1 0 1 ( ) ( )cos 2 N n N H h n n                     幅度函数： 1 cos 2 N n                

N-3 --咖小 n=0 N-1 -n=m 2 N-1 -4言ww N-1 N-1 2 Hlo)-a(n)cos(on） 偶对称中心 h(n) N=11 n=0 中：0=2 10 N-1 a0=2 N-1

-3 2 0 1 1 ( ) 2 ( )cos 2 2 N n N N H h h n n                            1 2 1 1 1 2 cos( ) 2 2 N m N N h h m m                     1 2 N n m  令   1 2 0 ( ) ( )cos( ) N n H a n n        1 (0) 2 N a h        其中： 1 1,..., 2 N n   1 ( ) 2 2 N a n h n         

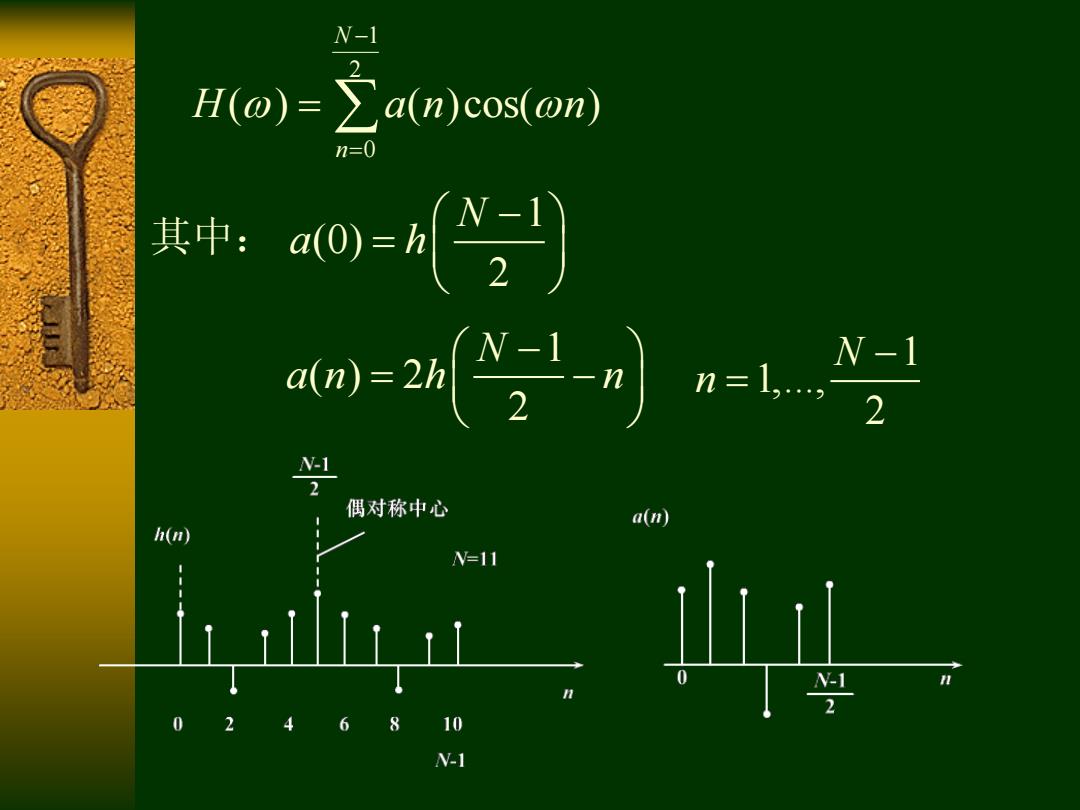
N-1 H(o)=∑a(n)cos(on) n=0 中：a0= n=1 N-1 2 偶对称中心 a() h(m) N=11 入了、 -1 2 6 8 10 N-1

1 2 0 ( ) ( )cos( ) N n H a n n       1 (0) 2 N a h        1 1,..., 2 N n   其中： 1 ( ) 2 2 N a n h n         

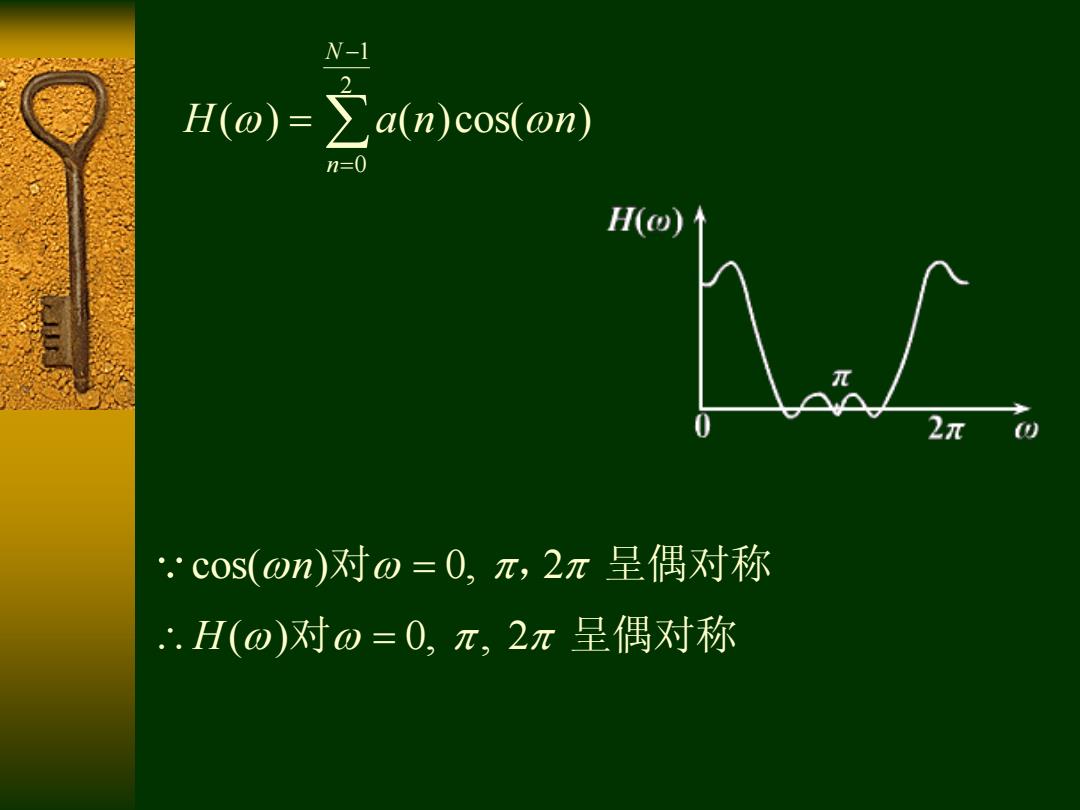
N-1 Ho)=∑am)cs(om) n=0 H(@) 2π .cos(on)对o=0,π，2π呈偶对称 ∴.H(O)对0=0，π，2π呈偶对称

  H( ) 0, , 2     对 呈偶对称 cos( ) 0, 2     n 对 ， 呈偶对称  1 2 0 ( ) ( )cos( ) N n H a n n      