第一部分电力系统稳态分析 第三章简单电力系统的分析和计算 一、基本要求 掌握电力线路中的电压降落和功率损耗的计算、变压器中的电压降落和功率损耗的计 算:掌握辐射形网络的潮流分布计算:掌握简单环形网络的潮流分布计算:了解电力网络 的简化。 二、重点内容 1、电力线路中的电压降落和功率损耗 图3-1中,设线路末端电压为心2、末端功率为5,=B+j02,则 (1)计算电力线路中的功率损耗 ①线路末端号纳支路的功率损耗:A:-得)=寸咀 .(3-1 则阻抗支路末端的功率为:=32+△了, ②线路阻抗支路中的功率损耗: A5,=1P2=+R+x))(3-2 U 则阻抗支路始端的功率为:=;+△S2 ③线路始端导纳支路的功率损耗: (3-3) 则线路始端的功率为: S=+A5 R+X 4父 d心 S ↓52 (2)计算电力线路中的电压降落 选取心2为参考向量,如图3-2。线路始端电压U,=U2+△U+j6U 其中 AU-ER+OX X-OR .(3-4) 11
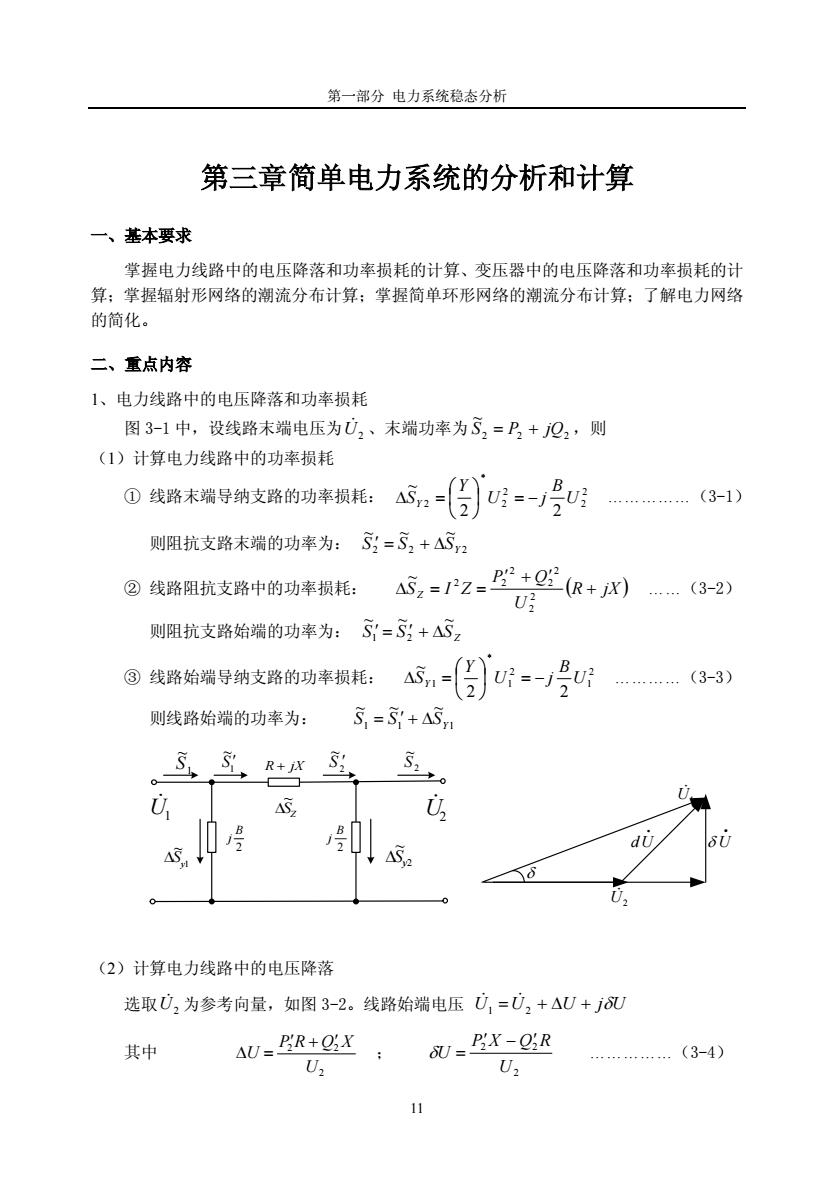
第一部分 电力系统稳态分析 第三章 简单电力系统的分析和计算 一、 基本要求 掌握电力线路中的电压降落和功率损耗的计算、变压器中的电压降落和功率损耗的计 算;掌握辐射形网络的潮流分布计算;掌握简单环形网络的潮流分布计算;了解电力网络 的简化。 二、 重点内容 1、电力线路中的电压降落和功率损耗 图 3-1 中,设线路末端电压为U& 2 、末端功率为 2 2 2 ~ S = P + jQ ,则 (1)计算电力线路中的功率损耗 ① 线路末端导纳支路的功率损耗: 2 2 2 2 * 2 2 2 ~ UB U j Y SY ⎟ = − ⎠ ⎞ ⎜ ⎝ ⎛ ∆ = .(3-1) 则阻抗支路末端的功率为: 2 2 2 ~ ~ ~ Y S ′ = S + ∆S ② 线路阻抗支路中的功率损耗: (R jX U P Q S Z I Z + ′ + ′ ∆ = = 2 2 2 2 2 ~ 2 2 ) .(3-2) 则阻抗支路始端的功率为: Z S S S ~ ~ ~ 1 ′ = 2 ′ + ∆ ③ 线路始端导纳支路的功率损耗: 2 1 2 1 * 1 2 2 ~ UB U j Y SY ⎟ = − ⎠ ⎞ ⎜ ⎝ ⎛ ∆ = .(3-3) 则线路始端的功率为: 1 1 1 ~ ~ ~ Y S = S ′ + ∆S δ U2 & U1 & • dU • δ U U1 & U2 & 1 ~ S 2 ~ S 1 ~ S ′ 2 ~ S ′ 1 ~ y ∆S 2 ~ ∆Sy SZ ~ ∆ R + jX 2 B j 2 Bj (2)计算电力线路中的电压降落 选取 为参考向量,如图 3-2。线路始端电压 U2 & U& 1 =U& 2 + ∆U + jδU 其中 2 2 2 U P R Q X U ′ + ′ ∆ = ; 2 2 2 U P X Q R U ′ − ′ δ = .(3-4) 11

电力系统分析学习指导与习题集 则线路始端电压的大小: U=(U2+AU)+(8U) .(3-5) 一般可采用近似计算: UU:+AU=U,+BR+0X (3-6) U、 2、变压器中的电压降落和电能损耗 图3-3中,设变压器末端电压为心2、末端功率为S2=D,+jQ2,则 03 (1)计算变压器中的功率损耗 ①变压器阻抗支路的功率损耗: A=Pz,=+9R+x) U及 .(3-7) 则变压器阻抗支路始端的功率为:=了,+△S, ②变压器导纳支路的功率损耗: △3n=YU=(G,+jB,)U .(3-8) 则变压器始端的功率为: S1=S+ASm。 (2)计算变压器中的电压降落 变压器始端电压: U=U,+AU,+jou, 其中 A,-EkOX.w-Bx-QR .(3-9 U 则变压器始端电压的大小:U,=√心,+△U,)}+(6U,P .(3-10) 一般可采用近似计图33变崖器的电压和功率 .(3-11) 3、辐射形网络潮流计算 潮流(power flow)计算是指电力网络中各节点电压、各元件流过的电流或功率等的计 算
电力系统分析学习指导与习题集 则线路始端电压的大小: ( ) ( ) 2 2 U1 = U2 + ∆U + δU .(3-5) 一般可采用近似计算: 2 2 2 1 2 2 U P R Q X U U U U ′ + ′ ≈ + ∆ = + .(3-6) 2、变压器中的电压降落和电能损耗 图 3-3 中,设变压器末端电压为U& 2 、末端功率为 2 2 2 ~ S = P + jQ ,则 U1 & U2 & 1 ~ S 2 2 ~ ~ S′ = S ZT YT 1 ~ S ′ SyT ~ ∆ SZT ~∆ (1)计算变压器中的功率损耗 ① 变压器阻抗支路的功率损耗: ( ZT T T T R jX U P Q S I Z + + ∆ = = 2 2 2 2 2 ~ 2 2 ) .(3-7) 则变压器阻抗支路始端的功率为: ZT S S S ~ ~ ~ 1 ′ = 2 + ∆ ② 变压器导纳支路的功率损耗: ( * 2 YT 1 T T S Y U G ) 2 1 ∆ = % = + jB U .(3-8) 则变压器始端的功率为: YT S S S ~ ~ ~ 1 = 1 ′ + ∆ 。 (2)计算变压器中的电压降落 变压器始端电压: T UT U1 =U2 + ∆U + jδ & & 其中 2 2 2 U P R Q X U T T T + ∆ = , 2 2 2 U P X Q R U T T T − δ = .(3-9) 则变压器始端电压的大小: ( ) ( ) 2 2 U1 = U2 + ∆UT + δUT .(3-10) 2 2 2 1 2 2 U P R Q X U U U T T T + 一般可采用近似计算: U ≈ + ∆ = + .(3-11) 3、 辐射形网络潮流计算 潮流(power flow)计算是指电力网络中各节点电压、各元件流过的电流或功率等的计 算。 12

第一部分电力系统稳态分析 辐射形网络潮湖流计算主要有两种类型: (1)己知同一端点的电压和功率求潮流分布,采用逐段推算法: 逐段推算法:根据已知端点的电压和功率,逐段推算电网各点电压和功率。参看例3-1。 (2)己知不同端点的电压和功率求潮流分布,采用逐步渐进法。 逐步渐进法:首先设已知功率端点的电压为心©,运用该点已知的功率3和心推算 电网潮流:再由另一端点已知电压心,和求得的功率$四推算电网各点电压:以此类推,反 复推算,逐步逼近结果。 逐步渐进法的近似算法:首先设电网未知点的电压为U、,运用已知的功率计算电网功 率分布:再由另一端点已知电压U和求得的各点功率计算电网电压分布。参看例3-3。 4、环式网络的近似功率分布计算 将最简单的环式网络简化,并将电源节点一分为二得到等值环式网络的等值电路如图 3-4。其两端电压大小相等、相位相同。 2, 2 Z 图3-4等值环式网铬的等值电路 环式网络的近似功率分布: 2+2+3,2 5.=- (3-12) Z1+Z2+Z3 32i+,z+i2】 5,=2+z+2 .(3-13) 3a=3。-3 .(3-14) 5、两端供电网络的近似功率分布计算 将最简单的两端供电网络简化,得到两端供电网的等值电路如图3-5。其两端电压大小 不等、相位不同,1≠心
第一部分 电力系统稳态分析 辐射形网络潮流计算主要有两种类型: (1)已知同一端点的电压和功率求潮流分布,采用逐段推算法; 逐段推算法:根据已知端点的电压和功率,逐段推算电网各点电压和功率。参看例3-1 。 (2)已知不同端点的电压和功率求潮流分布,采用逐步渐进法。 逐步渐进法:首先设已知功率端点的电压为 ,运用该点已知的功率 和 推算 电网潮流;再由另一端点已知电压 和求得的功率 推算电网各点电压;以此类推,反 复推算,逐步逼近结果。 (0) Ui & i S & (0) Ui & U j & (1) S j & 逐步渐进法的近似算法:首先设电网未知点的电压为 ,运用已知的功率计算电网功 率分布;再由另一端点已知电压U 和求得的各点功率计算电网电压分布。参看例 3-3 。 U N 4、环式网络的近似功率分布计算 将最简单的环式网络简化,并将电源节点一分为二得到等值环式网络的等值电路如图 3-4。其两端电压大小相等、相位相同。 2 ~ S S a ~ S b ~ 3 ~ S 1 2 2 3 1′ Z 1 Z Z 3 23 ~ S 图 3-4 等值环式网络的等值电路 环式网络的近似功率分布: 3 * 2 * 1 * * 3 3 * 3 2 * 2 ~ ~ ~ Z Z Z S Z Z S Z Sa + + ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ + = .(3-12) 3 * 2 * 1 * * 2 1 * 3 * 2 1 ~ ~ ~ Z Z Z S Z S Z Z Sb + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = .(3-13) 23 2 ~ ~ ~ S S S = a − .(3-14) 5、两端供电网络的近似功率分布计算 将最简单的两端供电网络简化,得到两端供电网的等值电路如图 3-5。其两端电压大小 不等、相位不同, 。 U1 U4 & & ≠ 13

电力系统分析学习指导与习题集 Sc Z 图35两端供电网的等值电路 由于两端电压U,≠04,它们之间存在相量差d心=U1-U4,就使得由节点1到节 点4产生了一个循环功率,以表示 循环功率 UxdU .(3-15) Z1+Z2+Z3 两端供电网络中,各线路中流过的功率可以看作是两个功率分量的叠加。其一为两端 电压相等时的环式网络的近似功率;另一为循环功率(注意循环功率的方向与d心的取向 有关)。两端供电网络的近似功率分布: 2+2,+3,2, 5,=- + 21+z+2 .(3-16) 乙+32+z】 3= -3 .(3-17) Z1+Z2+Z3 5=5,-3 .(3-18) 由此可见,区域性开式网络与区域性闭式网络在计算上的不同点就在于功率分布的计 算,后者的功率分布是分两步完成的。 当网络各线段的R值相等时,称之为均一网络。这类网络在不计功率损耗影响时, 自然功率分布的有功分量和无功分量是互不影响的。这时,他们是按电阻或电抗分布的, 即 a-iee 0.-i0R .(3-19) g豆, (3-18) R g,=0 R 将式(3-18)中的电阻换为相应的电抗也是正确的,特别是全网导线截面相同时,功
电力系统分析学习指导与习题集 14 2 ~ S S a ~ S b ~ 3 ~ S 1 2 2 3 4 Z 1 Z Z 3 23 ~ S S C ~ 图 3-5 两端供电网的等值电路 由于两端电压U1 ≠ U4 & & ,它们之间存在相量差 1 dU = U −U4 & & & ,就使得由节点 1 到节 点 4 产生了一个循环功率,以 CS 表示 循环功率 3 * 2 * 1 * * ~ Z Z Z U d U S N c + + = .(3-15) 两端供电网络中,各线路中流过的功率可以看作是两个功率分量的叠加。其一为两端 电压相等时的环式网络的近似功率;另一为循环功率(注意循环功率的方向与 的取向 有关)。两端供电网络的近似功率分布: dU& a c S Z Z Z S Z Z S Z S ~ ~ ~ ~ 3 * 2 * 1 * * 3 3 * 3 2 * 2 + + + ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ + = .(3-16) b c S Z Z Z S Z S Z Z S ~ ~ ~ ~ 3 * 2 * 1 * * 2 1 * 3 * 2 1 − + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = .(3-17) 23 2 ~ ~ ~ S S S = a − .(3-18) 由此可见,区域性开式网络与区域性闭式网络在计算上的不同点就在于功率分布的计 算,后者的功率分布是分两步完成的。 当网络各线段的 R/X 值相等时,称之为均一网络。这类网络在不计功率损耗影响时, 自然功率分布的有功分量和无功分量是互不影响的。这时,他们是按电阻或电抗分布的, 即 1 n i iB i A PR P R = Σ Σ = 1 n i iB i A Q R Q R = Σ Σ = .(3-19) 1 n i iA i B PR P R = Σ Σ = 1 n i iA i A Q R Q R = Σ Σ = .(3-18) 将式(3-18)中的电阻换为相应的电抗也是正确的,特别是全网导线截面相同时,功

第一部分电力系统稳态分析 率的自然分布按长度分布,即 54 1 5 1 .(3-19) 应该注意:环流高鼓功率的计算与网络是否均一无关。 可以证明:在闭式电力网络中,欲使有功功率损耗最小,应使功率分布按电阻分布, 即: 5-S .(3-20) R R 由此可见:均一网络功率的自然分布也就是有功损耗最小时的分布。因此,在进行网 络规划设计时,应使网络接近均一。对于非均一网络,要达此目的,必须采用一定的措施。 6、地方电力网络的计算 电压为35kV及以下的网络称为地方电力网。这种电力网由于其自身的特点(电压 较,线路较短,传输功率相对较小,等等),在计算时可大大简化。一般可作如下简化: ā、可不计线路电容的影响,线路的等值电路仅为一个串联阻抗: b、计算功率分布和电压分布时,可不计功率损耗的影响,并用网络额定电压: c、计算电压分布时,可不计电压降落横分量(这对11OkV网络同样适用),这时, 电压降落纵分量近似等于电压损耗,即 △V≈↓2(PR,+0,X,)*52u,cosp,R+1,sin9,X,) VN 式中P,Q,-通过线段j负荷功率的有功分量((real power component)和无功分量 (reactive power component); R,X,-线段j的电阻和电抗 I,cosp,-流过线段j的负荷电流及功率因数(power factor) Vw-网络额定电压(rated voltage)) n-计算网络的线段数 d、有的线段具有较均匀分布的负荷,计算时可用一个集中负荷来代替,其大小等 于均匀分布负荷的总和,其位置居均匀分布线段的中点,如图所示
第一部分 电力系统稳态分析 率的自然分布按长度分布,即 1 n iB i i A l l S S = Σ Σ = % % 1 n iA i i B l l S S = Σ Σ = % % .(3-19) 应该注意:环流高鼓功率的计算与网络是否均一无关。 可以证明:在闭式电力网络中,欲使有功功率损耗最小,应使功率分布按电阻分布, 即: 1 n iB i i A opt l R S S = ⋅ Σ Σ = % % 1 n iA i i B opt l R S S = ⋅ Σ Σ = % % .(3-20) 由此可见:均一网络功率的自然分布也就是有功损耗最小时的分布。因此,在进行网 络规划设计时,应使网络接近均一。对于非均一网络,要达此目的,必须采用一定的措施。 6、地方电力网络的计算 电压为 35kV 及以下的网络称为地方电力网。这种电力网由于其自身的特点(电压 较,线路较短,传输功率相对较小,等等),在计算时可大大简化。一般可作如下简化: a、 可不计线路电容的影响,线路的等值电路仅为一个串联阻抗; b、 计算功率分布和电压分布时,可不计功率损耗的影响,并用网络额定电压; c、 计算电压分布时,可不计电压降落横分量(这对 110kV 网络同样适用),这时, 电压降落纵分量近似等于电压损耗,即 ∑ ∑ = = ∆ ≈ + ≈ + n j j j j j j j n PjRj Qj X j I R I X N j 1 1 ( ) 3 ( cos sin ) V 1 V ϕ ϕ 式中 -通过线段 j 负荷功率的有功分量(real power component)和无功分量 (reactive power component ); Pj Qj Rj X j − − 线段 j 的电阻和电抗 I j cosϕ j − − 流过线段 j 的负荷电流及功率因数(power factor) VN − − 网络额定电压(rated voltage) n − − 计算网络的线段数 d、 有的线段具有较均匀分布的负荷,计算时可用一个集中负荷来代替,其大小等 于均匀分布负荷的总和,其位置居均匀分布线段的中点,如图所示。 15