§9-4自感应和互感应 一、 自感应 自感现象由于回 路中电流产生的磁通 量发生变化,而在自 己回路中激发感应电 动势的现象叫做自感 现象,这种感应电动 势叫做自感电动势。 让美觉返司退
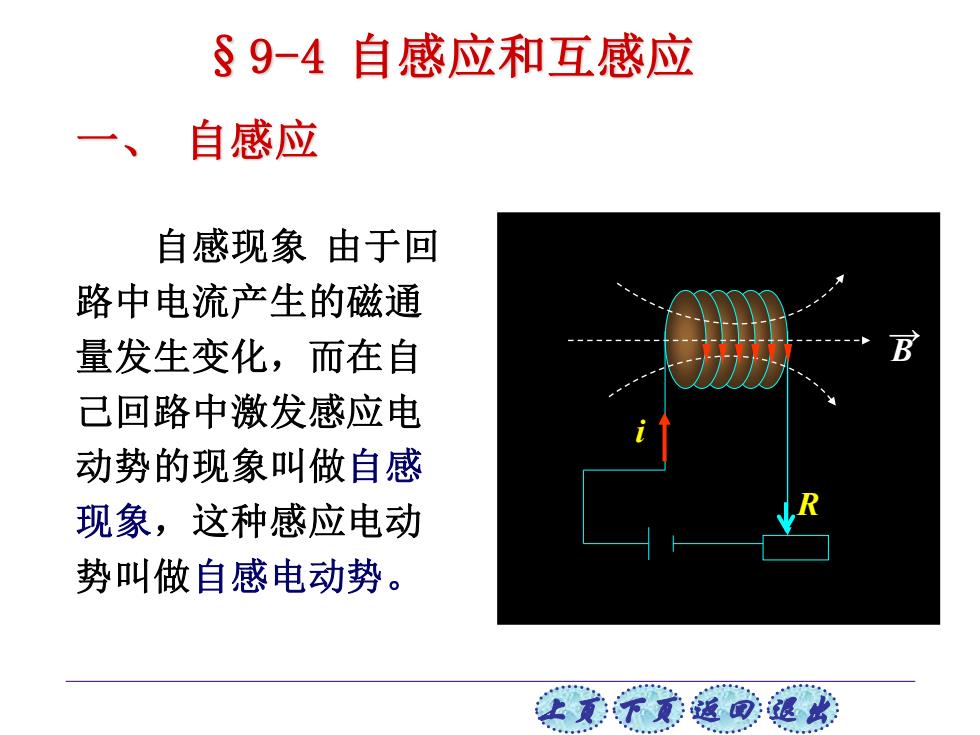
上页 下页 返回 退出 自感现象 由于回 路中电流产生的磁通 量发生变化,而在自 己回路中激发感应电 动势的现象叫做自感 现象,这种感应电动 势叫做自感电动势。 §9-4 自感应和互感应 一、 自感应 i R B →

设有一无铁芯的长直螺线管,长为1,截面半径 为R,管上绕组的总匝数为N,其中通有电流I。 因 B=4.W7 故 Φ=BS=NM πR2 1 穿过W匝线圈的磁链数为 Dy N=4oN2I 元R2 当线圈中的电流I发生变化时,在N匝线圈中产 生的感应电动势为 8L= d-4元fd- L-_L_Idi 三L d dt dt
上页 下页 返回 退出 设有一无铁芯的长直螺线管,长为 ,截面半径 为 ,管上绕组的总匝数为 ,其中通有电流 。 l R N I l NI B 0 = 0 2 πR l NI Φ BS = = 穿过 N 匝线圈的磁链数为 2 2 0 πR l N I ΦN NΦ = = 当线圈中的电流 发生变化时,在 匝线圈中产 生的感应电动势为 I N t I l R N t ΦN L d π d d d 2 2 0 = − = − t I L L d d = − 因 故

其中兀体现回路产生自感电动势来反抗电流改变 的能力,称为回路的自感系数,简称自感。它由回路 的大小、形状、匝数以及周围磁介质的性质决定。 对于一个任意形状的回路,回路中由于电流变 化引起通过回路本身磁链数的变化而出现的感应电 动势为 EL L=-L9 di dI dt 让美下觉返同速
上页 下页 返回 退出 t I L L d d = − 其中 体现回路产生自感电动势来反抗电流改变 的能力,称为回路的自感系数,简称自感。它由回路 的大小、形状、匝数以及周围磁介质的性质决定。 L 对于一个任意形状的回路,回路中由于电流变 化引起通过回路本身磁链数的变化而出现的感应电 动势为 t ΦN L d d = − t I L d d = − t I I ΦN d d d d = −

在上式中 L= dΦN dI 自感系数:等于回路中的电流变化为单位值时, 在回路本身所围面积内引起磁链数的改变值。 如果回路的几何形状保持不变,而且在它的周 围空间没有铁磁性物质。 在这种情况下,自感:回路自感的大小等于回路 中的电流为单位值时通过这回路所围面积的磁链数。 单位:H(亨利) 1H=1Wb.A- 1H=103mH=106uH 让贰子家返回退此
上页 下页 返回 退出 单位:H (亨利) 如果回路的几何形状保持不变,而且在它的周 围空间没有铁磁性物质。 I Φ L N = 在这种情况下,自感:回路自感的大小等于回路 中的电流为单位值时通过这回路所围面积的磁链数。 自感系数:等于回路中的电流变化为单位值时, 在回路本身所围面积内引起磁链数的改变值。 I Φ L N d d 在上式中 = 1 1H 1Wb A − = 1H 10 mH 10 μH 3 6 = =
例题9-7由两个“无限长”的同轴圆筒状导体所 组成的电缆,其间充满磁导率为4的磁介质,电缆 中沿内圆筒和外圆筒流过的电流I大小相等而方向 相反。设内外圆筒的半径分别为R和R,求电缆 单位长度的自感。 解:应用安培 环路定理,可知在内 圆筒之内以及外圆筒 之外的空间中磁感应 强度都为零。在内外 dr 两圆筒之间,离开轴 线距离为”处的磁感 B 应强度为 2元r 上文不美返回退球
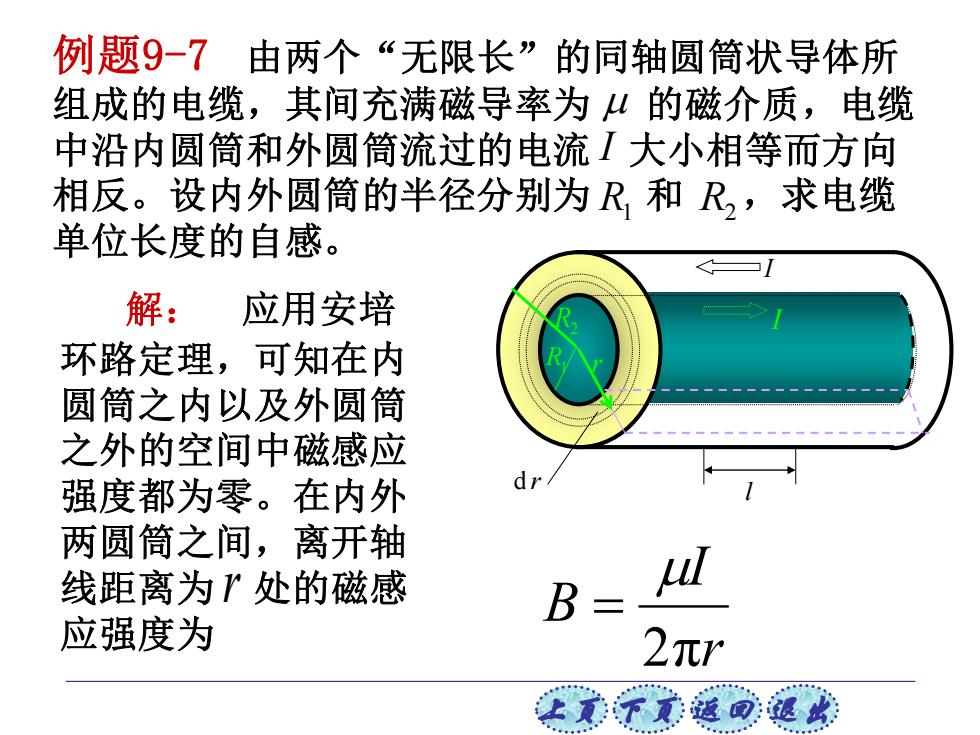
上页 下页 返回 退出 例题9-7 由两个“无限长”的同轴圆筒状导体所 组成的电缆,其间充满磁导率为 的磁介质,电缆 中沿内圆筒和外圆筒流过的电流 大小相等而方向 相反。设内外圆筒的半径分别为 和 ,求电缆 单位长度的自感。 I R1 R2 I I R2 R1 r d r l 解: 应用安培 环路定理,可知在内 圆筒之内以及外圆筒 之外的空间中磁感应 强度都为零。在内外 两圆筒之间,离开轴 线距离为 处的磁感 应强度为 r r I B 2π =