《普通物理学》课程教学资源（PPT课件）第八章 恒定电流的磁场 8-6 磁场对载流导线的作用

§8-6磁场对载流导线的作用 一、安培定律 安培力：载流导线在磁场中受到的磁场力 大小 dF IdlBsin 0 日是电流元与磁感应强度的夹角。 dF方向判断 右手螺旋 安培定律矢量式 dF=Id7 x B 一段任意形状载流导线受到的安培力 F=dF=∫Ial×B 让贰子元道觉退此

上页 下页 返回 退出 §8-6 磁场对载流导线的作用 一、 安培定律 安培力：载流导线在磁场中受到的磁场力 F I l B    d = d  dF = IdlBsin  dF方向判断 右手螺旋   = =  L L F F I l B     d d 一段任意形状载流导线受到的安培力 大小  是电流元与磁感应强度的夹角。 安培定律矢量式

载流导线受到的安培力的微观实质是载流导线中大 量载流子受到洛伦兹力的结果。简单证明如下： 在载流导线上任取一电流元Idl 其中电荷dg沿导线速度为) 电流元长di=dt则dq=ldt 在电流元所在的微小空间区域，磁场可看作匀强的， 按照洛伦兹力公式，可得电流元所受磁场力 dF=dgxB=dr=a×B dt 这就是电流元在磁场中受到的安培力。 让美觉返司退

上页 下页 返回 退出 载流导线受到的安培力的微观实质是载流导线中大 量载流子受到洛伦兹力的结果。简单证明如下： 在载流导线上任取一电流元 I l  d 其中电荷dq沿导线速度为 v  电流元长 dl vdt   = 则 dq = Idt 在电流元所在的微小空间区域，磁场可看作匀强的， 按照洛伦兹力公式，可得电流元所受磁场力 F qv B    d = d  B t l I t   =  d d d I l B   = d  这就是电流元在磁场中受到的安培力

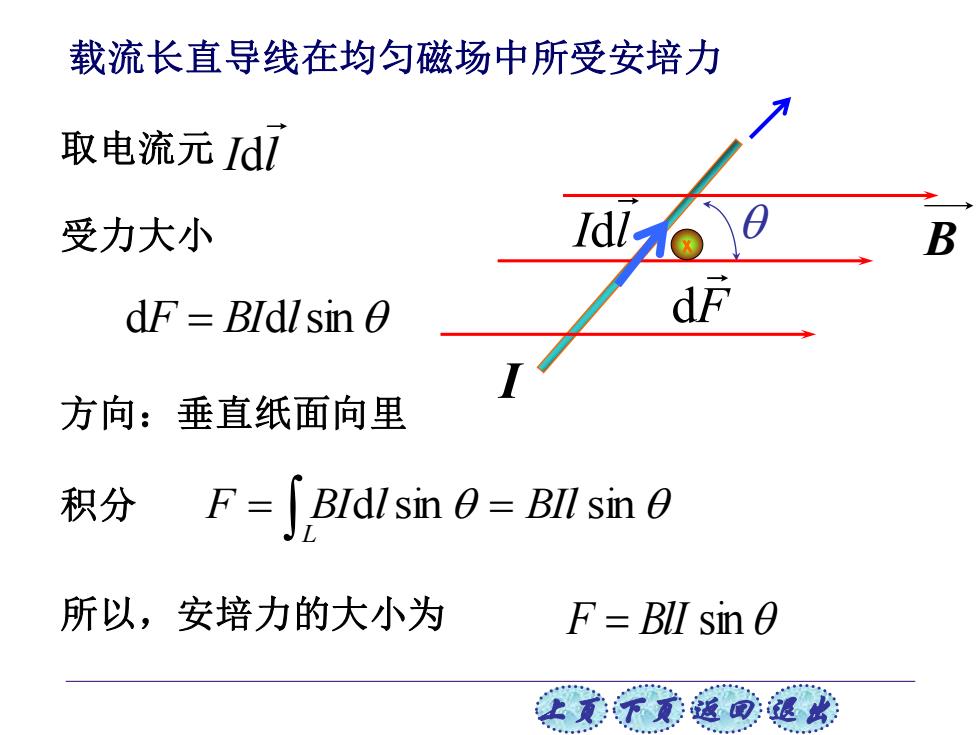
载流长直导线在均匀磁场中所受安培力 取电流元Idl 受力大小 B dF BIdl sin 0 dF 方向：垂直纸面向里 积分F=∫BIdisin=Bll sin 所以，安培力的大小为 F=BlI sin 0

上页 下页 返回 退出 载流长直导线在均匀磁场中所受安培力 dF = BIdlsin  取电流元 I l  d 受力大小 方向：垂直纸面向里 积分  = = L F BIdlsin  BIl sin  F = BlI sin   I B F  d I l  d 所以，安培力的大小为

如果载流导线所处为非均匀磁场，可取电流元，每 段受力d可分解为dF,dF,dF =∫drF=∫dr,F=∫d 然后，求出合力即可。 例题8-6在磁感强度为B 的均匀磁场中，通过一 半径为R的半圆导线中的 电流为1。若导线所在平 面与B垂直，求该导线所 受的安培力。 让美不觉返面：退此

上页 下页 返回 退出 如果载流导线所处为非均匀磁场，可取电流元，每 段受力 F 可分解为  d dF x dF y dF z d F F x x =  d F F y y =  d F F z z =  然后，求出合力即可。 例题8-6 在磁感强度为B 的均匀磁场中，通过一 半径为R的半圆导线中的 电流为I。若导线所在平 面与B垂直，求该导线所 受的安培力。 I

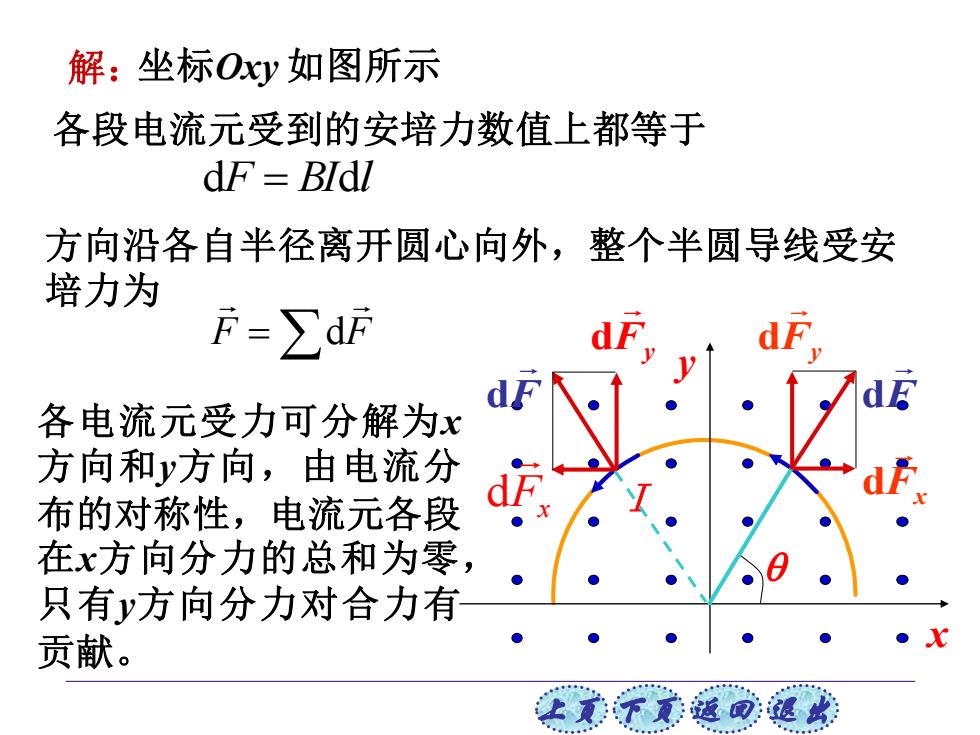
解：坐标Oy如图所示 各段电流元受到的安培力数值上都等于 dF BIdl 方向沿各自半径离开圆心向外，整个半圆导线受安 培力为 F=∑df dF 各电流元受力可分解为x 方向和y方向，由电流分 布的对称性，电流元各段 d方 在x方向分力的总和为零， 只有y方向分力对合力有 贡献

上页 下页 返回 退出 各电流元受力可分解为x 方向和y方向，由电流分 布的对称性，电流元各段 在x方向分力的总和为零， 只有y方向分力对合力有 贡献。 解：坐标Oxy 如图所示 各段电流元受到的安培力数值上都等于 dF = BIdl 方向沿各自半径离开圆心向外，整个半圆导线受安 培力为 F = F   d I x y Fx  d  F  d Fx  d Fy  d F  d Fy  d