
*§10-6二维谐振动的合成 两个同频率的相互垂直的分运动位移表达式 x=A cos(@t+o) y=4 cos(@t+o) 消时间参数,得 七2o=m4 合运动一般是在A向)、24向)范围内的一个 椭圆。 椭圆的性质(方位、长短轴、左右旋)在A1、A2 确定之后,主要决定于△中=20-0。 让式不元通司退
上页 下页 返回 退出 两个同频率的相互垂直的分运动位移表达式 消时间参数,得 合运动一般是在 ( x向)、 ( y向)范围内的一个 椭圆。 1 2A 2A2 *§10-6 二维谐振动的合成 1 10 x A t = + cos( ) 2 20 y A t = + cos( ) 2 2 2 2 2 20 10 20 10 1 2 1 2 2 cos( ) sin ( ) x y x y A A A A + − − = − 椭圆的性质(方位、长短轴、左右旋 )在 A1 、A2 确定之后,主要决定于 = − 20 10

讨论 丈+广-2二co0s4。-o)=sin(6-4) (1)f0f0=0或2m y= A (2)f20f0=元 y= A 让贰下觉返回退
上页 下页 返回 退出 (1) f f 20 10 - = 0 2 或 π x A A y 1 2 = (2) 20 10 f f - = π x A A y 1 2 = − y O x A1 A2 A1 A2 O x y 讨论: 2 2 2 2 2 20 10 20 10 1 2 1 2 2 cos( ) sin ( ) x y x y A A A A + − − = −
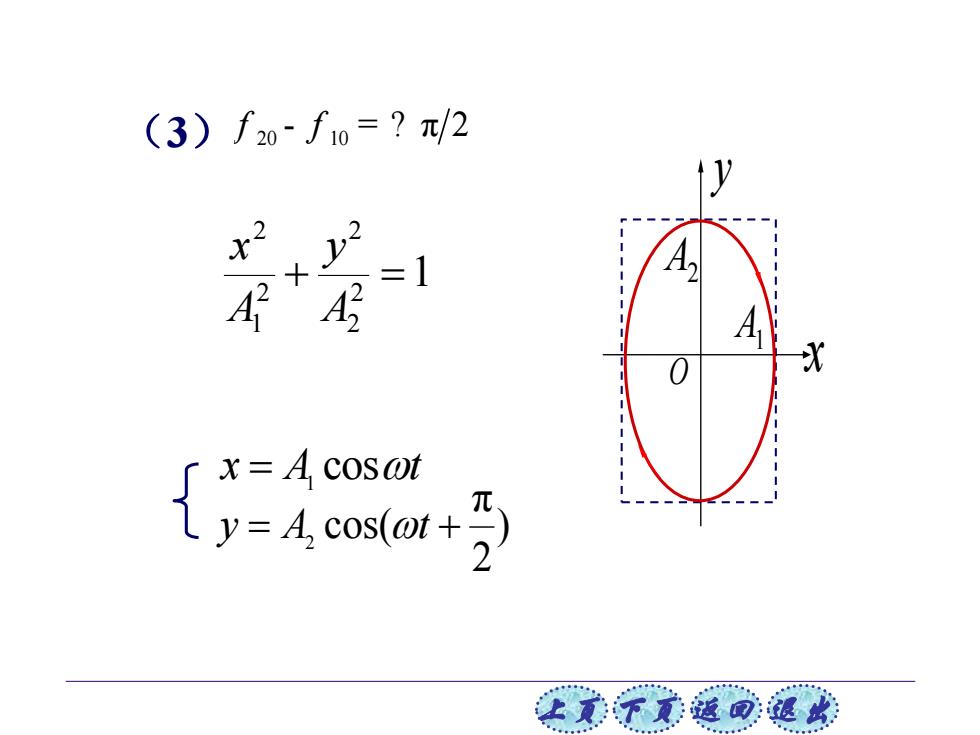
(3)f20f0=?/2 r? =1 X ∫x=Acos0t =.cos+ 让文不美蕴回蕴以
上页 下页 返回 退出 x A cost = 1 ) 2 π cos( y = A2 t + (3) 20 10 f f - = ? π 2 1 2 2 2 2 1 2 + = A y A x A1 A2 O x y
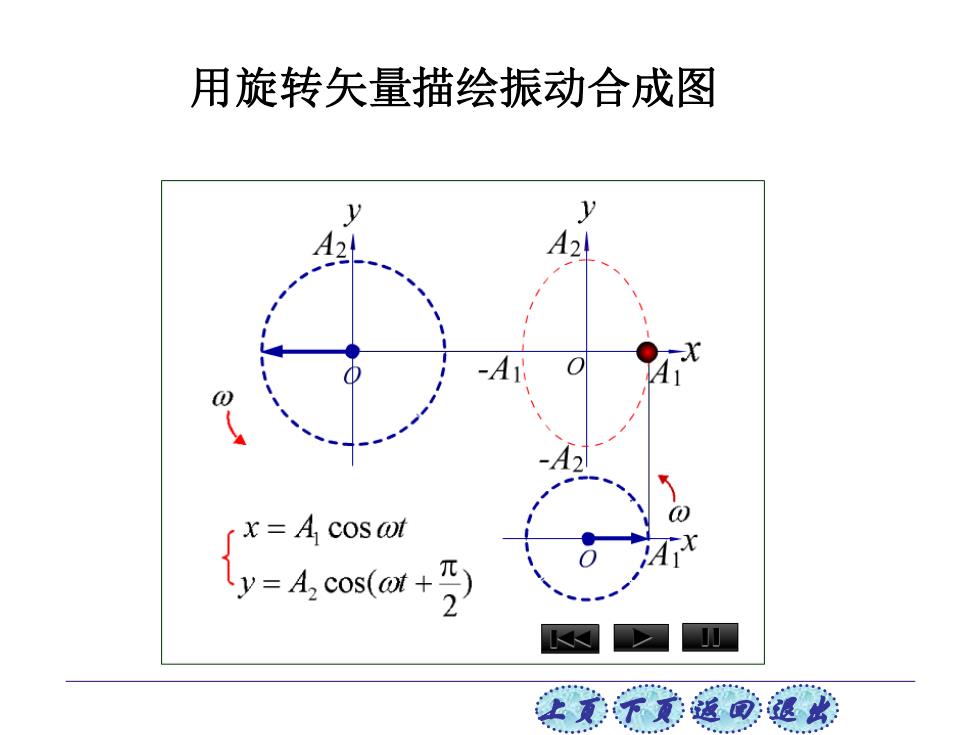
用旋转矢量描绘振动合成图 y 4? [4 coso y=A,cos(at+ 女意不贰通可退此
上页 下页 返回 退出 用旋转矢量描绘振动合成图
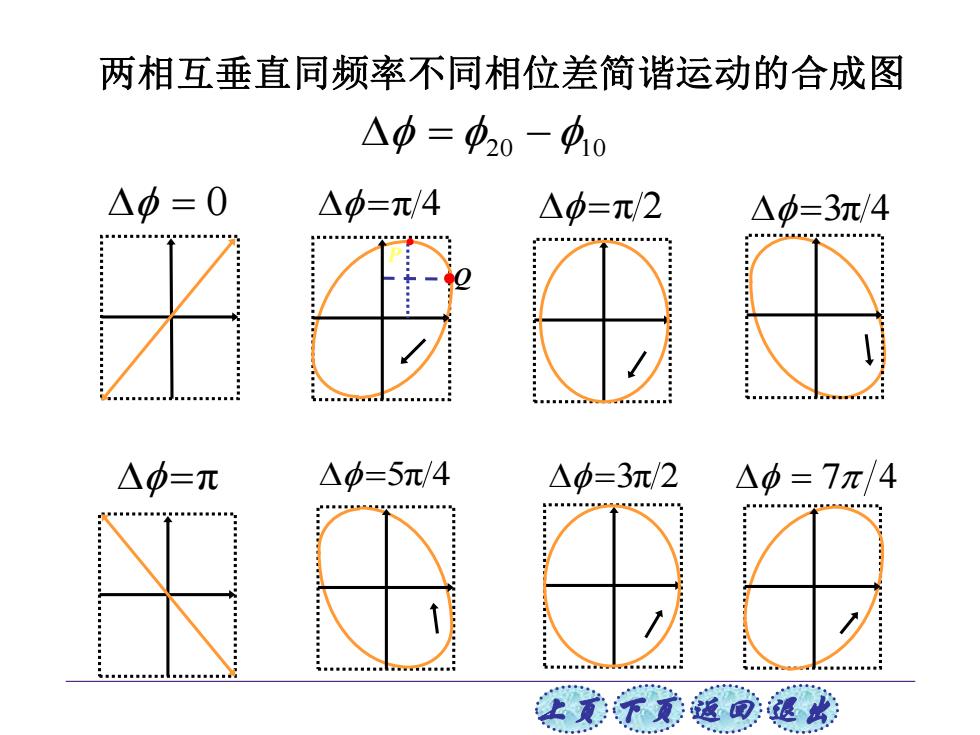
两相互垂直同频率不同相位差简谐运动的合成图 △0=中20-40 △中=0 △中=π/4 △中=π/2 △b=3π/4 ■■ △中=π △中=5π/4 △0=3π/2 △中=7π/4 让美下元返回:退欢
上页 下页 返回 退出 Q P . = π 4 · = 20 −10 = 0 = π 2 = 3π 4 = π 两相互垂直同频率不同相位差简谐运动的合成图 = 5π 4 = 3π 2 = 7 4