
电路A教案 第二章电阻电路的等效变换 小。因此并连电阻电路可作分流电路。 4.功率 各电阻的功率为: =GR=G,.,里=G4,.,卫.=G 所以: R:P::B:.P=G:G::G::G 总功率: P=Gw2=(G+G+.+G+.+G)2 =G42+G2+.+G2+.+G,2=++.+P 结论:电阻并联时,各电阻消耗的功率与电阻大小成反比,即电阻值大者消耗的 功率小:等效电阻消耗的功率等于各并连电阻消耗功率的总和。 三、电阻的串、并联 电路中有电阻的串联,又有电阻的并联的电路称电阻的串并联电路。电阻相串联 的部分具有电阻串联电路的特点,电阻相并联的部分具有电阻并联电路的特点。 1.求解串、并联电路的一般步骤: (1)求出等效电阻或等效电导: (2)应用欧姆定律求出总电压或总电流: (3)应用欧姆定律或分压、分流公式求各电阻上的电流和电压。 因此,分析串并联电路的关键问题是判别电路的串、并联关系。 2。判别电路的串并联关系一般应掌握下述4点: (1)看电路的结构特点。若两电阻是首尾相联就是串联,是首首尾尾相联就是 并联。 (2)看电压电流关系。若流经两电阻的电流是同一个电流,那就是串联若两 电组上承受的是同一个电压,那就是并联。 (3)在不改变电路连接的情况下,电阻的位置可以随便移动。对电路中的短线 路可以任意压缩与伸长;对多点接地可以用短路线相连。一般,如果真正是电阻串联 电路的问题,都可以判别出来。 (4)找出等电位点。对于具有对称特点的电路,若能判断某两点是等电位点, 则根据电路等效的概念,一是可以用短接线把等电位点联起来:二是把联接等电位点 的支路断开(因支路中无电流),从而得到电阻的串并联关系。 第6页共18页
电路 A 教案 第二章 电阻电路的等效变换 第 6 页 共 18 页 小。因此并连电阻电路可作分流电路。 4. 功率 各电阻的功率为: 所以: 总功率: 结论:电阻并联时,各电阻消耗的功率与电阻大小成反比,即电阻值大者消耗的 功率小;等效电阻消耗的功率等于各并连电阻消耗功率的总和。 三、电阻的串、并联 电路中有电阻的串联,又有电阻的并联的电路称电阻的串并联电路。电阻相串联 的部分具有电阻串联电路的特点,电阻相并联的部分具有电阻并联电路的特点。 1. 求解串、并联电路的一般步骤: (1)求出等效电阻或等效电导; (2)应用欧姆定律求出总电压或总电流; (3)应用欧姆定律或分压、分流公式求各电阻上的电流和电压。 因此,分析串并联电路的关键问题是判别电路的串、并联关系。 2. 判别电路的串并联关系一般应掌握下述 4 点: (1)看电路的结构特点。若两电阻是首尾相联就是串联,是首首尾尾相联就是 并联。 (2)看电压电流关系。若流经两电阻的电流是同一个电流,那就是串联;若两 电组上承受的是同一个电压,那就是并联。 (3)在不改变电路连接的情况下,电阻的位置可以随便移动。对电路中的短线 路可以任意压缩与伸长;对多点接地可以用短路线相连。一般,如果真正是电阻串联 电路的问题,都可以判别出来。 (4)找出等电位点。对于具有对称特点的电路,若能判断某两点是等电位点, 则根据电路等效的概念,一是可以用短接线把等电位点联起来;二是把联接等电位点 的支路断开(因支路中无电流),从而得到电阻的串并联关系
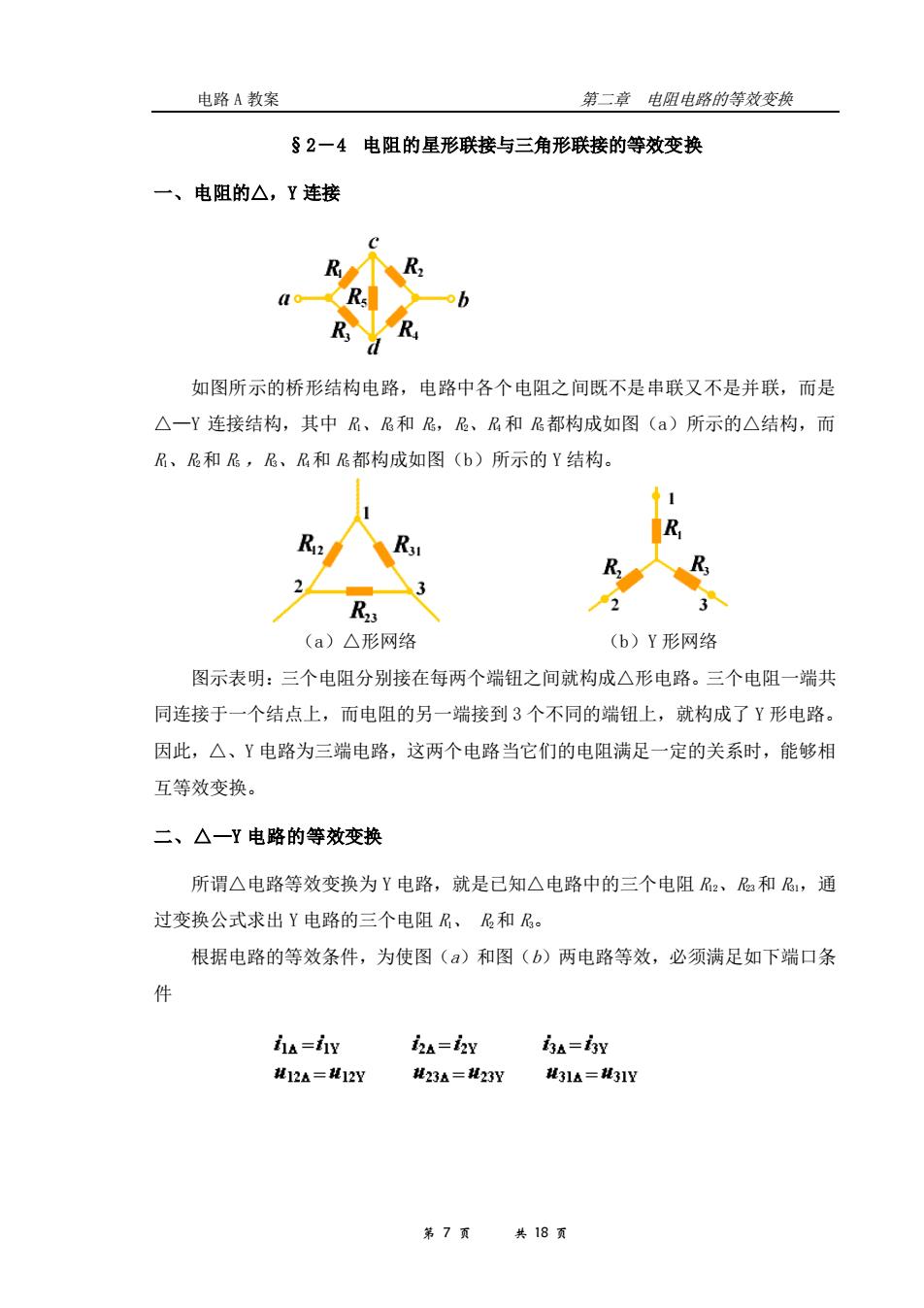
电路A教案 第二章电阻电路的等效变换 §2一4电阻的星形联接与三角形联接的等效变换 一、电阻的△,Y连接 R ao -b R 如图所示的桥形结构电路,电路中各个电阻之间既不是串联又不是并联,而是 △一Y连接结构,其中R、尼和尼,尼、R和尼都构成如图(a)所示的△结构,而 R、尼和尼,尼、R和都构成如图(b)所示的Y结构。 1 R R 3 R 2 3 (a)△形网络 (b)Y形网络 图示表明:三个电阻分别接在每两个端钮之间就构成△形电路。三个电阻一端共 同连接于一个结点上,而电阻的另一端接到3个不同的端钮上,就构成了Y形电路, 因此,△、Y电路为三端电路,这两个电路当它们的电阻满足一定的关系时,能够相 互等效变换。 二、△一Y电路的等效变换 所谓△电路等效变换为Y电路,就是已知△电路中的三个电阻R2、尼和尼,通 过变换公式求出Y电路的三个电阻R、尼和尼。 根据电路的等效条件,为使图(a)和图(b)两电路等效,必须满足如下端口条 件 ha=hy ia=iy B=y 12a=12Y23a=23Y 31a=31Y 第7页 共18页
电路 A 教案 第二章 电阻电路的等效变换 第 7 页 共 18 页 §2-4 电阻的星形联接与三角形联接的等效变换 一、电阻的△,Y 连接 如图所示的桥形结构电路,电路中各个电阻之间既不是串联又不是并联,而是 △—Y 连接结构,其中 R1、R3和 R5,R2、R4 和 R5都构成如图(a)所示的△结构,而 R1、R2和 R5 ,R3、R4和 R5都构成如图(b)所示的 Y 结构。 (a)△形网络 (b)Y 形网络 图示表明:三个电阻分别接在每两个端钮之间就构成△形电路。三个电阻一端共 同连接于一个结点上,而电阻的另一端接到 3 个不同的端钮上,就构成了 Y 形电路。 因此,△、Y 电路为三端电路,这两个电路当它们的电阻满足一定的关系时,能够相 互等效变换。 二、△—Y 电路的等效变换 所谓△电路等效变换为 Y 电路,就是已知△电路中的三个电阻 R12、R23和 R31,通 过变换公式求出 Y 电路的三个电阻 R1、 R2和 R3。 根据电路的等效条件,为使图(a)和图(b)两电路等效,必须满足如下端口条 件