第一章电路的基本概念和基本定律 习题解答 1-1题1-1图所示电路,求各段电路的电压U如及各元件的功率,并说明元件是消耗 功率还是对外提供功率? a024口 -ob -8V -10V (a) (6) (c) ob ao ①1Aoba0 -8V -6V 16V (d) (e) (f) 题1-1图 解根据功率计算公式及题给条件,得 (a)Uab=6V,P=6×2=12W 消耗功率 (b)Uab=-8V,P=1×(-8)=-8W 提供功率 (c)Ua=-10V,P=-(-8)×(-10)F-80W 提供功率 (d)Uab=-8V,P=-(-2)×(-8=-16W 提供功率 (e)Ua=-(-6=6V,P=-(-1)×(-6=-6W 提供功率 (f)Uab=-16V,P=(-2)×16=-32W 提供功率 1-2在题1-2图所示各元件中,已知:元件A吸收66W功率,元件B发出25W功 率;元件C吸收负68W功率,求iA、B和iC。 。回4 6V B -4V 题1-2图 解根据题意,对元件A,有 P-6i=6,-6=A 6 对元件B,有 PM=5e-25,4g-25-5V -5 对元件C,有 P-4=-68,k=-68=17A -4 -1-
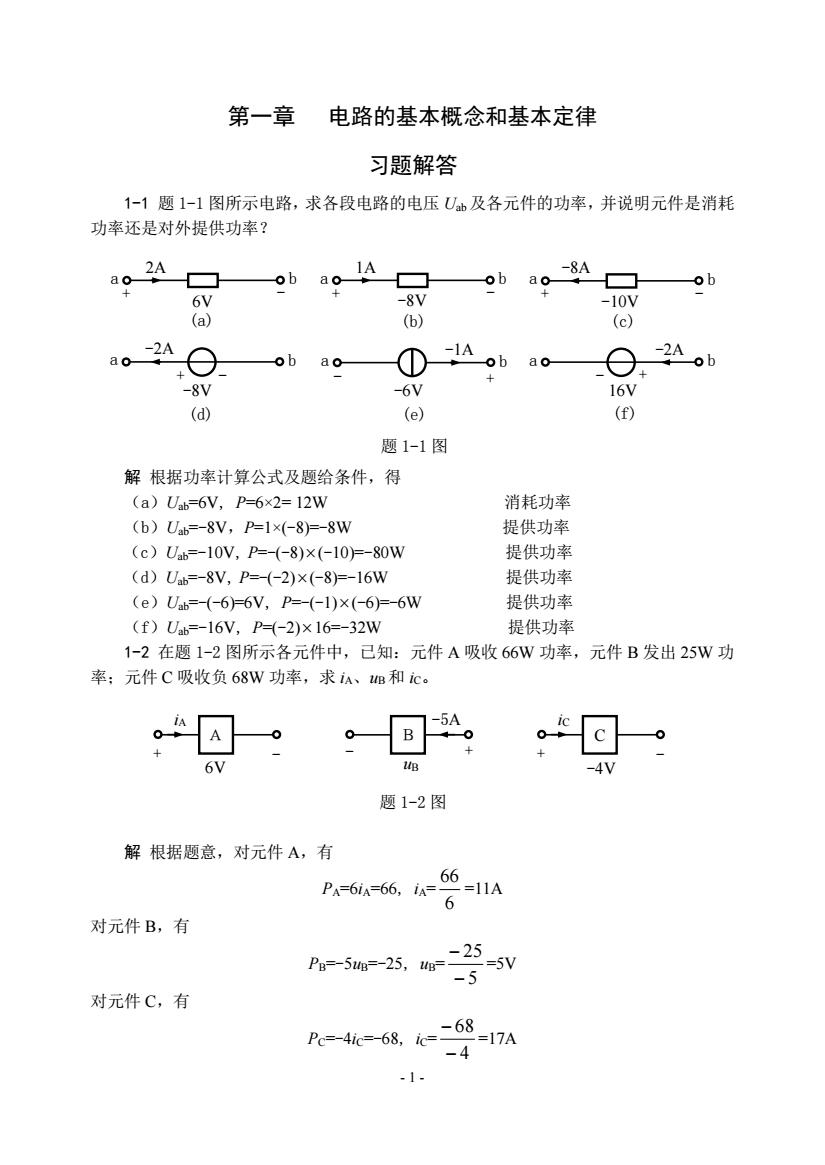
- 1 - 第一章 电路的基本概念和基本定律 习题解答 1-1 题 1-1 图所示电路,求各段电路的电压 Uab及各元件的功率,并说明元件是消耗 功率还是对外提供功率? 解 根据功率计算公式及题给条件,得 (a)Uab=6V, P=6×2= 12W 消耗功率 (b)Uab=-8V,P=1×(-8)=-8W 提供功率 (c)Uab=-10V, P=-(-8) (-10)=-80W 提供功率 (d)Uab=-8V, P=-(-2) (-8)=-16W 提供功率 (e)Uab=-(-6)=6V, P=-(-1) (-6)=-6W 提供功率 (f)Uab=-16V, P=(-2) 16=-32W 提供功率 1-2 在题 1-2 图所示各元件中,已知:元件 A 吸收 66W 功率,元件 B 发出 25W 功 率;元件 C 吸收负 68W 功率,求 iA、uB和 iC。 解 根据题意,对元件 A,有 PA=6iA=66, iA= 6 66 =11A 对元件 B,有 PB=-5uB=-25, uB= 5 25 =5V 对元件 C,有 PC=-4iC=-68, iC= 4 68 =17A (a) (b) (d) (e) (f) a 6V + - b 2A a -8V + - b 1A a -10V + - b -8A (c) a -8V + - b -2A a 16V - + b -2A a -6V - + b -1A 题 1-1 图 题 1-2 图 6V + - iA A uB - + B -5A -4V + - iC C

1-3题1-3图所示电路中,5个元件代表电源或负载。通过实验测量得知:仁-2A 12=3A,I3=5A,U1=70V,U2=-45V,U=30V,U=-40V,Us=-15V. (1)试指出各电流的实际方向和各电压的实际极性? (2)判断那些元件是电源:那些元件是负载? (3)计算各元件的功率,验证功率平衡? U. 56 3 U 2 + 题1-3图 解(1)图中虚线箭头为各支路电流的实际方向。⊕、日极性为各元件电压的实际 极性 (2)按实际方向判断元件的状态:U、I关联者为负载,U、I非关联者为电源。据此 可判断元件1、2为电源,元件3、4为负载。也可按书上的方法判断如下: P,=UU11=70×(-2)=-140W P2=U2=45×3=-135W P3=UU=30×5=150W P4=U4l1=-40x(-2)=80W P=-LU=-(-15)×3=45W 因为P1<0、P2<0,故元件1、2为电源:P>0、P>0、P>0,故元件3、4、5为负载。 (3)各元件的功率见(2),据此有 P+P2+P3+P4+Ps=-140-135+150+80+45=0 可知功率平衡, 1-4求题1-4图所示电路中各元件的功率,并验证功率平衡。 R 题1-4图 解由欧姆定律及KCL,得 .2
- 2 - 1-3 题 1-3 图所示电路中,5 个元件代表电源或负载。通过实验测量得知:I1=-2A, I 2=3A,I 3=5A,U1=70V,U2=-45V,U3=30V,U4=-40V,U 5=-15V。 (1)试指出各电流的实际方向和各电压的实际极性? (2)判断那些元件是电源;那些元件是负载? (3)计算各元件的功率,验证功率平衡? 解(1)图中虚线箭头为各支路电流的实际方向。 、 极性为各元件电压的实际 极性。 (2)按实际方向判断元件的状态:U、I 关联者为负载,U、I 非关联者为电源。据此 可判断元件 1、2 为电源,元件 3、4 为负载。也可按书上的方法判断如下: P1=U1I1=70×(-2)=-140 W P2=U2I2=-45× 3=-135 W P3=U3I3=30× 5=150 W P4=U4I1=-40×(-2)=80 W P5=-U5I2=-(-15)×3=45 W 因为 P1<0、P2<0,故元件 1、2 为电源;P3>0、P4>0、P5>0,故元件 3、4、5为负载。 (3) 各元件的功率见(2),据此有 P1+P2+P3+P4+P5=-140-135+150+80+45=0 可知功率平衡。 1-4 求题 1-4 图所示电路中各元件的功率,并验证功率平衡。 解 由欧姆定律及 KCL,得 题 1-3 图 + - + - - - + + + + + + + + - - - - - - U4 U5 U1 1 U3 U2 4 5 3 2 3 I 2 I 1 I R1 R1 I I 5 2A 10V 2 + - R2 US 题 1-4 图
I=I8-2=5-2=3A 各元件的功率为 P=-10I=-10×3=-30w P=-1s(1sR2+Us)=-2(2×5+10)=-40W P%=IRR=52×2=50w P%=1R2=22×5=20w Ps+Ps+P。+P=-30-40+50+20=0 可知功率平衡。 1-5题1-5图所示电路,写出各元件u与i的约束方程。 1/20uF h (a) (6) (c) 。①24。 (d) (e) (f) 题1-5图 解根据各元件的伏安关系及题给条件得 (a)e-2.5×10i (b)e-30x10=-3×10d (c)F-20x10d恤=-2x10 (d)u-6V dr (e)i=2A (f)1F-6V 1-6将额定电压为6、额定功率为P的电热丝(可看作线性电阻)切成长,然后 3 加上电压U,问此时电热丝消耗的功率P为多少? 解由题意可知,电热丝的原电阻为 -3
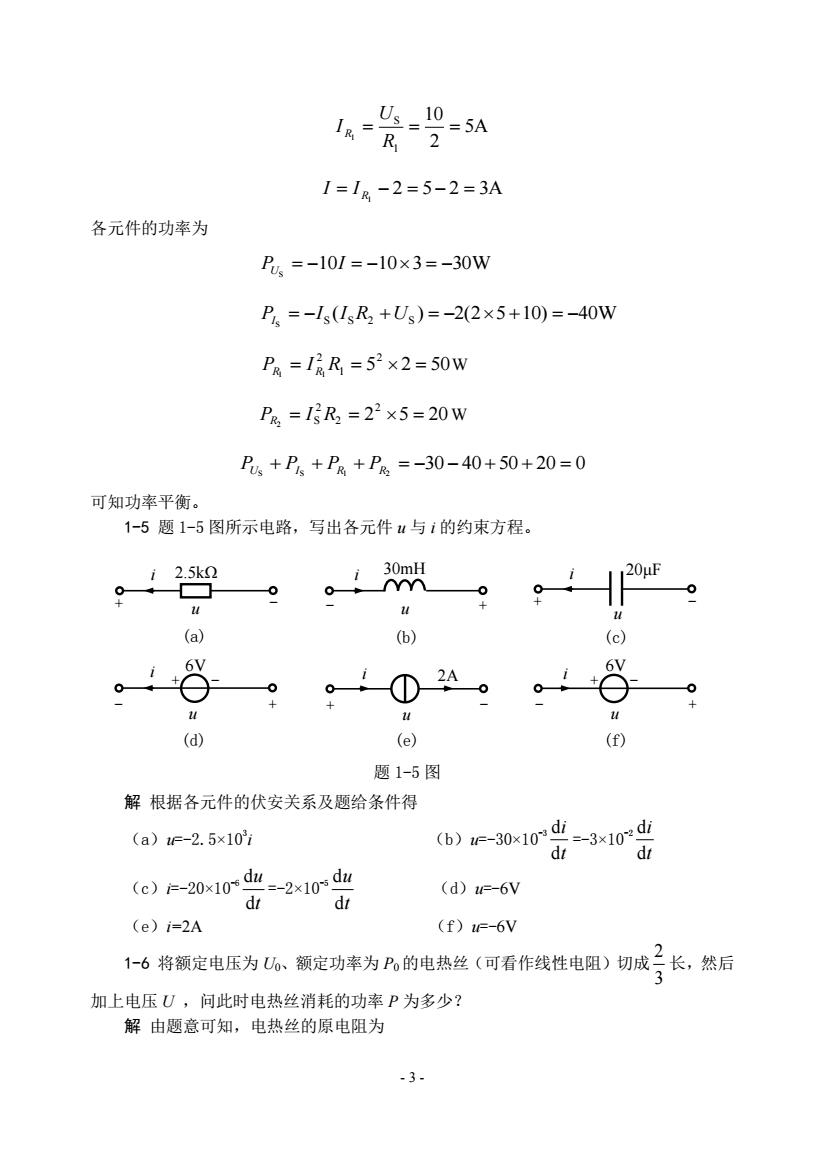
- 3 - 5A 2 10 1 S 1 R U I R 2 5 2 3A 1 I I R 各元件的功率为 PUS 10I 103 30W PIS I S (I SR2 US ) 2(25 10) 40W 5 2 50 2 1 2 1 1 PR I R R W 2 5 20 2 2 2 PR2 I S R W 30 40 50 20 0 S S 1 2 PU PI PR PR 可知功率平衡。 1-5 题 1-5 图所示电路,写出各元件 u 与 i 的约束方程。 解 根据各元件的伏安关系及题给条件得 (a)u=-2.5×103 i (b)u=-30×10-3 t i d d =-3×10-2 t i d d (c)i=-20×10-6 t u d d =-2×10-5 t u d d (d)u=-6V (e)i=2A (f)u=-6V 1-6 将额定电压为 U0、额定功率为 P0 的电热丝(可看作线性电阻)切成 3 2 长,然后 加上电压 U ,问此时电热丝消耗的功率 P 为多少? 解 由题意可知,电热丝的原电阻为 (a) (b) (d) (e) (f) u (c) 6V + - i 6V + - - + 2A 题 1-5 图 + - i 2.5kΩ - u + i 30mH + - i 20μF u u - + i u + - u i
切成子长时的电阻为 此时电热丝消耗的功率为 v v3v3Upo P= 飘园 P 1-7题1-7图(a)电容中电流i的波形如图(b)所示,已知(0)=1V,试求=1s、 =3s和=5s时电容电压u。 (a) (6) 题1-7图 解由图(b)所示电流i的波形图,可求得 2.51 {)}A=了-2.5r10 2s≤K4s (-5 24s 0.6252+1 02s {u(t)w={0.625+51-4 2s≤K4s -2.5+16 24s 当=15,=3s和5s时,有 1=0.625×12+1=1.625V -4
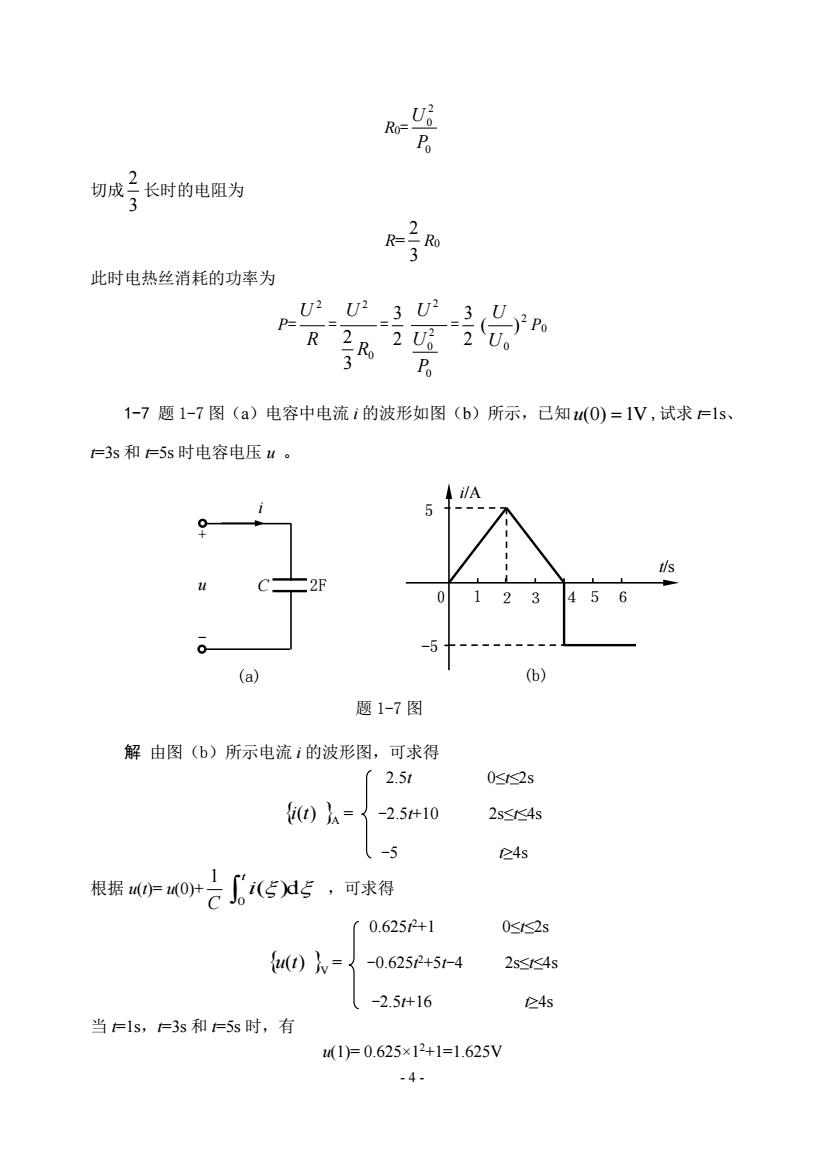
- 4 - R0= 0 2 0 P U 切成 3 2 长时的电阻为 R= 3 2 R0 此时电热丝消耗的功率为 P= R U 2 = 0 2 3 2 R U = 2 3 0 2 0 2 P U U = 2 3 2 0 ( ) U U P0 1-7 题 1-7 图(a)电容中电流 i 的波形如图(b)所示,已知 u(0) 1V ,试求 t=1s、 t=3s 和 t=5s 时电容电压 u 。 解 由图(b)所示电流 i 的波形图,可求得 2.5t 0≤t≤2s A i(t) = -2.5t+10 2s≤t≤4s -5 t≥4s 根据 u(t)= u(0)+ C 1 ( )d 0 t i ,可求得 0.625t 2+1 0≤t≤2s V u(t) = -0.625t 2+5t-4 2s≤t≤4s -2.5t+16 t≥4s 当 t=1s,t=3s 和 t=5s 时,有 u(1)= 0.625×12+1=1.625V 题 1-7 图 (b) i/A t/s 5 -5 0 1 2 3 4 5 6 (a) i u + - C 2F
3=-0.625×32+5×3-4=5.375V 5=-25×5+16=35V 1-8题1-8图(a)中,电感电压的波形如图(b)所示,己知i(0)=2A,试求当=1s、 仁2s、=3s和=5s时电感电流1. 10 t/s L .5H 0 -10 (6) 题1-8图 解由图()所示“的波形图,可得 /51 0s<2s -10+30 {)w={0 3s≤K4s 10r-50 4s≤5s 0 25s 根据(00:2(55,可求出 「2+2 0<K<2s -2r2+12-10 2s≤13s )A= 3s≤14s 22-20+56 4sst<5s 6 25s 当=1s、=2s、=3s和=5s时,有 iI)=12+2=3A i(2y-2×22+12×2-10=6A i(3F-2×32+12×3-10=8A i5)2×52-20x5+56-6A 1-9图()所示电路中,求两电源的功率,并指出那个元件吸收功率?那个元件发 出功率?图(b)所示电路中,指出哪个元件可能吸收或发出功率? 解(a)由题给条件及功率计算公式得 -5-
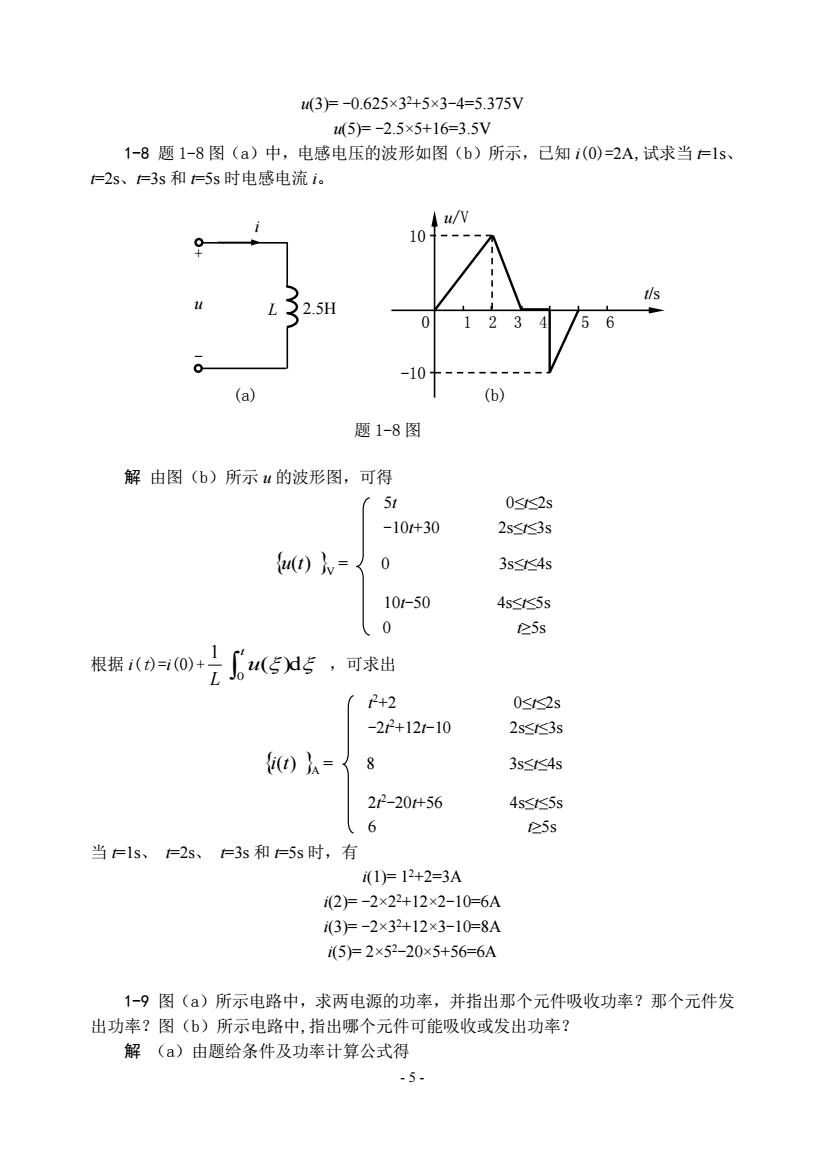
- 5 - u(3)= -0.625×32+5×3-4=5.375V u(5)= -2.5×5+16=3.5V 1-8 题 1-8 图(a)中,电感电压的波形如图(b)所示,已知 i(0)=2A,试求当 t=1s、 t=2s、t=3s 和 t=5s 时电感电流 i。 解 由图(b)所示 u 的波形图,可得 5t 0≤t≤2s -10t+30 2s≤t≤3s V u(t) = 0 3s≤t≤4s 10t-50 4s≤t≤5s 0 t≥5s 根据 i(t)=i(0)+ L 1 ()d 0 t u ,可求出 t 2+2 0≤t≤2s -2t 2+12t-10 2s≤t≤3s A i(t) = 8 3s≤t≤4s 2t 2-20t+56 4s≤t≤5s 6 t≥5s 当 t=1s、 t=2s、 t=3s 和 t=5s 时,有 i(1)= 12+2=3A i(2)= -2×22+12×2-10=6A i(3)= -2×32+12×3-10=8A i(5)= 2×52-20×5+56=6A 1-9 图(a)所示电路中,求两电源的功率,并指出那个元件吸收功率?那个元件发 出功率?图(b)所示电路中,指出哪个元件可能吸收或发出功率? 解 (a)由题给条件及功率计算公式得 -10 10 u/V t/s 0 1 2 3 4 5 6 (b) 题 1-8 图 (a) i u + - L 2.5H