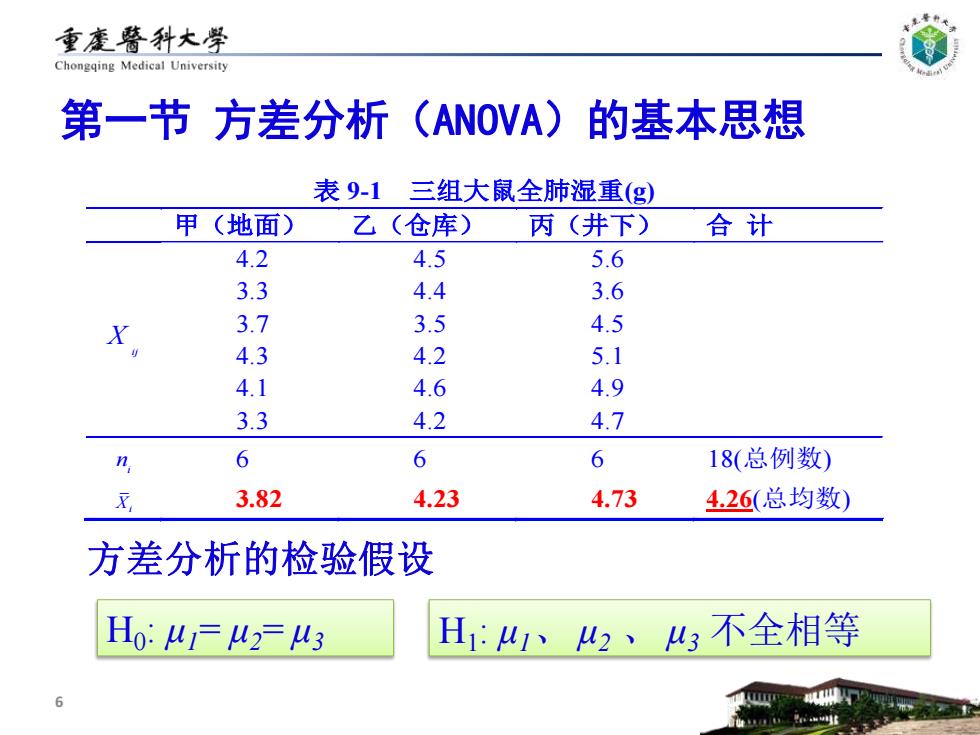
重废警科大学 Chongqing Medical University 第一节方差分析(ANOVA)! 的基本思想 表9-1三组大鼠全肺湿重(g) 甲(地面) 乙(仓库) 丙(井下) 合计 4.2 4.5 5.6 3.3 4.4 3.6 X 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 n 6 6 6 18(总例数) 3.82 4.23 4.73 4.26(总均数) 方差分析的检验假设 H0:4F23 H1:、42、43不全相等
表 9-1 三组大鼠全肺湿重(g) 甲(地面) 乙(仓库) 丙(井下) 合 计 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 i j X 3.3 4.2 4.7 i n 6 6 6 18(总例数) Xi 3.82 4.23 4.73 4.26(总均数) 6 H0 : μ1= μ2= μ3 H1 : μ1、 μ2 、 μ3 不全相等 方差分析的检验假设 第一节 方差分析(ANOVA)的基本思想
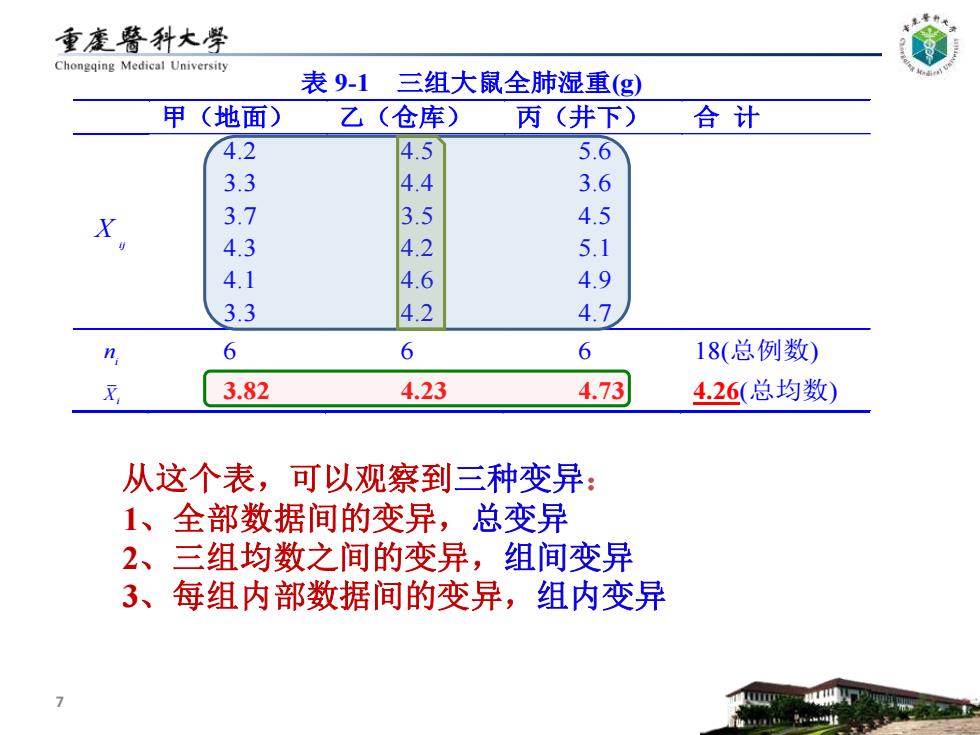
重废警科大学 Chongqing Medical University 表9-1 三组大鼠全肺湿重(g) 甲(地面) 乙(仓库) 丙(井下) 合计 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4:6 4.9 3.3 4.2 4.7 6 6 6 18(总例数) 3.82 4.23 4.73 4.26(总均数) 从这个表,可以观察到三种变异: 1、全部数据间的变异,总变异 2、三组均数之间的变异,组间变异 3、每组内部数据间的变异,组内变异
表 9-1 三组大鼠全肺湿重(g) 甲(地面) 乙(仓库) 丙(井下) 合 计 i j X 4.2 4.5 5.6 3.3 4.4 3.6 3.7 3.5 4.5 4.3 4.2 5.1 4.1 4.6 4.9 3.3 4.2 4.7 i n 6 6 6 18(总例数) Xi 3.82 4.23 4.73 4.26(总均数) 7 从这个表,可以观察到三种变异: 1、全部数据间的变异,总变异 2、三组均数之间的变异,组间变异 3、每组内部数据间的变异,组内变异

重廣警科大学 Chongqing Medical University 变异(离均差平方和)的分解 1、 总变异(SS总,total variation) 全部测量值大小各异,与总均值之间的 差异称为总变异,即X,与灭之间的差异。 SSa=∑∑(X,-X)1 i=1j=1 本例,SS总=6.5628 8
变异(离均差平方和)的分解 1、总变异(SS总,total variation) 全部测量值大小各异,与总均值之间的 差异称为总变异,即Xij 与 之间的差异。 = = = − k i n j i j i SS X X 1 1 2 总 ( ) X 8 本例,SS总=6.5628

重废警科大学 Chongqing Medical University 2、组间变异 2(SS组间,variation between groups) ·三种环境下全肺湿重的平均值各不相同,这种 变异称为组间变异 ” 是组内均值X,与总均值X之差的平方和 SS同=∑∑(X,-X)2=∑n(仅,-) i=l 组间变异SS组▣反映: >三种不同环境对全肺湿重的影响(处理的效应) >同时也包括随机因素的影响(随机误差) 本例,SS组间=2.5278
2、组间变异(SS组间,variation between groups) • 三种环境下全肺湿重的平均值各不相同,这种 变异称为组间变异 • 是组内均值 与总均值 之差的平方和 2 1 1 2 SS (X X ) n (X X ) i k i i k i n j i i = − = − = = 组间 组间变异SS组间反映: ➢三种不同环境对全肺湿重的影响(处理的效应) ➢同时也包括随机因素的影响(随机误差) Xi X 9 本例,SS组间=2.5278

重废警科大学 Chongqing Medical University 3、组内变异(SS组内,variation within groups) ·在相同环境下生活,全肺湿生也各不相同,这种变 异称为组内变异 ·组内各个观测值X,与本组内均值x,之间差的平方和 SS内=∑∑(X,-X,)月 i=l i 组内变异SS组内反映: 本例, >随机因素的影响(随机误差) SS组内=4.0350 故,组内变异也常记为SS误差 10
3、组内变异(SS组内,variation within groups) • 在相同环境下生活,全肺湿生也各不相同,这种变 异称为组内变异 • 组内各个观测值 与本组内均值 之间差的平方和 2 1 1 ( ) i k i n j SS Xi j X i = − = = 组内 Xij Xi 10 组内变异SS组内反映: ➢随机因素的影响(随机误差) 故,组内变异也常记为SS误差 本例, SS组内=4.0350