
重废警科大学 Chongqing Medical University 常用概率分布 卫生统计学教研室 田考聪
常用概率分布 卫生统计学教研室 田考聪

重废警科大学 Chongqing Medical University 常用概率分布 二项分布 1.二项分布的概念 例换窘额缓个珠从中姿整男 解:由于是有只抽样,故每公摸到黄球的撼率均为QA,摸到归球的趣 率为0.。设摸到黄球的闪数为X,若次摸球中命X次摸到黄球,后书 次摸到白球,则相应的概率为: 0.40.65-x 由于摸到黄球可能发生在5次摸球的任意X次中,故5 次摸球中有X次摸到黄球的概率为: C0.40.65-x
常用概率分布 一、二项分布 1.二项分布的概念 例:一袋中装有2黄、3白共5个乒乓球。从中每次摸出1个,然后放回再 摸 先后摸5次,问摸到0、1、2、3、4、5次黄球的概率各有多大? 解:由于是有放回抽样,故每次摸到黄球的概率均为0.4,摸到白球的概 率为0.6。设摸到黄球的次数为X,若5次摸球中前X次摸到黄球,后5- X次摸到白球,则相应的概率为: X 5−X 0.4 0.6 由于摸到黄球可能发生在5次摸球的任意X次中,故5 次摸球中有X次摸到黄球的概率为: X X X C 5− 5 0.4 0.6

重廣警科大学 Chongqing Medical University 本例的实验有以下三个特点: 每次摸球是彼此独立的: 。 每次摸球只有两种可能的结果; ·每次摸球出现某种结果的概率不变。 满足上述三个条件的随机试验称为Bernoullit试验。本例 摸了5次球,即进行了5次Bernoulli试验。 一般地,在n次Bernoulli试验中,事件A出现的概率为π 设为事件4出现的次数,则是一个离散型随机变量, 它服从二项分布,记为Bn,d,其概率函数为: P(x)=P(X=x)=Cπ*(1-π)”-xx=0,1,2,3,.,n n! C= 式(5-1) xl(n-x)!
本例的实验有以下三个特点: • 每次摸球是彼此独立的; • 每次摸球只有两种可能的结果; • 每次摸球出现某种结果的概率不变。 满足上述三个条件的随机试验称为Bernoulli试验。本例 摸了5次球,即进行了5次Bernoulli试验。 一般地,在n次Bernoulli试验中,事件A出现的概率为π ,设x为事件A出现的次数,则x是一个离散型随机变量, 它服从二项分布,记为B(n,π),其概率函数为: ( ) ( ) (1 ) 0,1,2,3, , ! !( )! x x n x n x n P x P X x C x n n C x n x − = = = − = = − 式(5-1)

重废警科大学 Chongqing Medical University 在n次Bernoullit试验中, 事件A至多出现k次的概率为 2P)=2Cx1-π) x=0 事件A至少出现k次的概率为 ∑Px)=1-∑Cπ'1-) =0 例1:临床上用针灸治疗某型头痛,有效的概率为0.6, 现以该法治疗3例,其中2例有效的概率是多少? 治疗结果为有效和无效两类,每个患者是否有效不 受其他病例的影响,有效概率均为0.6,符合二项分布条 件。本例π=0.6,=3,随机治疗3例,有效例数为2的概 率为: C0.62(1-0.6)3-2=0.432
在n次Bernoulli试验中, 事件A至多出现k次的概率为 事件A至少出现k次的概率为 0 0 ( ) (1 ) k k x x n x n x x P x C − = = = − 1 0 ( ) 1 (1 ) n k x x n x n x k x P x C − − = = = − − 例1:临床上用针灸治疗某型头痛,有效的概率为0.6, 现以该法治疗3例,其中2例有效的概率是多少? 治疗结果为有效和无效两类,每个患者是否有效不 受其他病例的影响,有效概率均为0.6,符合二项分布条 件。本例π= 0.6,n =3,随机治疗3例,有效例数为2的概 率为: 0.6 (1 0.6) 0.432 2 2 3 2 3 − = − C
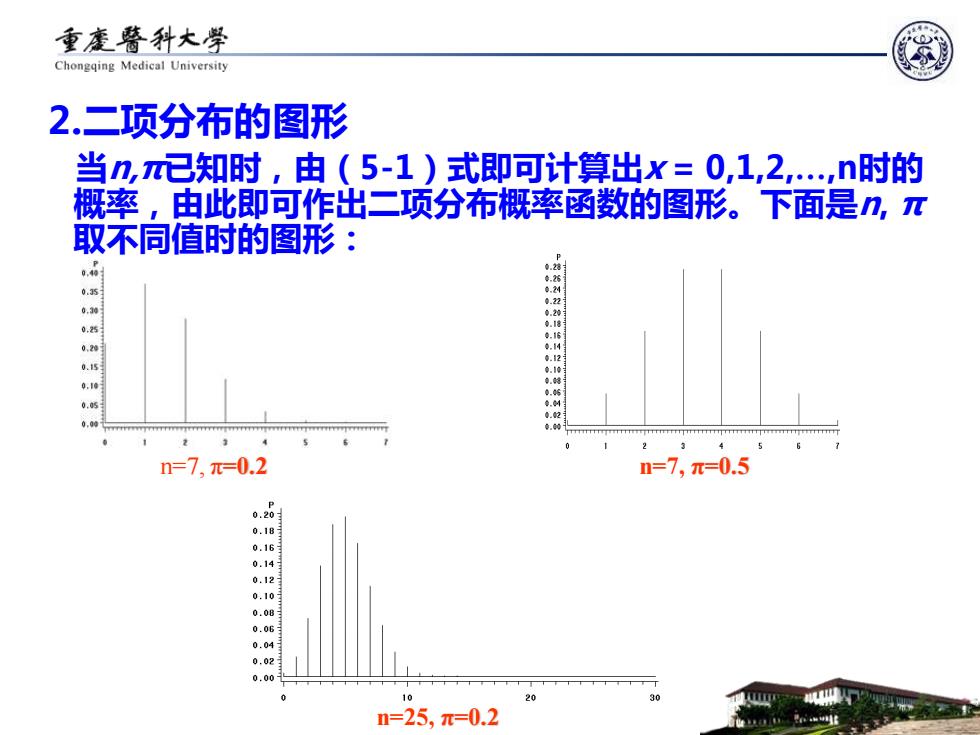
重废警科大学 Chongqing Medical University 2.二项分布的图形 当n,己知时,由(5-1)式即可计算出x=0,1,2,n时的 概率,由此即可作出二项分布概率函数的图形。下面是n,π 取不同值时的图形: 、 0.30 0.25 .s 0,5 0,0 n=7,=0.2 =7,=0.5 0.18 8 0:10 0.08 0.06 0.04 0.00 10 20 30 n=25,π=0.2
2.二项分布的图形 当n,π已知时,由(5-1)式即可计算出x = 0,1,2,.,n时的 概率,由此即可作出二项分布概率函数的图形。下面是n, π 取不同值时的图形: n=7, π=0.2 n=7, π=0.5 n=25, π=0.2