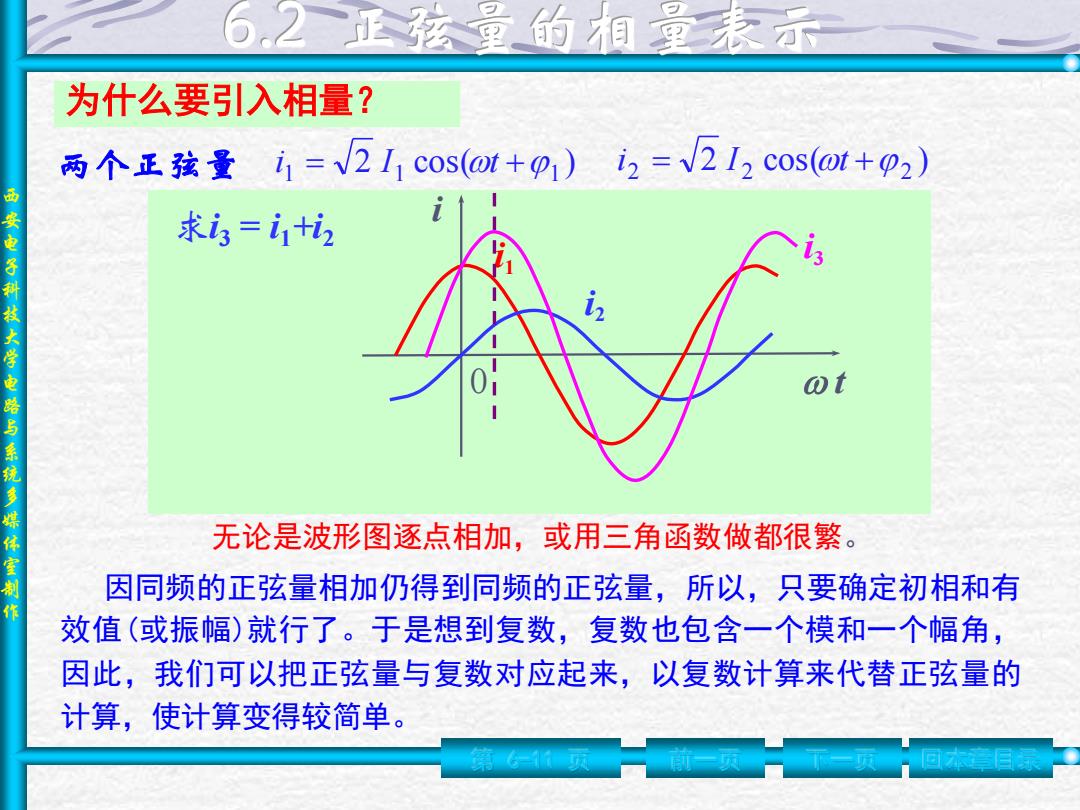
6,2正孩星的相里未示 为什么要引入相量? 两个正弦量1=V211cos(o1+p1)i2=212cos(or+p2) 求3=+2 西安电子科技大学电路与系统多媒体室制 无论是波形图逐点相加,或用三角函数做都很繁 因同频的正弦量相加仍得到同频的正弦量,所以,只要确定初相和有 效值(或振幅)就行了。于是想到复数,复数也包含一个模和一个幅角, 因此,我们可以把正弦量与复数对应起来,以复数计算来代替正弦量的 计算,使计算变得较简单
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 为什么要引入相量? 第 6-11 页 前一页 下一页 两个正弦量 i1+i2 →i3 I1 I2 I3 1 2 3 无论是波形图逐点相加,或用三角函数做都很繁。 因同频的正弦量相加仍得到同频的正弦量,所以,只要确定初相和有 效值(或振幅)就行了。于是想到复数,复数也包含一个模和一个幅角, 因此,我们可以把正弦量与复数对应起来,以复数计算来代替正弦量的 计算,使计算变得较简单。 角频率: 有效值: 初相位: 2 cos( ) 1 = 1 +1 i I t 2 cos( ) 2 = 2 + 2 i I t i1 i2 t i i1 i2 0 i3 回本章目录 求i3 = i1+i2

,2正孩里的相里求示 一、正弦量与相量 1、正弦量的相量表示 造一个复函数A0)=√2jo+p) 没有物理意义 安电子科技大学电路与系统多爆体室制作 =2lcos@1+)+j2lsin(@t+p 若对A()取实部:R[A(t)]=√2Icos@t+p)是一个正弦量,有物理意义。 对于任意一个正弦量都可以找到唯一的与其对应的复指数函数: j(@1+p) i=2Icos(@1+p)A(t)=2le A()还可以写成 )=e" 复常数→i=1e 4A①包含了三要素:、p、D,复常数包含了I,p。 称I=I∠p,为正孩量()对应的相量
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 一、正弦量与相量 第 6-12 页 前一页 下一页 1、正弦量的相量表示 造一个复函数 j( ) ( ) 2 e + = t A t I 没有物理意义 若对A(t)取实部: Re[A(t)]= 2Icos( t + ) 是一个正弦量,有物理意义。 对于任意一个正弦量都可以找到唯一的与其对应的复指数函数: j( ) 2 c ( ) ( ) 2 + = + = t i I os t A t Ie A(t)包含了三要素:I、 、 ,复常数包含了I , 。 A(t)还可以写成 t A t I j ( ) 2 e e j = 复常数 = 2Icos( t + ) + j 2Isin( t + ) j I = Ie • 回本章目录 称 I = I i 为正弦量 i(t)对应的相量。 •

6,2正弦里的相里未示 it)=√21cos(o1+p,)←→i=ILo, 相量的模表示正弦量的有效值 电 正弦量对应相量的含义 子科 相量的幅角表示正弦量的初相 加一个小圆点是用来和普通的复数相区别(强调它与正弦量的联 技大学电路与系统 系),同时也改称“相量”。相量是一个特殊的复数,它能表征一个正 弦量。复数的一切运算均适用于相量。 同样可以建立正弦电压与相量的对应关系: 多媒体室制 (0)=√2Ucos(ot+pn)←→U=ULp 将Im=Im∠p,,Um=Um∠0 称为振幅相量,其模表示正弦量的振幅。 (有效值)相量与振幅相量的关系是: im=√2i,0m=V2U 相量图(相量画在复平面上)
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 6-13 页 前一页 下一页 加一个小圆点是用来和普通的复数相区别(强调它与正弦量的联 系),同时也改称“相量” 。相量是一个特殊的复数,它能表征一个正 弦量。复数的一切运算均适用于相量。 ( ) 2 cos( ) i i i t = I t + → I = I • ( ) 2 cos( ) u U U u u t = U t + → = • 正弦量对应相量的含义 相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相 同样可以建立正弦电压与相量的对应关系: m m i Um Um u I = I = • • 将 , 称为振幅相量,其模表示正弦量的振幅。 (有效值)相量与振幅相量的关系是: I m I U m U = 2 , = 2 u i • U • I 相量图(相量画在复平面上) 回本章目录

6,2正弦量的相里未示 例1.已知 i=100V2c0s(314t+30°)A 解:i=100∠30°A u=220W2cos(314t-60°)V U=220∠-60°V 西安电子科技大学电路与系统多媒体室制作 试用相量表示i,u。 例2. 解: 已知1=50∠15°A,∫=50Hz.i=50V2cos314t+15)A 试写出电流的瞬时值表达式。 第4项
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 例1. 第 4-14 页 前一页 下一页 已知 试用相量表示 i , u 。 220 2 cos(314t 60 )V 100 2 cos(314 30 )A o o = − = + u i t 解: 220 60 V 100 30 A o o = − = • • U I 例2. 试写出电流的瞬时值表达式。 解: 50 2cos(314 15 ) A 50 15 A, 50Hz . i = t + = = • I f 已知 回本章目录

6,2正孩里的相里求示 2、相量的几何意义 我们用相量和一个正弦量对应看看它的几何意义: 01为一模为1、幅角为ot的相量。随t的增加,模不变, 安电子科技大学电路与系统多媒体室制作 而幅角与成正比,可视其为一旋转相量,当从0~T时, 相量旋转一周回到初始位置,0t从0~2π。 √2i广eo=√2e"eo'=√2lea+o)是模为√2L,初始角 度为p的旋转相量.其旋转一周在实轴上的投影即为正弦 电流i=√21cos(ot+p) 见P206图6.2.2
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2、相量的几何意义 第 6-15 页 前一页 下一页 我们用相量和一个正弦量对应看看它的几何意义: e j t 为一模为1、幅角为 t 的相量。随t的增加,模不变, 而幅角与t成正比,可视其为一旋转相量,当t从0~T时, 相量旋转一周回到初始位置, t 从0~2。 电流 。 度为 的旋转相量 其旋转一周在实轴上的投影即为正弦 是模为 初始角 2 cos( ) . 2 e 2 e e 2 2 , j j ( ) j j = + = = + • i I t I I Ie I t t t 回本章目录 见P206图6.2.2