
6,2正孩里的相里未示 二、 正弦量的相量运算 1、 同频率正弦量相加减 4()=√2U1cos(ot+p)=-Re(√21eo') 西安电子科技大学电路与系统 u2 (t)=12U2 cos(@1+2)=Re(v2U2ei) u(t)=u(t)+uz(1)=Re(v2Ue)+Re(2U2e) Rel]=Re()=Re(+) 可得共相量关集为:U=U1+U2→() 多媒体室制作 故同频的正弦量相加减运算就变成对应的相量相加减运算。 i1±2=i3 这实际上是一种变换思想。 i1±i2=i3
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 二、 正弦量的相量运算 第 4-16 页 前一页 下一页 1、 同频率正弦量相加减 故同频的正弦量相加减运算就变成对应的相量相加减运算。 这实际上是一种变换思想。 ( ) 2 cos( ) R e( 2 e ) ( ) 2 cos( ) R e( 2 e ) j 2 2 2 2 j 1 1 1 1 t t u t U t U u t U t U • • = + = = + = Re( 2 e 2 e ) Re( 2( ) e ) ( ) ( ) ( ) Re( 2 e ) Re( 2 e ) j 1 2 j 2 j 1 j 2 j 1 1 2 t t t t t U U U U u t u t u t U U • • • • • • = + = + = + = + U U U1 U2 可得其相量关系为: = + u(t) 回本章目录 i1 i2 = i3 1 2 3 I I I = Re[ 2 e ] j t U
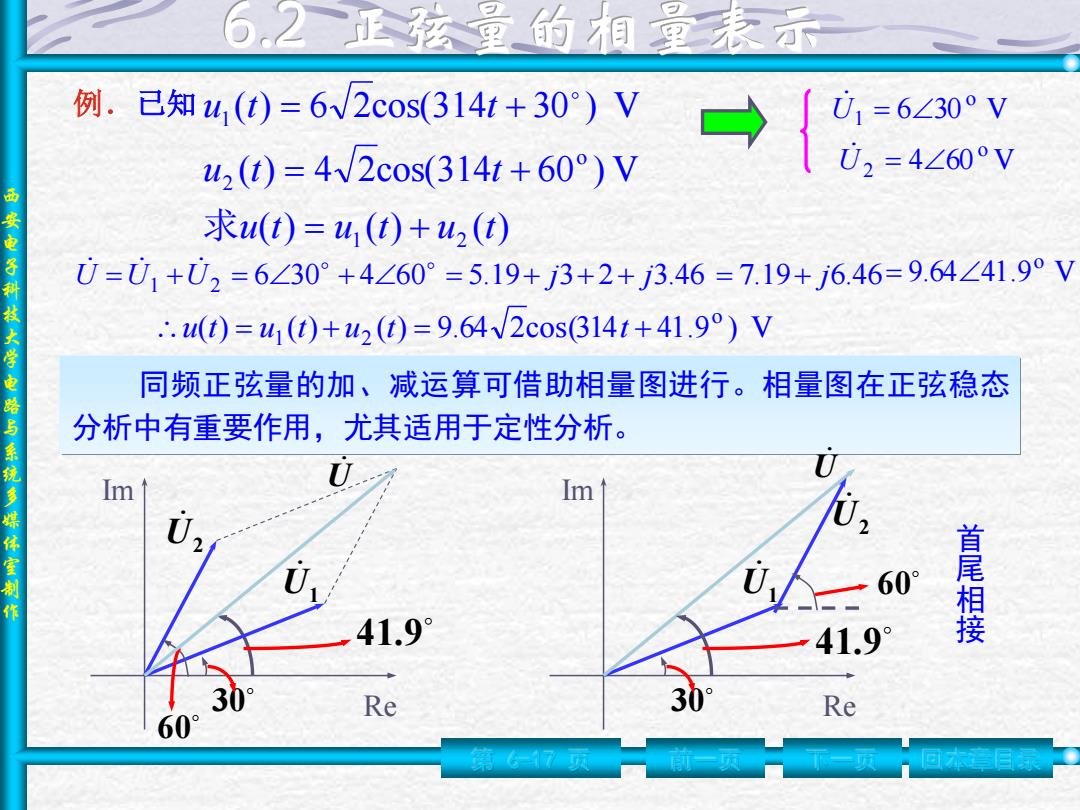
6,2正弦里的相里未示 例.已知u,(t)=6V2cos(3141+30)V U1=6∠30°V u2(t)=4W2cos(314t+60°)V 02=4∠60V 求u(t)=4(t)+u2(t) 西安电子科技大学电路与系统多媒体室制作 0-01+02=6∠30°+4∠60°=5.19+3+2+3.46=7.19+j6.46=9.64∠41.9°V ∴.()=41()+u2(①=9.64V2cos314t+41.9)V 同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态 分析中有重要作用,尤其适用于定性分析。 Im Im 60° 41.9° 首尾相接 1.9 Re 30 Re 第7项
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 例.已知 第 6-17 页 前一页 下一页 ( ) ( ) ( ) ( ) 4 2cos(314 60 ) V ( ) 6 2cos(314 30 ) V 1 2 o 2 1 u t u t u t u t t u t t = + = + = + 求 同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态 分析中有重要作用,尤其适用于定性分析。 4 60 V 6 30 V o 2 o 1 = = U U ( ) ( ) ( ) 9.64 2cos(314 41.9 ) V o u t = u1 t +u2 t = t + U =U1 +U2 = 630 + 460 Re Im 30 U1 41.9 U Re Im 41.9 30 U1 60U2 U 首 尾 相 接 = 5.19+ j3+ 2+ j3.46 = 7.19+ j6.46 9.64 41.9 V o = 60 U2 回本章目录

6,2正弦里的相里未示 2、正弦量的微分、积分运算 i=2Icos@1+)>I=IL0i 西 微分运算: 积分运算: 安电子科技大学电路与系统多媒体室制作 51oso1+,】 ∫id1=∫V21cos(o1+0,di dt =-√2Isin(ot+p,)o =√2sn(ot+p,) =V2o1c0s(@1+0,+h) =51c0s(01+9,-2 di dt →we号=ew=J0i∫a→e3=le 10 时域微分: di(t) j0i 时域积分: j0ah←→ dt 10
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2、正弦量的微分、积分运算 第 6-18 页 前一页 下一页 2 cos( ) i i i = I t + I = I ) 2 2 cos( 2 sin( ) 2 cos( ) = + + = − + = + i i i I t I t I t dt d dt di ) 2 ( ( ) d 2 cos( )d cos 2 2 sin = + − = + = + i i i t t i t I t t ω I ω I Ie e Ie j I dt di i i j j j → = = + 2 ) 2 ( j I I I idt j j j i i → = = − 2 ) 2 ( e e e 微分运算: 积分运算: j I dt di t → 时域微分 ( ) : 时域积分: → j I i t dt ( ) 回本章目录
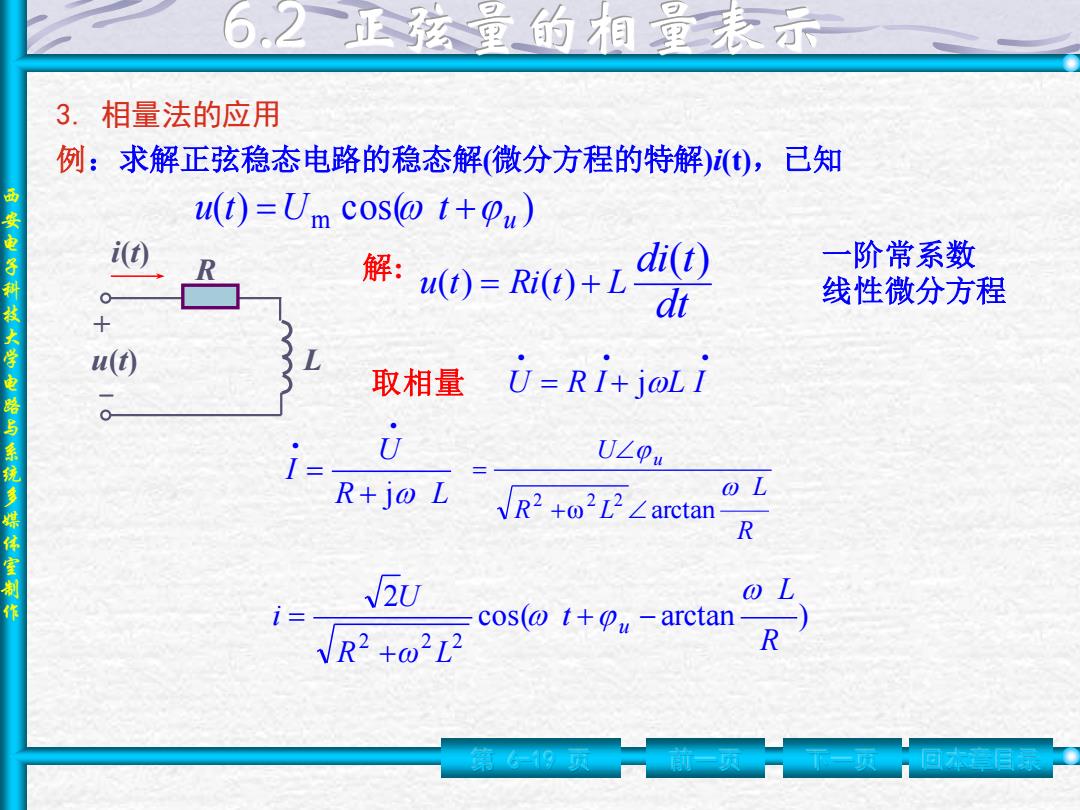
6,2正孩里的相里未示 3.相量法的应用 例:求解正弦稳态电路的稳态解(微分方程的特解)(),已知 u(t)=Um cos@1+u) 一阶常系数 西安电子科技大学电路与系统多媒体室制作 di(t) 解:0)=Ri(0+Ldi 线性微分方程 u() 取相量 U=Ri+joLi U U∠pu R+j@L √R2+o2z2∠arctan o L R 2U 1= cos(@t+-arctan VR2 +o2L2 R 68圆
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3. 相量法的应用 第 6-19 页 前一页 下一页 例:求解正弦稳态电路的稳态解(微分方程的特解)i(t),已知 ( ) m cos( ) u u t =U t + 一阶常系数 线性微分方程 R i(t) u(t) L + - dt di t u t Ri t L ( ) 解 ( ) = ( ) + : 回本章目录 • • • = + U R I jL I cos( arctan ) 2 2 2 2 R L t R ω L U i u + − + = 取相量 R L U I j + = • • R L R L U u ω arctan 2 2 2 + =
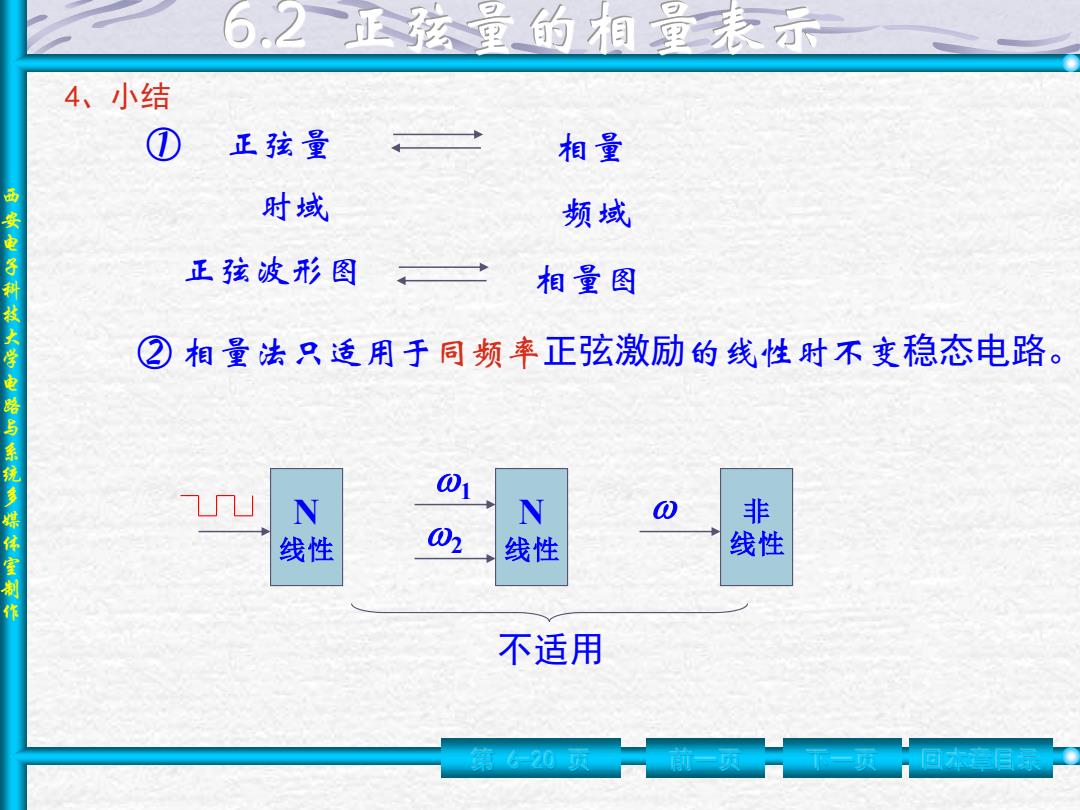
,2正弦里的相里未示 4、小结 ① 正弦量 相量 时域 频域 西安电子科技大学电路与系统多媒体室制作 正弦波形图 相量图 ②相量法只适用于同频率正弦激励的线性时不变稳态电路。 01 N N 非 线性 02 线性 线性 不适用 第620
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 4、小结 第 6-20 页 前一页 下一页 ① 正弦量 相量 时域 频域 ② 相量法只适用于同频率正弦激励的线性时不变稳态电路。 N 线性 N 线性 1 2 非 线性 不适用 正弦波形图 相量图 回本章目录