
正孩理 三、相位差(phase difference) 两个同频率的正弦波之间的相位之差称为相位差。记为日。 例如,设有相同频率的电压和电流 安电子科技大学电路与系 (t)=Ucos(ωt+pu), u,i i(t)=Imc0s(ωt+pi) 0=(ωt+0u)-(ωt+pi)=φu-pi 相位差即为初相之差 。 日仍在-≤日≤元主值范围内取值。 ●若0=0u-0>0, 多媒体室制 称电压(t)超前电流(t)0角 或(t)落后(t)0角。(比i先到达最大值) ●若0=pm-0<0, 称电压(t)落后电流(t)川日|角, 或()超前()川0|角。 行6圆
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 6-6 页 前一页 下一页 三、相位差 (phase difference) 两个同频率的正弦波之间的相位之差称为相位差。记为θ。 例如,设有相同频率的电压和电流 u(t)=Umcos(ω t + u ) , i(t) =Imcos(ωt + i ) θ= (ω t + u ) - (ωt + i ) = u - i 相位差即为初相之差。 θ仍在-π≤ θ ≤π主值范围内取值。 •若θ= u - i > 0, 称电压u(t)超前电流i(t) θ角, 或i(t)落后u(t) θ角。(u 比 i 先到达最大值); •若θ= u - i < 0, 称电压u(t)落后电流i(t) |θ|角, 或i(t)超前u(t) |θ|角。 t u, i u i u i θ 0 回本章目录
正孩理 几种特殊相位关系: u,i ·若0=04-0=0, 西 称电压(①)与电流()同相。 安电子科技大学电路与系统 ●若0=04-0;=士π, 称电压(0与电流i①反相 ·若0=04-0=±π/2, 称电压()与电流(t)正交。 多媒体室制作 u,i 注意:0=π/2:u超前iπ/2,不说u 落后i3π/2;i落后uπ/2,不说i超 01 前u3元/2。主值范围0≤元
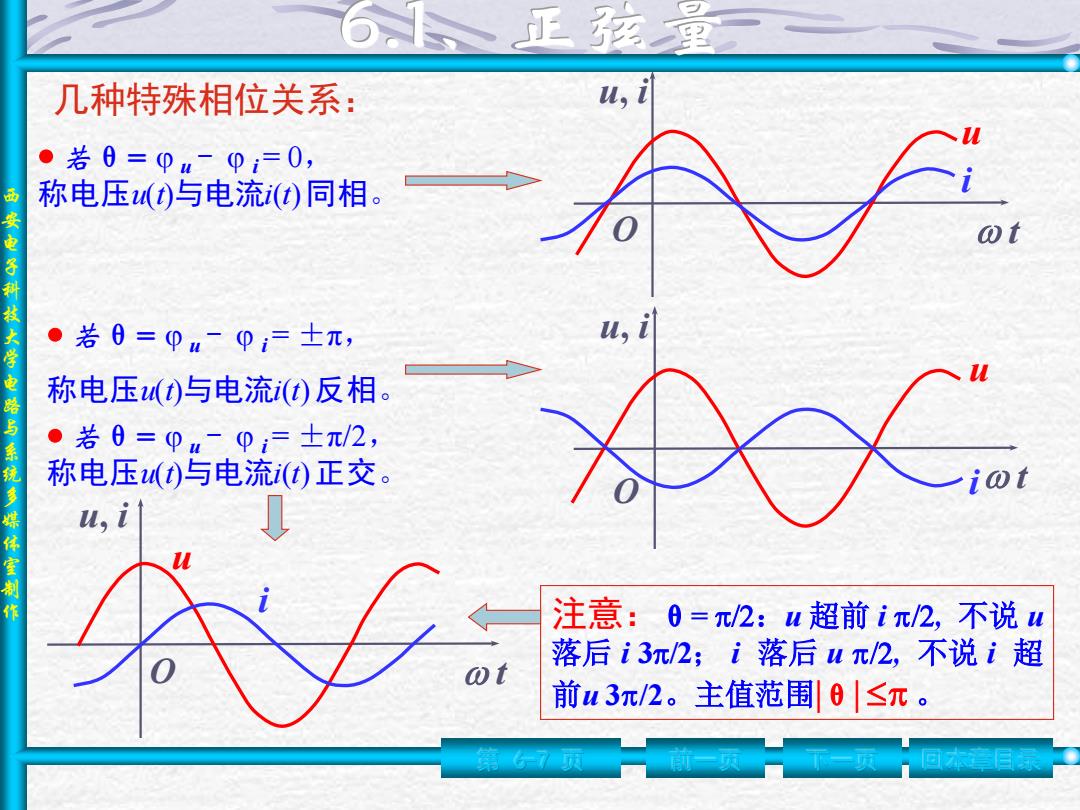
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 几种特殊相位关系: 第 6-7 页 前一页 下一页 • 若θ= u - i = ±π, 称电压u(t)与电流i(t) 反相。 t u, i u i O • 若θ= u - i = 0, 称电压u(t)与电流i(t) 同相。 • 若θ= u - i = ±π/2, 称电压u(t)与电流i(t) 正交。 t u, i u O i t u, i u i O 注意:θ= /2:u 超前 i /2, 不说 u 落后 i 3/2; i 落后 u /2, 不说 i 超 前u 3/2。主值范围|θ| 。 回本章目录
6,2正弦量的相量表示 为求正弦稳态响应,1893年斯台麦兹首先把复数理论用于电路,从而 为分析电路的正弦稳态响应提供了有力的工具。运用复数分析电路的方法 称为相量法(phasor method).。 复数的有关知识复习 安电子科技大学电路与系统多媒体室制作 虚数单位j=√-1 1.复数的表示 b A A 直角坐标:A=a+jb A 极坐标:A=Alej0=A∠0 a Re (a)复平面表示的复数 (b)简画法 两种表示法之间的关系: 1AVa2+b2 a=4l cose b 0 arctan b=Alsine a
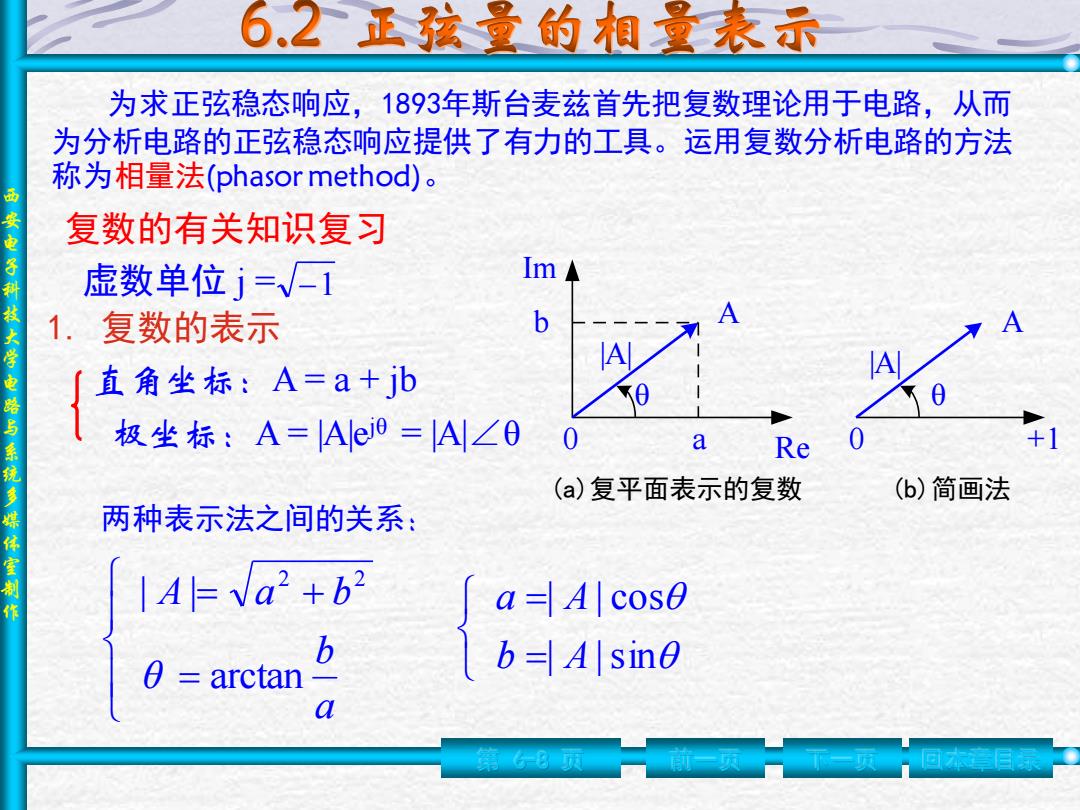
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 为求正弦稳态响应,1893年斯台麦兹首先把复数理论用于电路,从而 为分析电路的正弦稳态响应提供了有力的工具。运用复数分析电路的方法 称为相量法(phasor method)。 第 6-8 页 前一页 下一页 复数的有关知识复习 虚数单位 j = −1 1. 复数的表示 直角坐标:A = a + jb 极坐标:A = |A|ejθ = |A|∠θ Re Im 0 a b |A| θ θ |A| A A 0 +1 (a)复平面表示的复数 (b)简画法 两种表示法之间的关系: = = + a b θ A a b arctan | | 2 2 = = | |sin | | cos b A a A 回本章目录
6,2正弦里的相里未示 2.复数的运算 Im ()如减运算— 直角坐标 A+B 若 A1=41+jb1,A2=2+jb2 A-B 安电子科技大学电路与系统多媒体室制 则 A1±A2=(a1±2)+j(b1±b2) B (2) 乘除运算 极坐标 Re 若A1=A101,若A2=A2102 -B 则 符合平行四边形法则 AA=4le94le=44lea+o,)=44l∠0,+0, 4l∠014le9-Ae0rg)=41∠01-02 A2 141∠021421e02|A2' |A2
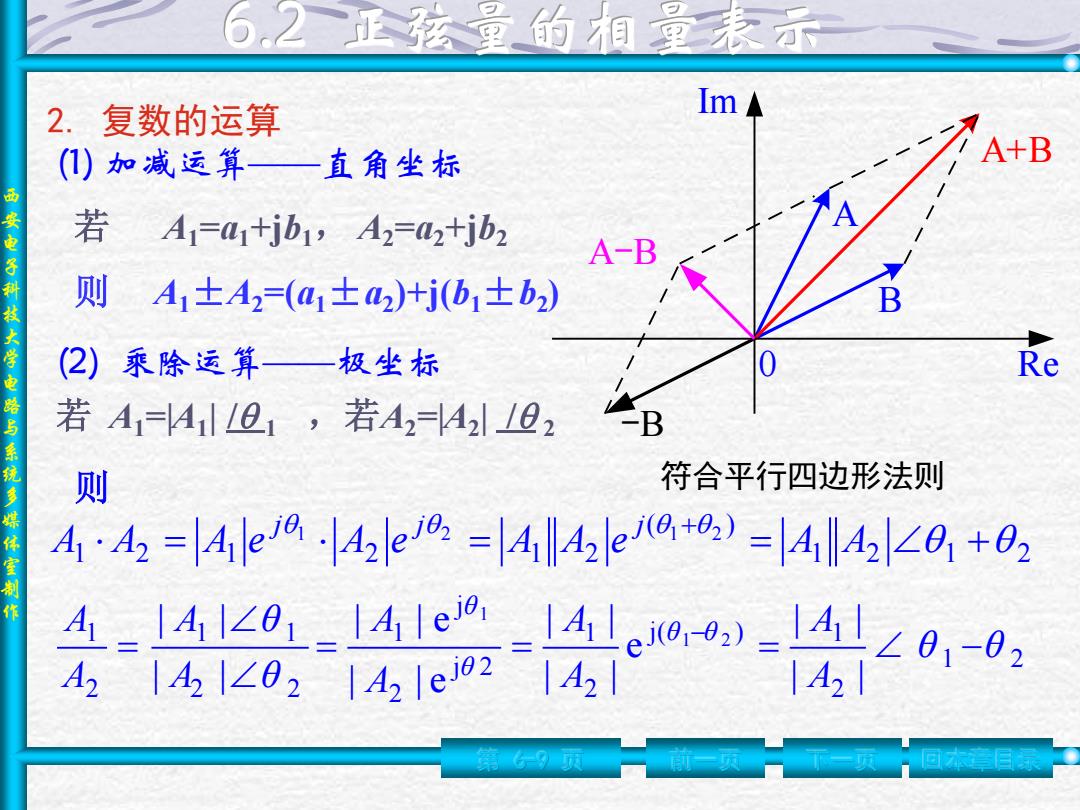
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2. 复数的运算 第 6-9 页 前一页 下一页 (1) 加减运算——直角坐标 若 A1=a1+jb1, A2=a2+jb2 则 A1±A2=(a1±a2 )+j(b1±b2 ) Re Im 0 A+B A B 符合平行四边形法则 -B A-B (2) 乘除运算——极坐标 若 A1=|A1 | / 1 ,若A2=|A2 | / 2 1 2 1 2 ( ) 1 2 1 2 1 2 1 2 1 2 = = = + + A A A e A e A A e A A j j j 则 1 2 2 j ( ) 1 2 1 j 2 2 j 1 2 2 1 1 2 1 | | | | e | | | | | | e | | e | | | | 1 2 1 θ θ A A A A A A A θ A θ A A θ θ θ θ = = = − = − 回本章目录

6,2正弦里的相里未示 (3)几种常用关系: j2=-1,j3=-j,j4=1,1/j=j 西安电子科技大学电路与系统多媒体室制作 e90°=j,ej0°=j,e±j180°=-1 1+j=W2∠45°1-j=V2∠-45° -1+j=V2∠135° -1-j=V2∠-135° 1+2=V5∠63.4° 2+1=V5∠26.6° 第610员
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 6-10 页 前一页 下一页 j 2 = -1 , j3 = -j , j4 = 1 , 1/j = -j e j90°= j , e -j90°= -j , e ±j180°= -1 回本章目录 (3) 几种常用关系: − + = − − = − + = − = − 1 2 135 1 2 135 1 2 45 1 2 45 j j j j 1+ j2 = 563.4 2 + j1 = 526.6