
第二章电阻电路的一般分析方法 将仅包含电阻、独立源和受控源的电路称为电阻电路。 2.1图与电路方程 一、网络(电路)的拓扑图 西安电子科技大学电路与系统多媒体室制作 二、回路、割集、树 三、KCL和KVL的独立方程 2.22b法和b法 一、2b法一 二、b法 2.3回路法与网孔法 一、回路法 二、网孔法 2.4割集法与节点法 割集法 节点法 出 点击目录,进入和关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 点击目录 ,进入相关章节 2.1 图与电路方程 一、网络(电路)的拓扑图 二、回路、割集、树 三、KCL和KVL的独立方程 2.2 2b法和b法 一、2b法 二、b法 2.3 回路法与网孔法 一、回路法 二、网孔法 2.4 割集法与节点法 一、割集法 二、节点法 第 2-1 页 前一页 下一页 退出本章 将仅包含电阻、独立源和受控源的电路称为电阻电路

2.1图与电路方程 网终(电路的拓扑图 1、图的定义: 将电路中每一条支路画成抽象的线段所形成的一个节点 西 和支路集合称为拓扑图,简称为图,记为G。 图中的线段就是图的支路(也称为边),线段的连接点是 图的节点(也称为顶点),用黑点表示。注意:电路的支路 安电子科技大学电路与系统多媒体室制作 是实体,而图的支路是抽象的线段。 +1S5 Rs 4 b R2 (a)电路 (b)图 图(b)的图有四个节点(a、b、c、d和6条支路(1,2,3,4,5,6) 回目
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2.1 图与电路方程 将电路中每一条支路画成抽象的线段所形成的一个节点 和支路集合称为拓扑图,简称为图,记为G。 图中的线段就是图的支路(也称为边),线段的连接点是 图的节点(也称为顶点),用黑点表示。注意:电路的支路 是实体,而图的支路是抽象的线段。 i4 R1 uS2 uS5 R2 R3 R4 R5 R6 2i4 (a)电路 (b)图 a b c d 1 2 3 4 5 6 图(b)的图有四个节点(a、b、c、d)和6条支路(1,2,3,4,5,6) 第 2-2 页 前一页 下一页 返回本章目录 1、图的定义:
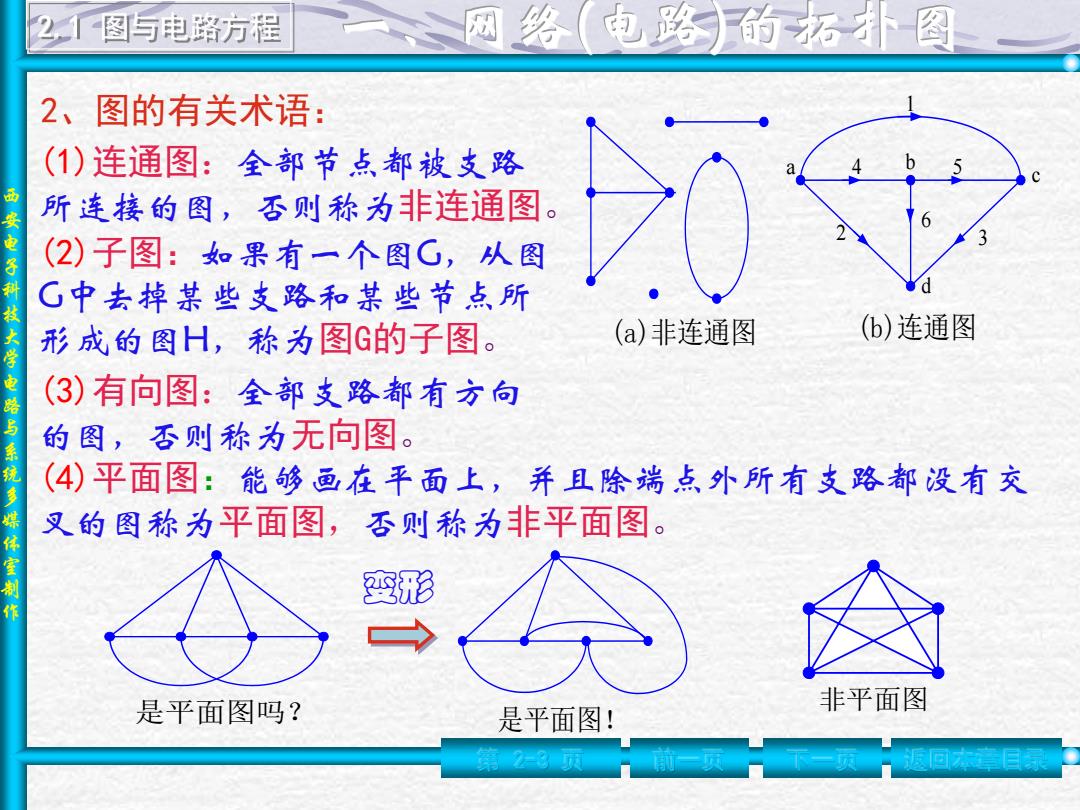
2图与电路方程 网络(电路的拓补图 2、图的有关术语: ()连通图:全部节点都被支路 所连接的图,否则称为非连通图 电子 (2)子图:如果有一个图G,从图 G中去掉某些支路和某些节点所 大学 形成的图H,称为图G的子图。 (a)非连通图 (b)连通图 电路 (3)有向图:全部支路都有方向 的图,否则称为无向图。 纯多 (④)平面图:能够画在平面上,并且除端点外所有支路都设有交 媒体室制 叉的图称为平面图,否则称为非平面图。 变形 是平面图吗? 非平面图 是平面图! 回目
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2.1 图与电路方程 (1)连通图:全部节点都被支路 所连接的图,否则称为非连通图。 (b)连通图 a b c d 1 2 3 4 5 6 (a)非连通图 (3)有向图:全部支路都有方向 的图,否则称为无向图。 (2)子图:如果有一个图G,从图 G中去掉某些支路和某些节点所 形成的图H,称为图G的子图。 (4)平面图:能够画在平面上,并且除端点外所有支路都没有交 叉的图称为平面图,否则称为非平面图。 是平面图吗? 是平面图! 非平面图 变形 第 2-3 页 前一页 下一页 返回本章目录 2、图的有关术语:
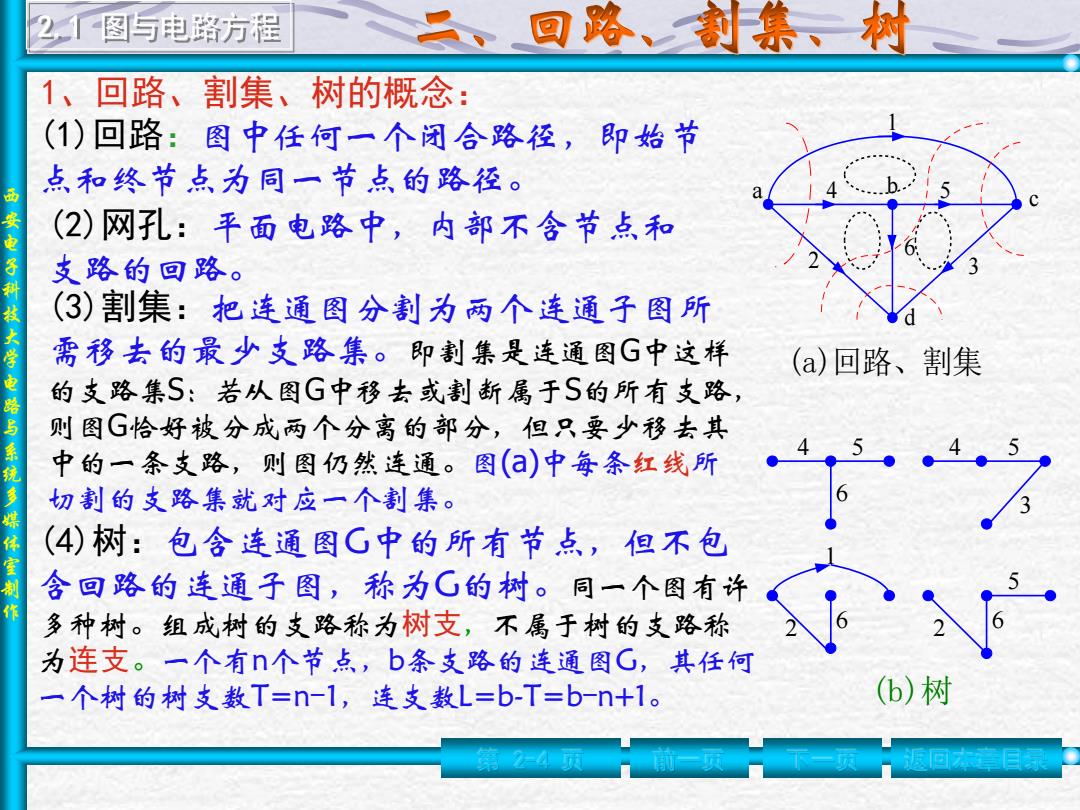
2图与电路方程 回路、割集、树 、回路、割集、树的概念: (1)回路:图中任何一个闭合路径,即始节 点和终节点为同一节点的路径。 电 (2)网孔:平面电路中,内部不含节点和 子 支路的回路。 (3)割集:把连通图分割为两个连通子图所 大学 需移去的最少支路集。即割集是连通图G中这样 (a)回路、割集 电 的支路集S:若从图G中移去或割断属于S的所有支路, 则图G恰好被分成两个分离的部分,但只要少移去其 系统 中的一条支路,则图仍然连通。图()中每条红线所 切割的支路集就对应一个割集。 (4)树:包含连通图G中的所有节点,但不包 制 含回路的连通子图,称为C的树。同一个图有许 多种树。组成树的支路称为树支,不属于树的支路称 为连支。一个有n个节点,b条支路的连通图G,其任何 一个树的树支数T=n-1,连支数L=b-T=b-n+1。 (b)树 4万
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 (1)回路:图中任何一个闭合路径,即始节 点和终节点为同一节点的路径。 (3)割集:把连通图分割为两个连通子图所 需移去的最少支路集。即割集是连通图G中这样 的支路集S:若从图G中移去或割断属于S的所有支路, 则图G恰好被分成两个分离的部分,但只要少移去其 中的一条支路,则图仍然连通。图(a)中每条红线所 切割的支路集就对应一个割集。 (4)树:包含连通图G中的所有节点,但不包 含回路的连通子图,称为G的树。同一个图有许 多种树。组成树的支路称为树支,不属于树的支路称 为连支。一个有n个节点,b条支路的连通图G,其任何 一个树的树支数T=n-1,连支数L=b-T=b-n+1。 (a)回路、割集 a b c d 1 2 3 4 5 6 4 5 6 5 3 1 2 6 5 6 2 4 (b)树 (2)网孔:平面电路中,内部不含节点和 支路的回路。 第 2-4 页 前一页 下一页 返回本章目录 1、回路、割集、树的概念: 2.1 图与电路方程
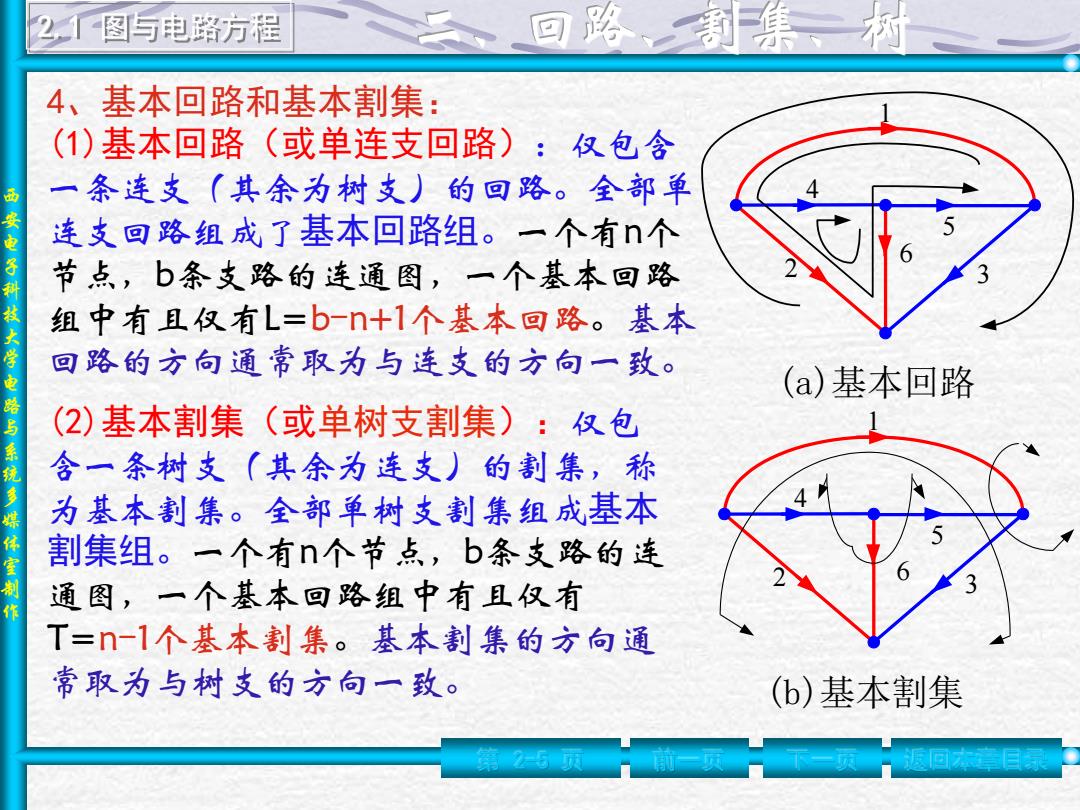
2图与电路方程 回路莉集、州 4、基本回路和基本割集: ()基本回路(或单连支回路):仅包含 一条连支(其余为树支)的回路。全部单 安电 连支回路组成了基本回路组。一个有n个 子 节点,b条支路的连通图,一个基本回路 技 组中有且仅有L=b-n+1个基本回路。基本 大学 回路的方向通常取为与连支的方向一致。 (a)基本回路 路与 (2)基本割集(或单树支割集):仅包 系统 会一条树支(其余为连支)的割集,称 多 为基本割集。全部单树支割集组成基本 体室 割集组。一个有n个节点,b条支路的连 通图,一个基本回路组中有且仅有 T=-1个基本割集。基本割集的方向通 常取为与树支的方向一致。 (b)基本割集
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 (1)基本回路(或单连支回路):仅包含 一条连支(其余为树支)的回路。全部单 连支回路组成了基本回路组。一个有n个 节点,b条支路的连通图,一个基本回路 组中有且仅有L=b-n+1个基本回路。基本 回路的方向通常取为与连支的方向一致。 (2)基本割集(或单树支割集):仅包 含一条树支(其余为连支)的割集,称 为基本割集。全部单树支割集组成基本 割集组。一个有n个节点,b条支路的连 通图,一个基本回路组中有且仅有 T=n-1个基本割集。基本割集的方向通 常取为与树支的方向一致。 (a)基本回路 1 2 3 4 5 6 (b)基本割集 1 2 3 4 5 6 第 2-5 页 前一页 下一页 返回本章目录 4、基本回路和基本割集: 2.1 图与电路方程