
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的应用一火箭遥测数据处理 10 100 000 0 ZH/J 000 443020 -10 0 0 20 40 6080100120140 20 40 60 80 100 120 t/s t/s 图1某发火箭遥测参数时域曲线 图4遥测数据0140s时频分析图
STFT的应用—火箭遥测数据处理 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换
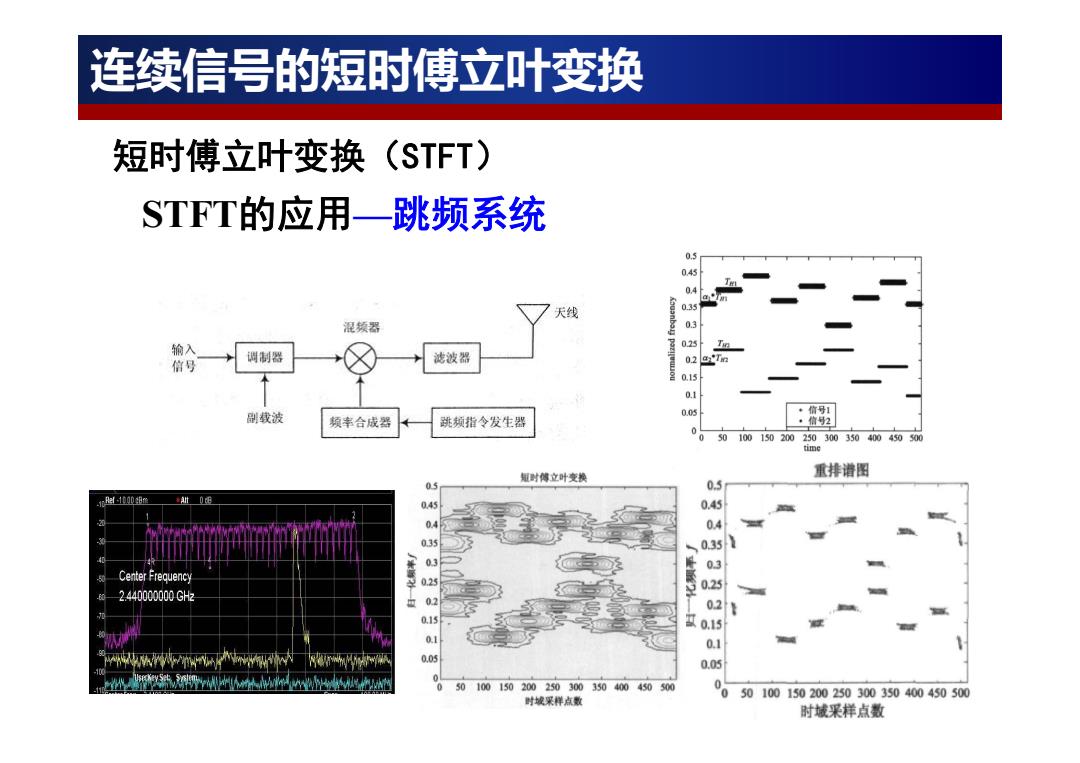
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的应用一跳频系统 0.5 0 04 天线 混领器 03 输入 023 信号 调制器 滤波器 02 015 副载波 ·值号1 频率合成器 跳烦指令发生器 ·信号2 005010015020025030035040045030 time 显时傅立叶变换 重排谱图 05 05 045 04 0.35 Center Frequency 3 2.440000000GH2 02 0.1 0.05 50100150200250300350400450500 时城采样点数 )50100150200250300350400450500 时城采样点数
STFT的应用—跳频系统 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换

连续信号的短时傅立叶变换 短时傅立叶变换(STFT) 随堂练习 求x(t)=Asint的STFT,窗函数8(t)=1
求 的STFT,窗函数 0 xt A t ( ) sin g t() 1 随堂练习 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换

连续信号的短时傅立叶变换 谱图(spectrogram) STFT,(t,)x(r)g(r-t)e dr P=S,(t,2) 式中S,(t,2)称为⑥的谱图。该式为信号的“双线性”或 “二次”时一频分布。由于‖g(x)川=1 所以∬S,(t,2)dd2=E 即谱图是信号能量的分布。 例6令x)=ear为chirp信号,M)=代t-T) 为一高斯窗,式中#都是常数。x(t)的谱图是: S,,2)S7FT,,2)P=(4a)"exp(-an)
式中 称为 的谱图。该式为信号的“双线性”或 “二次”时-频分布。由于 所以 即谱图是信号能量的分布。 例6 令 为chirp 信号, 为一高斯窗,式中 都是常数。 的谱图是: 2 2 | ( , )| | ( ) ( ) | ( , ) j x x STFT t x g t e d S t || ( ) || 1 g (, ) x x S t dtd E 2 ( ) j t xt e 0 x() ( ) 0 0 0 (,)()() () j j xSTFTt gtedgte x(t) 2 2 2 24 24 2 1/2 4 ( 2) 14 14 ( , ) | ( , ) | ( ) exp( ) t x x S t STFT t S ( t, ) x x( )t 谱图(spectrogram) 连续信号的短时傅立叶变换

连续信号的短时傅立叶变换 谱图(spectrogram) S,(G,2)S7FT,t,2)P=(a)exp(-i0,) 1+4a2.4 显然,当2=2t时,S(t,2)最大。所以S,(t,2)图形集 中在=2的斜线上。也即x(t)的能量分布在这条斜线 上。由于x(t)=eoo,而p(t)=at2,所以p'(t)=2ot,这 就是x(t)的瞬时频率。也即x(t)的能量主要分布在其瞬 时频率的“轨迹”上
显然,当 时, 最大。所以 图形集 中在 的斜线上。也即 的能量分布在这条斜线 上。由于 ,而 ,所以 ,这 就是 的瞬时频率。也即 的能量主要分布在其瞬 时频率的“轨迹”上。 2 t S ( t, ) x S ( t, ) x 2 t x ( t ) x ( t ) ( ) ( ) j t x t e 2 ( t ) t ( t ) 2 t x ( t ) ( , ) | ( , ) | ( ) exp( 2 4 ) 2 2 2 4 2 1 4 ( 2 ) 1 4 2 4 t x x S t STFT t 谱图(spectrogram) 连续信号的短时傅立叶变换