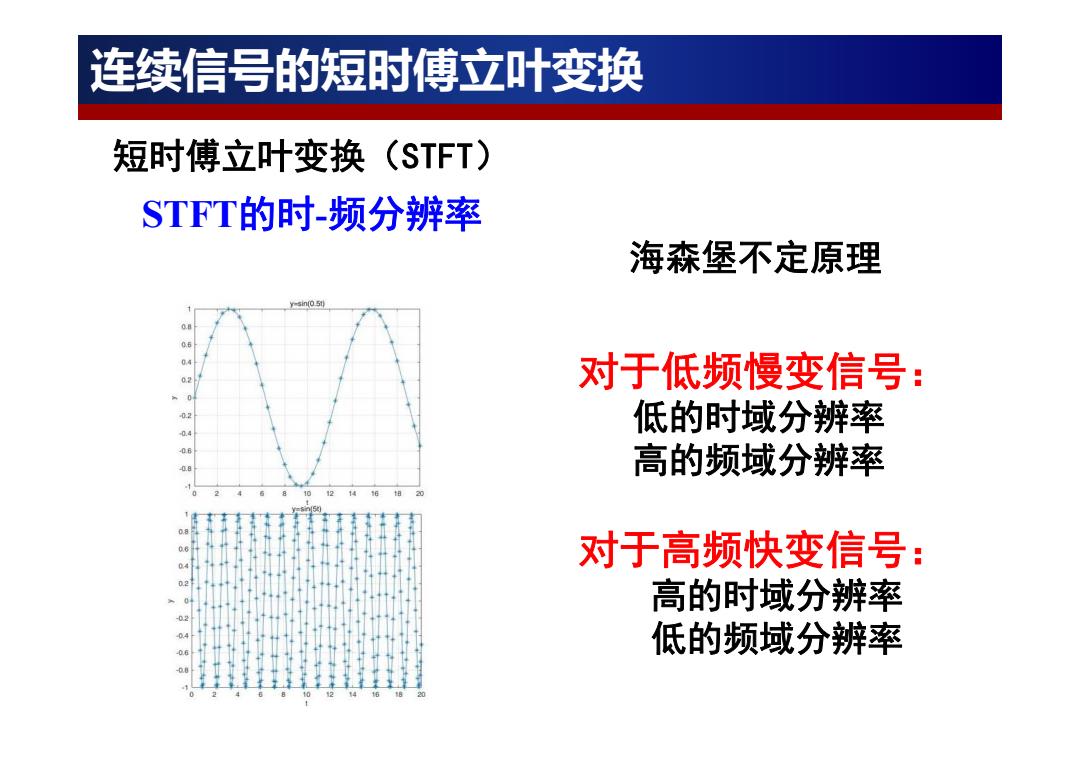
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的时-分辨率 海森堡不定原理 rsn05到 对于低频慢变信号: 0 低的时域分辨率 高的频域分辨率 对于高频快变信号: 高的时域分辨率 低的频域分辨率
对于低频慢变信号: 低的时域分辨率 高的频域分辨率 对于高频快变信号: 高的时域分辨率 低的频域分辨率 海森堡不定原理 STFT的时 -频分辨率 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换

连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的时-频分辨率 例1:令x(T)=6(t-to) 则其STFT为 STFT,(t,)=6(r-To)g(r-t)e-dr =g(to-t)e- 该例说明,STFT的时间分辨率由窗函数g()的宽度而决定。 例2:若x(x)=e2 STFT(t,)=[eg(-t)e-dr=G(Q-Q)e- 因此,STFT的频率分辨率由g(t)频谱的宽度来决定
例2: 若 因此,STFT的频率分辨率由 频谱的宽度来决定。 则其STFT为 该例说明,STFT的时间分辨率由窗函数 的宽度而决定。 ( ) ( ) 0 x 0 0 0 (, ) ( ) ( ) ( ) j j x STFT t g t e d g t e g( ) 例1: 令 0 0 ( ) 0 (, ) ( ) ( ) j jt j x STFT t e g t e d G e g( ) 0 ( ) j x e STFT的时-频分辨率 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换

连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的时-频分辨率 例3若g(x)=1H则G(2)=6(2) 则其STFT变换为 Signal in time 0.5 STFT.(t,2)=X(2) -0.5 Linear scale ISTFT,Lh=63,Nf=64,lin.scale,contour,Thld=5% 0.4 0.3 0.2 0.1 16884 20 40 6080 100 120 Time [s] STFT无任何时域定位功能
-0.5 0 0.5 Real part Signal in time 168 84 0 Linear scale Energy spectral density 20 40 60 80 100 120 0 0.1 0.2 0.3 0.4 |STFT|2, Lh=63, Nf=64, lin. scale, contour, Thld=5% Time [s] Frequency [Hz] 例3 若 ,则 则其STFT变换为 g( ) 1 G() () STFT (t,) X () x STFT无任何时域定位功能 STFT的时-频分辨率 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换
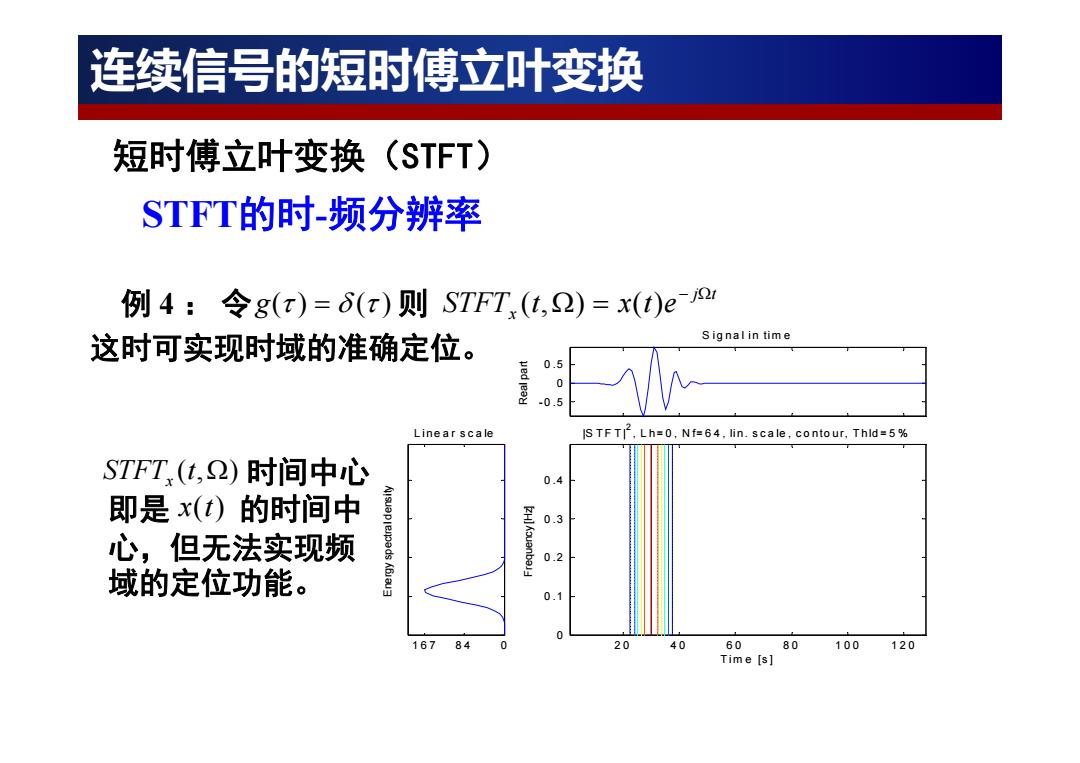
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的时-分辨率 例4:令g(x)=6(x)则STFT(t,2)=x(t)o 这时可实现时域的准确定位。 Signalin time 0.5 .0.5 Linear scale IS TFT2,Lh=0,Nf=64.lin.scale,contour,Thld=5% STFT(t,2)时间中心 0.4 即是x(t)的时间中 0.3 心,但无法实现频 0.2 域的定位功能。 0.1 167 84 20 40 60 80 100 120 Time [s]
-0 .5 0 0 .5 Real part S ig na l in tim e 167 8 4 0 L ine a r s c a le Energy spectral density 2 0 4 0 6 0 8 0 100 120 0 0 .1 0 .2 0 .3 0 .4 |S T F T |2 , L h= 0 , N f= 6 4 , lin. s c a le , c o nto ur, T hld = 5 % Tim e [s] Frequency [Hz] 例 4 :令 则 这时可实现时域的准确定位。 g( ) ( ) j t x STFT t x t e ( ,) ( ) STFT (t,) x x(t) 时间中心 即是 的时间中 心,但无法实现频 域的定位功能。 STFT的时-频分辨率 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换
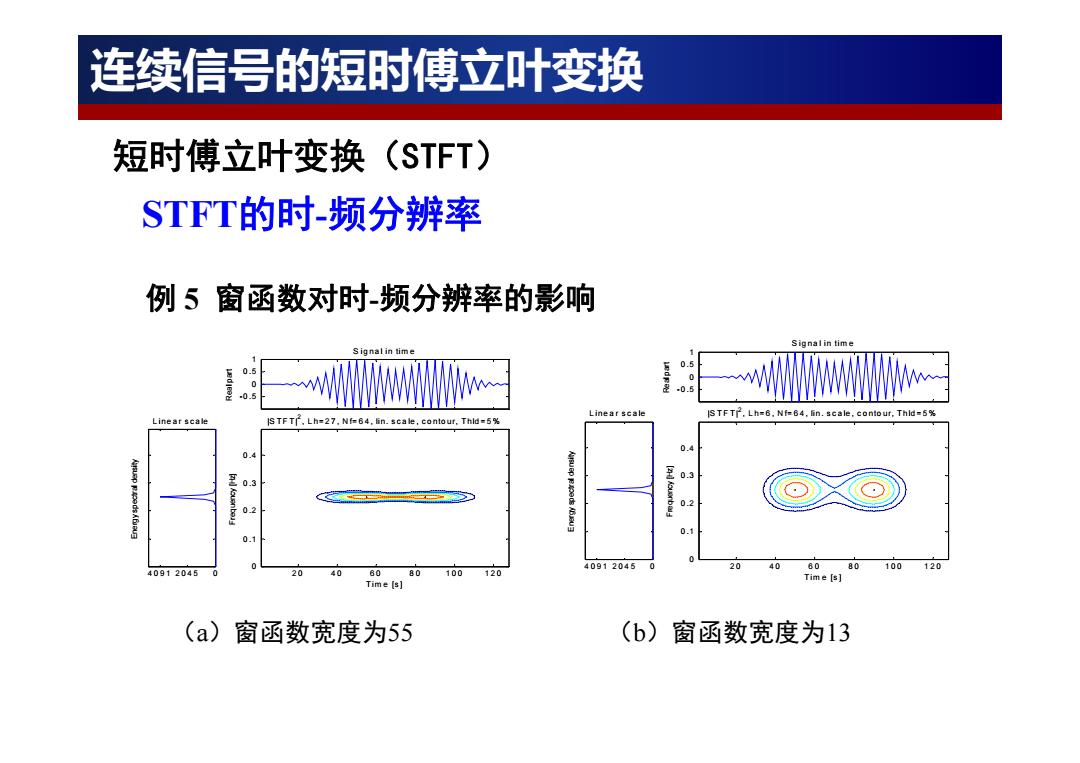
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT的时-分辨率 例5窗函数对时频分辨率的影响 Signalin time Signalin time 0.5 0.5 0.5 0 Linear scale STFT.Lh=6.Nf-64,lin.scale,contour.Thld=5% Linear scale IS TFT,Lh=27,Nf-64,lin.scale,contour,Thld=5% 04 0.4 0.3 0.3 0.2 02 0.1 0 40912045 20 40 80 80 100 120 40912045 20 4060 80 100 120 Time [s] Time【s] (a) 窗函数宽度为55 (b)窗函数宽度为13
例 5 窗函数对时-频分辨率的影响 -0.5 0 0.5 1 Real part S ig na l in tim e 4091 2045 0 L ine a r s c a le Energy spectral density 2 0 4 0 6 0 8 0 100 120 0 0.1 0.2 0.3 0.4 |S T F T |2 , L h= 2 7 , N f= 6 4 , lin. s c a le , c o nto ur, Thld = 5 % Tim e [s] Frequency [Hz] -0 .5 0 0 .5 1 Real part S ig na l in tim e 4091 2045 0 L ine a r s c a le Energy spectral density 2 0 4 0 6 0 8 0 100 120 0 0 .1 0 .2 0 .3 0 .4 |S T F T |2 , L h= 6 , N f= 6 4 , lin. s c a le , c o nto ur, Thld = 5 % Tim e [s] Frequency [Hz] (a)窗函数宽度为55 (b)窗函数宽度为13 STFT的时-频分辨率 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换