
定理2n个元素(n>1)共有n!个n级排列,其中奇、偶 排列各占一半,即各有n/2个. 证明设这n!个n级排列中共有s个奇排列,个偶排列, 现证s=t. s个奇排列 前两个数对换 s个偶排列所以s≤t t个偶排列 前两个数对换 t个奇排列所以t≤s 故必有S=t
证明 设这n!个n级排列中共有s个奇排列,t个偶排列, 现证s=t. 故必有 s = t. 奇排列 偶排列 所以 s t ≤ 前两个数对换 s个 s个 偶排列 奇排列 所以 t s ≤ 前两个数对换 t个 t个 定理2 n个元素(n>1)共有n!个n级排列,其中奇、偶 排列各占一半,即各有 n!/ 2 个
三、n阶行列式 1.分析三阶行列式结果 =011022433+012423431+013021432 -L1322M31-L12L21L33-11L2332· 归纳每项内容及符号的规律 (1)每项都是位于不同行不同列的三个元素的乘积. 三阶行列式共有6项,即3!项. (2)符号:当行标按1,2,3排列时,每项都可写成 a1022a35 每项符号决定于列标排列的逆序数,即(-1)) 其中1J2J3为列标全排列
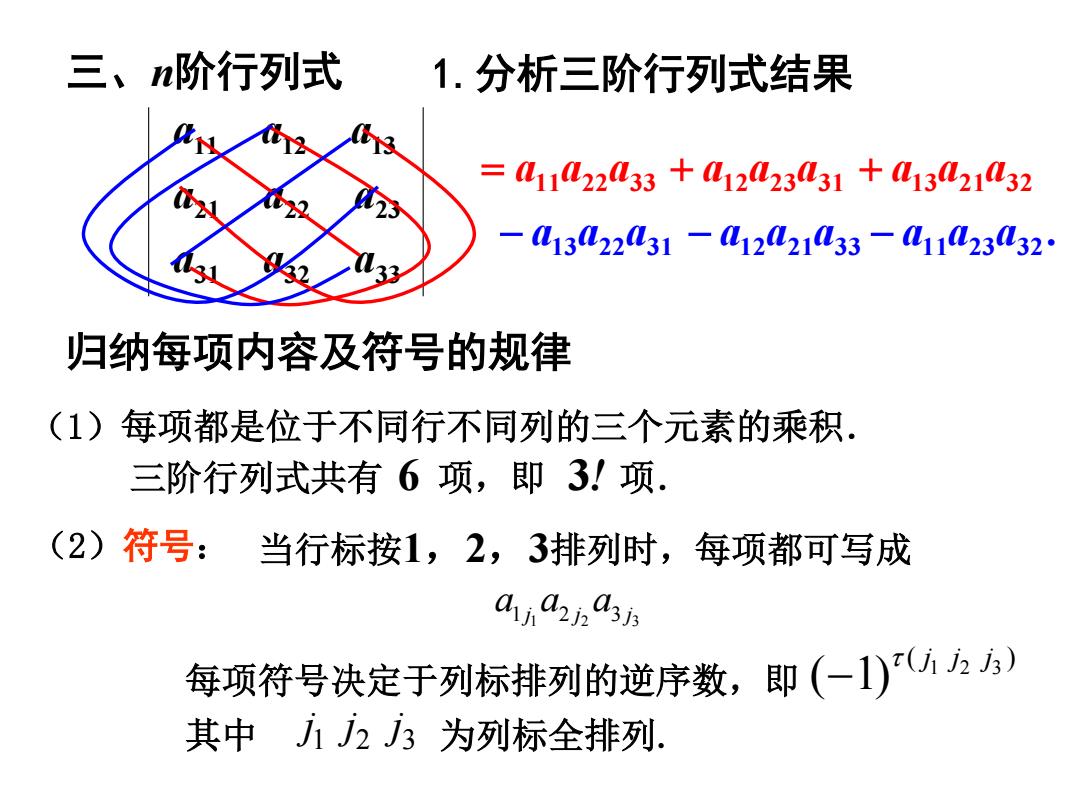
1.分析三阶行列式结果 归纳每项内容及符号的规律 三阶行列式共有 6 项,即 3! 项. (1)每项都是位于不同行不同列的三个元素的乘积. 三、n阶行列式 31 32 33 21 22 23 11 12 13 a a a a a a a a a = a11a22a33 . − a11a23a32 + a12a23a31 + a13a21a32 − a13a22a31 − a12a21a33 (2)符号: 当行标按1,2,3排列时,每项都可写成 每项符号决定于列标排列的逆序数,即 123 ( ) ( 1)τ jj j − 其中 123 为列标全排列. jj j 123 12 3 jjj aa a

综上,三阶行列式 C411 412 a3 D3= 021 22 C23 ∑(-1)ihaa2a (1j23) a31 a32 33 ∑ 为对列标所有全排列求和· (j1j2j3)
综上,三阶行列式 123 123 123 11 12 13 ( ) 3 21 22 23 1 2 3 ( ) 31 32 33 ( 1) jj j jjj jj j aaa D a a a aa a aaa τ = = − ∑ ∑ 为对列标所有全排列求和 . ( ) 1 2 3 j j j

2. n阶行列式 定义 1 012 n D 022 02n =∑(-1-aa6…a (jj2…jn 【注】 由n2个数构成,有n行、n列,ai 称为行列式的元素. 2°为所有不同行不同列的n个数乘积的代数和,共n!项. 3°当行标按1,2,,排列时,每项符号决定于列标 排列的奇偶性:偶排列取正号,奇排列取负号. 4·n阶行列式简记作det(a,)(determinant),或a, 5。一阶行列式a=不要与绝对值记号相混淆
定义 2. n阶行列式 1°由 个数构成,有n行、n列, 称为行列式的元素. ij a 2 n 2°为所有不同行不同列的n个数乘积的代数和,共 n!项 . 3°当行标按1,2,…,n排列时,每项符号决定于列标 排列的奇偶性:偶排列取正号,奇排列取负号. 4 ° n阶行列式简记作 det( ) aij (determinant) ,或 ij a ( ) ( 1 2 ) 1 2 1 2 11 12 1 21 22 2 1 2 ( ) 1 2 1 n n n n n jj j j j nj jj j n n nn aa a aa a D aa a aa a τ = = − ∑ 【注】 5 °一阶行列式 a = a不要与绝对值记号相混淆

例5有4阶行列式,分析: (1)a21a32a43a14 (2)a12a2314a31 (3)a21a32a43414422 是否为展开式中的一项,若是,确定其在展开式中 的符号. 例6计算n阶行列式(其中a≠0,i=1,2,n ) 02 0 0 0 0n3 【注】该行列式中左上角到右下角的对角线称为 主对角线,主对角线上的各元素称为主对角元素. 称左侧的行列式为下三角形行列式,右侧的行列 式为上三角形行列式
例5 有4阶行列式,分析: (1) 是否为展开式中的一项,若是,确定其在展开式中 的符号. 21 32 43 14 12 23 14 31 21 32 43 14 22 a a a a (2)a a a a (3)a a a a a 11 21 22 123 00 0 0 0 n n n nn a a a aaa a 【注】该行列式中左上角到右下角的对角线称为 主对角线,主对角线上的各元素称为主对角元素. 称左侧的行列式为下三角形行列式,右侧的行列 式为上三角形行列式. 例6 计算n阶行列式(其中 ai n ii ≠ = 0, 1,2,... ) 11 12 1 22 2 0 0 0 0 0 ... n n nn aa a a a a =