
飞号与系型 §8.5z变换的基本性质 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §8.5 z变换的基本性质

主要内容 线性 位移性 序列线性加权 序列指数加权 初值定理 终值定理 时域卷积定理 域卷积定理( 自阅
X 第 2 主要内容 页 线性 位移性 序列线性加权 序列指数加权 初值定理 终值定理 时域卷积定理 z域卷积定理(自阅)

线性 (表现为叠加性和均匀性) 若 Z[x(]=X(a) Rs <<Rv2) Zy(n】=Y(a) R<<R2) 则 Zlax(n)+bv(n)]=ax(z)+bY(z)(R <R2) 4,b为任意常数。 ROC:一般情况下,取二者的重叠部分 max(R,R)<<min(Rx2,Ry2) 某些线性组合中某些零点与极点相抵消,则收敛域可能扩 大。 刨题 倒题
X 第 3 一.线性 页 a,b为任意常数。 ( ) ( ) ( ) 1 2 1 2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Z ax n by n aX z bY z R z R Z y n Y z R z R Z x n X z R z R y y x x + = + = = 则 若 ROC:一般情况下,取二者的重叠部分 max( , ) min( , ) x1 y1 Rx2 Ry2 即 R R z 某些线性组合中某些零点与极点相抵消,则收敛域可能扩 大。 (表现为叠加性和均匀性)

二.位移性 1.双边z变换 2.单边z变换 山)左移位性质 2)右移位性质
X 第 4 二.位移性 页 1.双边z变换 2.单边z变换 (1) 左移位性质 (2) 右移位性质
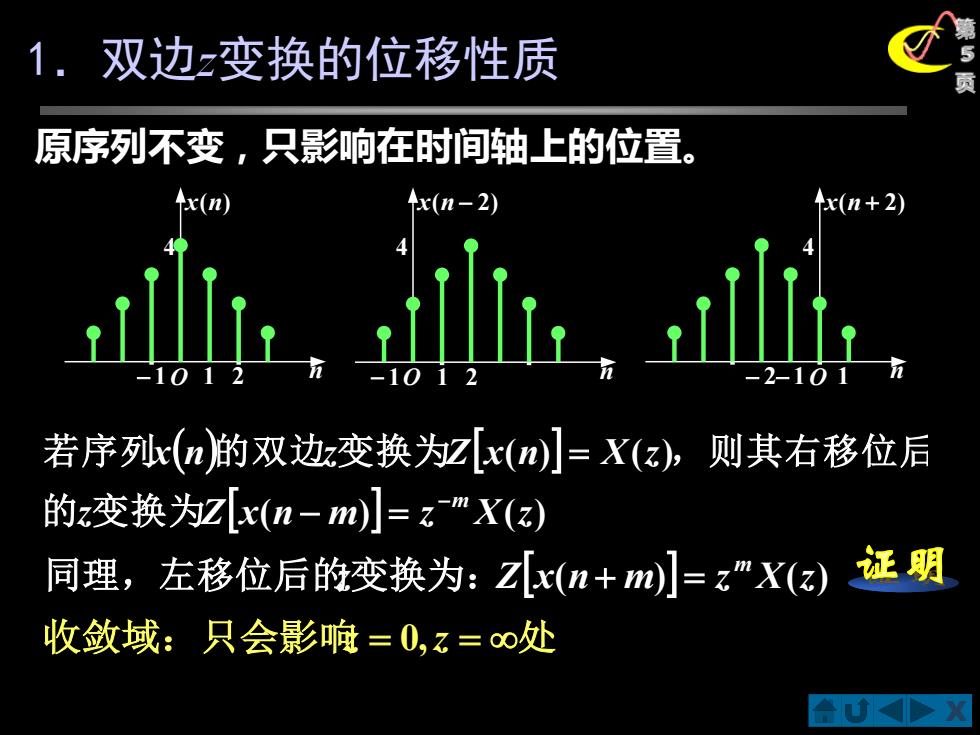
1.双边z变换的位移性质 原序列不变,只影响在时间轴上的位置。 Ax(n) x(n-2) x(n+2) 2-101 若序r(n)的双边z变换为z[x(m]=X(a),则其右移位后 的z变换为z[x(n-m)=zmX(a) 同理,左移位后的变换为:Z(n+m]=z"X(a)证明 收敛域:只会影响=0,z=∞处 合UD
X 第 5 页 O n x(n) 4 O n x(n − 2) 4 O n x(n + 2) 4 − 1 1 2 − 1 1 2 − 2− 1 1 原序列不变,只影响在时间轴上的位置。 收敛域:只会影响z = 0,z = 处 ( ) ( ) ( ) ( ) ( ) z Z x n m z X z x n z Z x n X z −m − = = 的 变换为 若序列 的双边 变换为 ,则其右移位后 1.双边z变换的位移性质 z Zx(n m) z X(z) m 同理,左移位后的变换为: + =