
飞号与事空 §72离散时间信号—序列 离散信号的表示方法 •离散时间信号的运算 常用离散时间信号 新疆大学信息科学与工程学院电子系 2003.1 退出 开始
新疆大学信息科学与工程学院电子系 2003.1 §7.2 离散时间信号——序列 •离散信号的表示方法 •离散时间信号的运算 •常用离散时间信号
离散信号的表示方法 x(d)→x(nT)等间隔Tx(n) n=0,±1,±2,. 数字序列如{.0.9,0.8,0.3,0.1 侧题 有规则的可以用函数表示x(n) 波形表示:线段的长短表示各序列值的大小 {x(n}与x(n)概念上有区别,但为了书写方便,常以x(n) 表示整个序列,在应用场合一般不会混淆
X 第 2 一.离散信号的表示方法 页 ( ) = 波形表示 线段的长短表示各序列值的大小 有规则的可以用函数表示 数字序列 如 : , : 0.9,0.8,0.3,0.1 0 x n n ( ) ( ) ( ) 表示整个序列,在应 用场合一般不会混淆 。 与 概念上有区别,但为了书写方便,常以 x n x n x n x(t)→ x(nT) 等间隔T x(n) n = 0,1,2,
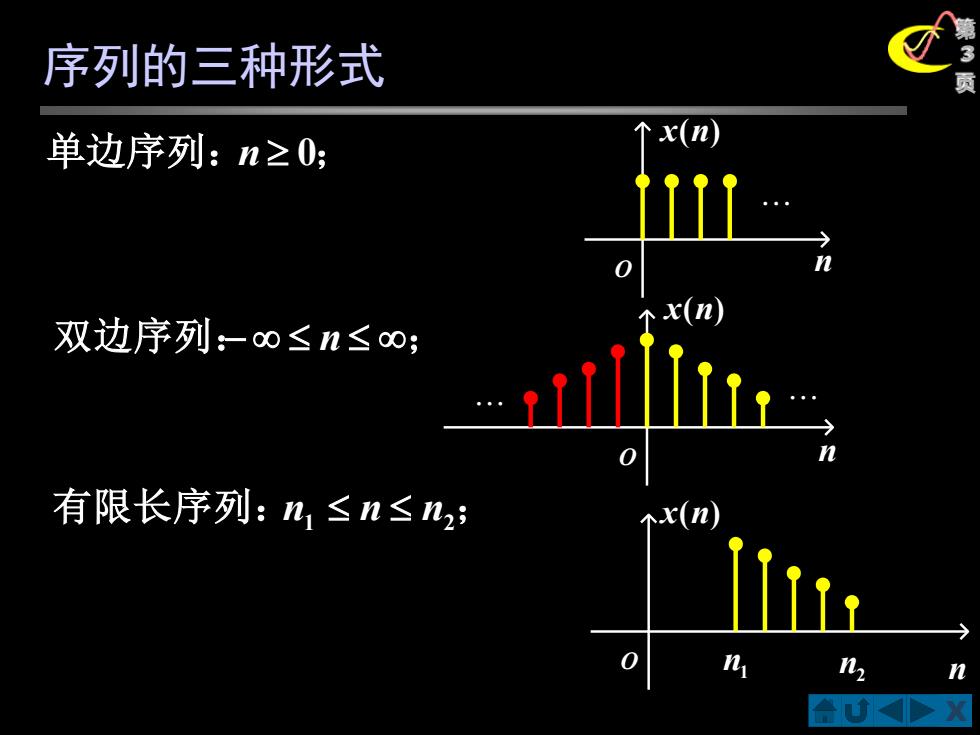
序列的三种形式 单边序列:n≥0; 个x(n) 0 个x(n) 双边序列:-o≤n≤o; 有限长序列:n1≤n≤n2; c(n n n
X 第 3 序列的三种形式 页 O x(n) n O x(n) n O x(n) n1 n2 n 双边序列:− n ; 单边序列:n 0; 有限长序列:n1 n n2 ;

离散信号的运算 1.相加: (n)=x(n)+y(n) 2.相乘:z(m)=x(nm)yn) 3.乘系数:(m)=r(n) 4.移位:z(n)=x(n-m) 右移位 z(n)=x(n+m) 左移位 4x(n) (n-) x(0) p(0) x(-1) x(1) x(3 x(1) -10 2 (2 2 合UDN
X 第 4 二.离散信号的运算 页 1.相加: 2.相乘: 3.乘系数: z(n) = x(n) + y(n) z(n) = x(n) y(n) z(n) = ax(n) 左移位 右移位 ( ) ( ) ( ) ( ) z n x n m z n x n m = + 4.移位: = − o n x(n −1) 1 2 3 x(− 1) x(0) x(1) x(3) x(2) o n − 1 4 x(n) 1 2 3 x(−1) x(0) x(1) x(3) x(2) − 1

5.倒置:()=x(-) 6. 差分:前向差分:△x(m=x(n+1)-x(n) 后向差分:Vx(m)=x(n)-x(n-1) 7.累加:z(m=∑x() 8.重排(压缩、扩展) 0nR0→8 倒题 注意:有时需去除某些点或补足相应的零值。 9.序列的能量E=∑x(m 1=-co
X 第 5 页 z(n) = x(−n) ( ) ( ) ( 1) ( ) ( 1) ( ) = − − = + − x n x n x n x n x n x n 后向差分: 前向差分: =− = k z(n) x(k) 5.倒置: 6.差分: 7.累加: 8.重排(压缩、扩展): ( ) ( ) ( ) → → a n x n x an ,或 x n x 注意:有时需去除某些点或补足相应的零值。 9.序列的能量 =− = n n E x n 2 ( )