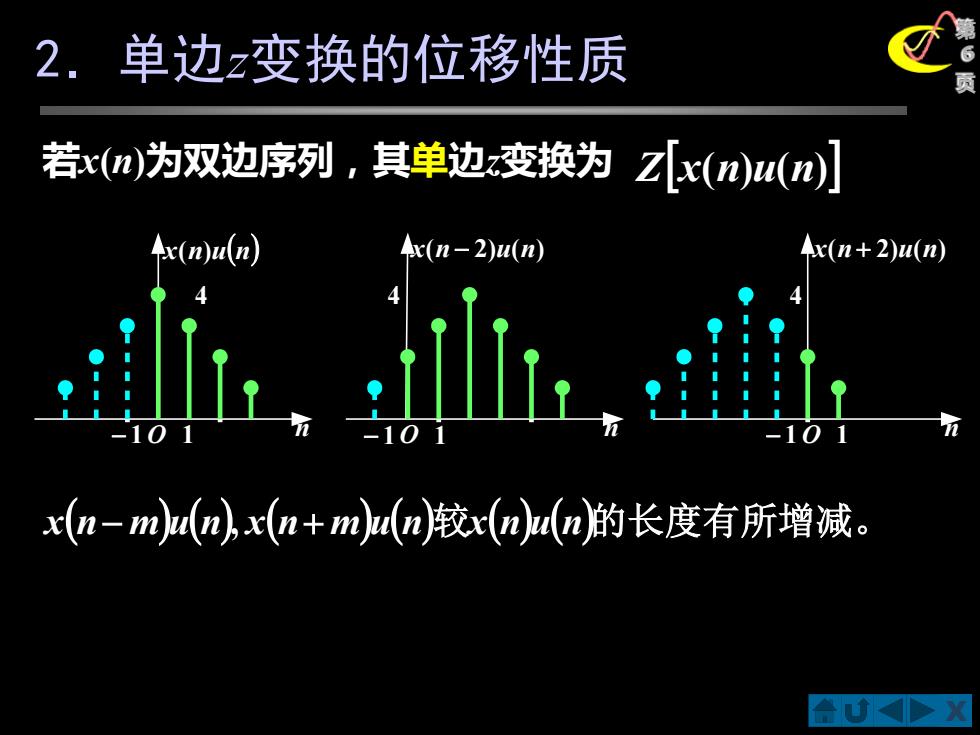
2.单边z变换的位移性质 若xm为双边序列,其单边变换为Zx(m)u(n] x(n)u(n) x(n-2)w(n) x(n+2)u(n x(n-md(n,x(n+m)a(n较x(nu(n的长度有所增减
X 第 6 2.单边 页 z变换的位移性质 O n x(n)u(n) 4 n x(n − 2)u(n) 4 n x(n + 2)u(n) 4 − 1 1 − 1 O 1 − 1 O 1 x(n− m)u(n), x(n+ m)u(n)较x(n)u(n)的长度有所增减。 若x(n)为双边序列,其单边z变换为 Zx(n)u(n)

(1)左移位性质 若Zx(n)u(m=X(a 则n+mwj-:rxa- 其中m为正整数 证明 z(n+1]=xX()-) Zx(n+2=z2X)-z2x0)-2x
X 第 7 页 (1)左移位性质 若 Zx(n)u(n)= X(z) + = − − = − 1 0 ( ) ( ) ( ) ( ) m k m k 则 Z x n m u n z X z x k z 其中m为正整数 Zx(n + 1) = zX(z)− zx(0) ( 2) ( ) (0) (1) 2 2 Z x n+ = z X z − z x − zx