
介质极化 ,在各向同性的电介质中,某点处的分子平均偶极矩与该处 的外电场强度成正比,而在很小的体积元内,可看作是均 匀的,故电极化强度矢量也与该处的电场强度成正比,可 表示为: P(F)=EoxE ,其中X。称为介质的电极化率,是一个无量纲的常数。 Note:若介质是非各向同性,则p与电场方向不一致, pE不成立,故p与E不同向; 12 lexu@mail.xidian.edu.cr
在各向同性的电介质中,某点处的分子平均偶极矩与该处 的外电场强度成正比,而在很小的体积元内,可看作是均 匀的,故电极化强度矢量也与该处的电场强度成正比,可 表示为: 其中 称为介质的电极化率,是一个无量纲的常数。 Note:若介质是非各向同性,则 与电场方向不一致, 不成立,故 与 不同向; 12 lexu@mail.xidian.edu.cn ( ) eExrP 0 = ε p Ep ∝ p E e x XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

束缚电荷 ,介质极化后,其内部电荷的重新排列, 出现沿电场方向的一系列等效电偶极子。 若外电场和介质都是均匀的,则电偶极 )∈D 子排列的结果使得介质内部正负电荷相 互抵消,在介质表面出现一层面电荷。 若介质或外加电场不均匀,则介质内部 出现体电荷,这些电荷被紧紧地束缚在 分子内,不能自由移动,称为束缚电荷 外电场E ,束缚电荷在空间激发电场,介质中的总电场是外加电场与 束缚电荷产生的场之和,因此,介质中的电场不同于真空 中的电场。 13 lexu@mail.xidian.edu.cn
介质极化后,其内部电荷的重新排列, 出现沿电场方向的一系列等效电偶极子。 ◦ 若外电场和介质都是均匀的,则电偶极 子排列的结果使得介质内部正负电荷相 互抵消,在介质表面出现一层面电荷。 ◦ 若介质或外加电场不均匀,则介质内部 出现体电荷,这些电荷被紧紧地束缚在 分子内,不能自由移动,称为束缚电荷。 束缚电荷在空间激发电场,介质中的总电场是外加电场与 束缚电荷产生的场之和,因此,介质中的电场不同于真空 中的电场。 13 lexu@mail.xidian.edu.cn XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

束缚电荷 设极化介质的体积为V,表面积是S,极化强度是P,现在 计算介质外部任一点的电位。 ,在介质中r'处取一个体积元△V',因r-远大于△V'的线 度,故可将△V'中介质当成一偶极子,其偶极矩为 △p=P△V',它在r处产生的电位是 dy' Ao(r)= P(r△V'F-F 4π8。|F-F 则V'内所有电偶极子产生的电位为:S .dv F-F 14 lexu@mail.xidian.edu.cn
设极化介质的体积为V,表面积是S,极化强度是P,现在 计算介质外部任一点的电位。 在介质中r′处取一个体积元ΔV′, 因|r-r′|远大于ΔV′的线 度,故可将ΔV′中介质当成一偶极子,其偶极矩为 Δp=PΔV′,它在r处产生的电位是 则V’内所有电偶极子产生的电位为: 14 lexu@mail.xidian.edu.cn 3 0 ( ') ' ' ( ) 4 ' Pr V r r r r r ϕ πε ∆ − ∆= ⋅ − 3 0 1 ( ') ( ') ( ) ' 4 ' V Pr r r r dV r r ϕ πε ⋅ − = ⋅ − ∫ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

束缚电荷 利用V F-列 F-- 。V'表示对源点坐标的微分运算,而V表示对场点坐标的 微分运算. 0= 4πG0 V.(ua)=Vu.A+uv.A S是包围 体积V表面, PVE-E-V. -厂 n是S的 外法线 I'ds V.P 单位矢量。 P.n ds'+ dv' 460 πE。JF-F 15 lexu@mail.xidian.edu.cn
◦ ▽’表示对源点坐标的微分运算,而▽表示对场点坐标的 微分运算. 15 lexu@mail.xidian.edu.cn 3 1 1 r r rr rr r r − ′ ∇ = −∇ = − ′ − − ′ ′ − ′ 利用 ∫ ′ − ′ = ⋅∇′ V Vd rr P 1 4 1 πε 0 φ ( ) AuAuAu ⋅∇+⋅∇=⋅∇ P rrrr P rr P ′ ⋅∇ − ′ − − ′ = ′ ⋅∇ − ′ ⋅∇′ 1 1 ( ) 0 0 0 0 1 1 4 4 1 1 4 4 S V S V P P dS dV r r r r P n P dS dV r r r r φ πε πε πε πε ∇ ⋅′ = ⋅−′ ′ − − ′ ′ −∇ ⋅′ ⋅ = ′ ′ + − − ′ ′ ∫ ∫ ∫ ∫ S是包围 体积V表面, 是S的 外法线 单位矢量。 n XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
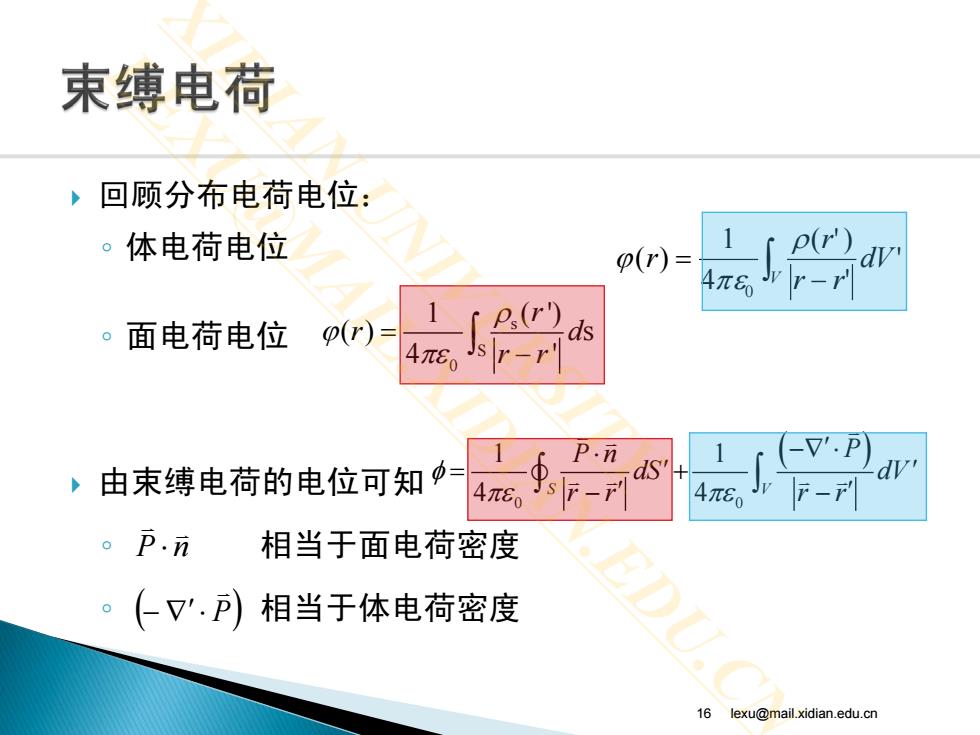
束缚电荷 回顾分布电荷电位: 。体电荷电位 p(r)= p(r)dv 4π6Fr-r 。面电荷电位 p(r)= 1 P(r) ds Js r-r P.n -V'P) ,由束缚电荷的电位可知 ds' 1 4π.sF-F 4π。JrF- 。P.n 相当于面电荷密度 (V'.P)相当于体电荷密度 16 lexu@mail.xidian.edu.cn
回顾分布电荷电位: ◦ 体电荷电位 ◦ 面电荷电位 由束缚电荷的电位可知 ◦ 相当于面电荷密度 ◦ 相当于体电荷密度 16 lexu@mail.xidian.edu.cn ( ) 0 0 1 1 4 4 S V P n P dS dV r r r r φ πε πε −∇ ⋅′ ⋅ = ′ ′ + − − ′ ′ ∫ ∫ ∫ − = V dV rr r r ' ' )'( 4 1 )( 0 ρ πε ϕ s S 0 1 ( ') ( ) s 4 ' r r d r r ρ ϕ πε = − ∫ nP ⋅ ( ) P − ′ ⋅∇ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN