
结果分析 参数 参数估计值 置信区间 B。 17.3244 |5.728228.9206 B 1.3070 [0.68291.93111 B2 -3.6956 -7.4989 0.1077] F 0.3486 0.0379 0.65941 R2=0.9054 F=82.9409 p=0.0000 的90.549%可由模型确定 F远超过检验的临界值 匹小于o=0.05 模型从整体上看成立 B,的置信区间包含零点 x,对因变量的 右端点距零点很近 影响不太显著 x,2项显著 可将x,保留在模型中 教学建摸 00
结果分析 y的90.54%可由模型确定 参数 参数估计值 置信区间 17.3244 [5.7282 28.9206] 1.3070 [0.6829 1.9311 ] -3.6956 [-7.4989 0.1077 ] 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 0 1 2 3 = + + + + 2 0 1 1 2 2 3 2 y x x x F远超过F检验的临界值 p远小于=0.05 2的置信区间包含零点 (右端点距零点很近) x2对因变量y 的 影响不太显著 x2 2项显著 可将x2保留在模型中 模型从整体上看成立

1 销售量预测 且,中中名+0 价格差x,=其它厂家价格x本公司价格x 调整x 空制 围过,锁训 控制价格差x,=0.2元,投入广告费x,=650万元 )=B,+Bx+Bx+月x污=8.2933 百万支) 销售量预测区间为7.8230,8.7636](置信度95%) 上限用作库存管理的目标值下限用来把握公司的现金流 若估计x3=3.9,设定x4=3.7,,则可以95%的把握 知道销售额在7.8320x3.7≈29(百万元)以上 数学建摸
2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ 销售量预测 y ˆ = + x + x + x 价格差x1 =其它厂家价格x3 -本公司价格x4 估计x3 调整x4 控制价格差x1 =0.2元,投入广告费x2 =650万元 销售量预测区间为 [7.8230,8.7636](置信度95%) 上限用作库存管理的目标值 下限用来把握公司的现金流 若估计x3 =3.9,设定x4 =3.7,则可以95%的把握 知道销售额在 7.83203.7 29(百万元)以上 控制x1 通过x1 , x2预测y 8.2933 ˆ ˆ ˆ ˆ ˆ 2 y = 0 + 1 x1 + 2 x2 + 3 x2 = (百万支)
模型改进 y= P。+Bx1+B2x2+Bx3 +8 和x,对 参数 参数估计值 置信区间 的影响独立 17.3244 [5.728228.92061 B 1.3070 0.6829 1.9311 B2 -3.6956 -7.4989 0.10771 x,和x对 0.3486 0.03790.65941 的影响有 R2=0.9054 F=82.9409 p=0.0000 交互作用 y=B+Bx+B2x2+B:x2+Bax x2+ 参数 参数估计值 置信区间 29.1133 [13.701344.5252 B 11.1342 1.977820.29061 -7.6080 L-12.6932-2.52281 0.6712 I0.25381.08871 B -1,4777 -2.8518-0.10371 R2=0.9209 F=72.7771 教学建模 p0.06
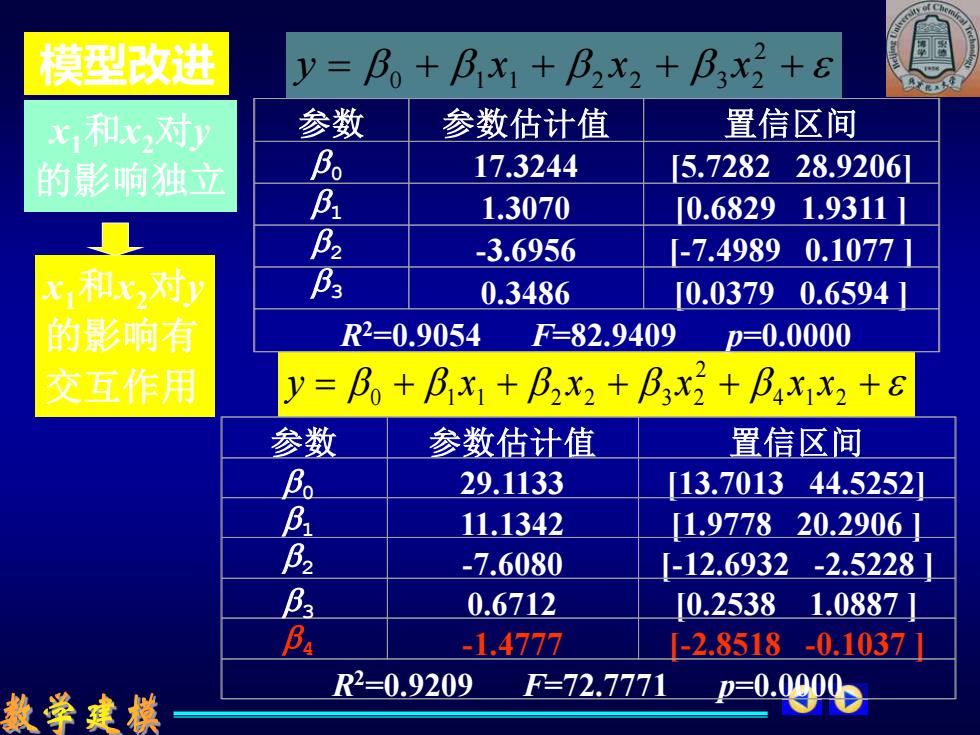
模型改进 x1和x2对y 的影响独立 = + + + + 2 0 1 1 2 2 3 2 y x x x = + + + + + 4 1 2 2 0 1 1 2 2 3 2 y x x x x x 参数 参数估计值 置信区间 17.3244 [5.7282 28.9206] 1.3070 [0.6829 1.9311 ] -3.6956 [-7.4989 0.1077 ] 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 0 1 2 3 参数 参数估计值 置信区间 29.1133 [13.7013 44.5252] 11.1342 [1.9778 20.2906 ] -7.6080 [-12.6932 -2.5228 ] 0.6712 [0.2538 1.0887 ] -1.4777 [-2.8518 -0.1037 ] R2=0.9209 F=72.7771 p=0.0000 3 0 1 2 4 x1和x2对y 的影响有 交互作用

两模型销售量预测比较 控制价格差x,=0.2元,投入广告费x2=6.5百万元 )= 8.2933 百万支 )=月。+Bx+Bx2+Bx号 ☒间7.8230,8.7636 )=8.3272(百万支 =B+Bx+B2x2+阝x3+Bxx2 间17.8953,8.7592 略有增加 预测区间长度更短 数学建摸
两模型销售量预测比较 4 1 2 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x + x x 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x y ˆ = 8.2933 (百万支) 区间 [7.8230,8.7636] 区间 [7.8953,8.7592] y ˆ = 8.3272 (百万支) 控制价格差x1 =0.2元,投入广告费x2 =6.5百万元 y ˆ 略有增加 预测区间长度更短

两模型少与心,关系的比较 了=中有t+xs+民中+B 9 9 8.5 8.5 x=6.5 8 8 7.5 0.2 7.5 0.2 0.4 0.6 .2 0 0.2 0.40.6 o 10.5 9.5 10 x1=0.2 9.5 8.5 9 8 8.5 7.5 8 6 个 2 5 6 8
x2 =6.5 x1 =0.2 -0.2 0 0.2 0.4 0.6 7.5 8 8.5 9 x1 y ˆ -0.2 0 0.2 0.4 0.6 7.5 8 8.5 9 x1 y ˆ 5 6 7 8 7.5 8 8.5 9 9.5 10 x2 y ˆ 5 6 7 8 8 8.5 9 9.5 10 10.5 x2 y ˆ 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x 4 1 2 2 0 1 1 2 2 3 2 ˆ ˆ ˆ ˆ y ˆ = + x + x + x + x x 两模型 与x1 y ˆ ,x2关系的比较