
西安电子科技大学离散数学软件学院第二篇集合论第4章函数与无限集合第21课时4.1函数的概念?第22课时4.2逆函数和复合函数第23课时4.3可数与不可数集合第24课时4.4集合基数的比较
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第21课时 4.1 函数的概念 第4章 函数与无限集合 4.3 可数与不可数集合 4.2 逆函数和复合函数 4.4 集合基数的比较 第22课时 第23课时 第24课时

西安电子科技大学函数的定义$4.1.1软件学院家家家设X和Y是集合,是从X到Y上的二元关系,函数如果对于每一个xEX都有唯一的yEY,使得<x,y>Ef,称为从X到Y的函数,记为:X一Y。函数又称作映射或变换。函数的形式定义J :X-Y(Vx)(xEX-(Fy)(yEYA<X, yPE f A(YZ)(ZEA<X,Z>E J -y-z)函数区别于一般二元关系的两个特点:(1)函数的定义域等于前域:(2)对于前域每个元素,陪域中仅有唯一的一个象与之对应
西安电子科技大学 函数的定义 软件学院 函数 §4.1.1 函数的形式定义 函数区别于一般二元关系的两个特点: (1)函数的定义域等于前域; (2)对于前域每个元素,陪域中仅有唯一的一个象与之对应
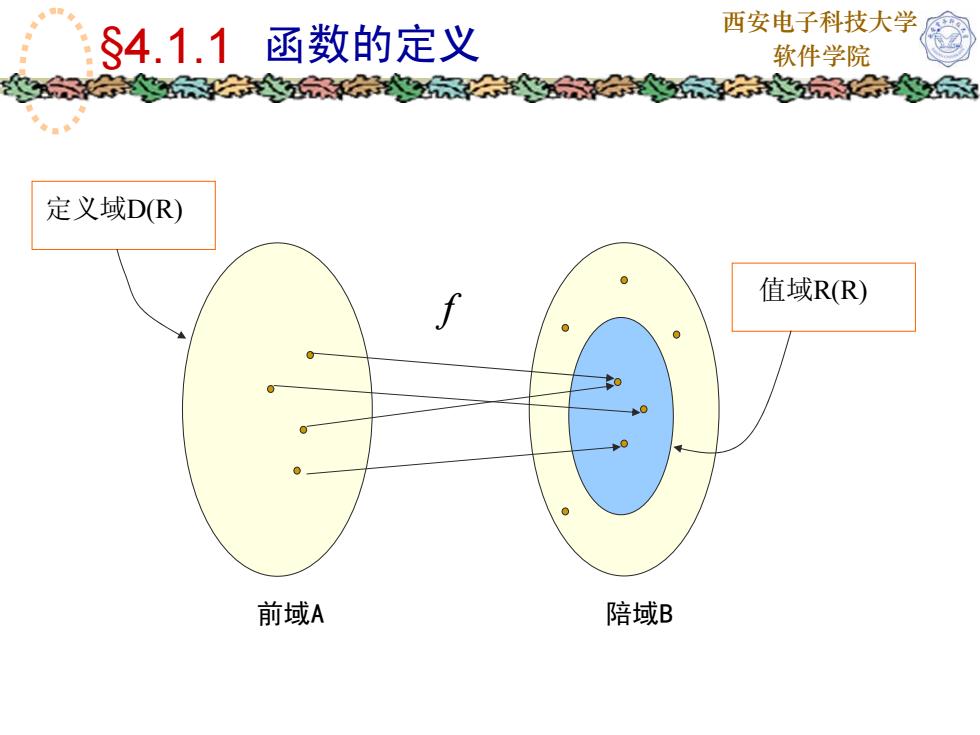
西安电子科技大学函数的定义$4.1.1软件学院定义域D(R)值域R(R)前域A陪域B
西安电子科技大学 软件学院 值域R(R) 定义域D(R) 前域A 陪域B §4.1.1 函数的定义 f

西安电子科技大学函数的定义$5.1.1软件学院家家设为从集合X到Y的函数,任取xEX,象若<x,y>Ef,则称y为在f作用下x的映象(简称象),记为f(x)=y,而x则称为y的原象。若XCX,称f(X)=f(x)IXEX为函数f下X的映象。特别地,称整个前域的映象f(X)为函数的值域
西安电子科技大学 函数的定义 软件学院 象 §5.1.1

西安电子科技大学函数的定义$4.1.1软件学院(例题)判断下列关系中哪些能构成函数(a) =(<X1,X2>x1,X2EN,XI+x2<10)(b) =(<y1, y2>/y1, y2ER,y2=y1)(c)=(<1,82>X1X2EN,x2为小于x1的素数个数)解答:(a)不能,因为D()N,且每个1对应多个。(b)不能,一个y1对应多个y2.(c)能。因为D(f)=N,且对每个x1EN,都有唯一的元素x2EN与之对应
西安电子科技大学 §4.1.1 函数的定义 软件学院 【例题】判断下列关系中哪些能构成函数 解答: