
西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时V3.1集合及其运算第14课时3.2二元关系→第15课时3.3集合上的二元关系及其特性第16课时3.4关系的闭包运算3.5等价关系第17-18课时第19-20课时3.6序关系
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-18课时 第15课时 3.3 集合上的二元关系及其特性 第19-20课时 3.6 序关系

西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院茶家家两个元素a和b组成的具有固定次序的序列,序偶记为<a,b>。例如:<北京,上海>表示某火车行驶的起点和终点。《<北京,上海>≠<上海,北京>两个序偶<a1,b,>=<a2,b2>的充要条件是:ai=a2且bi=b2
西安电子科技大学 两个集合的笛卡儿积 软件学院 序偶 §3.2.1 两个元素a和b组成的具有固定次序的序列, 记为<a, b> 。 两个序偶<a 1 , b 1 >=<a 2 ,b 2 >的充要条件是: a 1 =a 2 且b 1 =b 2 例如:<北京,上海> 表示某火车行驶的起点和终点。 <北京,上海>≠<上海,北京>

西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院家笛卡儿积设A和B是两个集合,称集合AxB={<a,b>aEA^bEB为集合A和B的笛卡儿积或叉集
西安电子科技大学 软件学院 笛卡儿积 §3.2.1 两个集合的笛卡儿积 设A和B是两个集合,称集合 为集合A和B的笛卡儿积或叉集。 × = < >|,{ ∈ ∧ ∈ BbAabaBA }

西安电子科技大学S3.2.1两个集合的笛卡儿积软件学院茶家【例题】设A=a,b),B={a,β),求AXB解答:AxB={<a, α >,<a, β>,<b, α >,<b, β>}
西安电子科技大学 软件学院 【例题】设A={a, b}, B={α, β},求A×B §3.2.1 两个集合的笛卡儿积 解答: A×B={<a, α >,<a, β >,<b, α >,<b, β >}
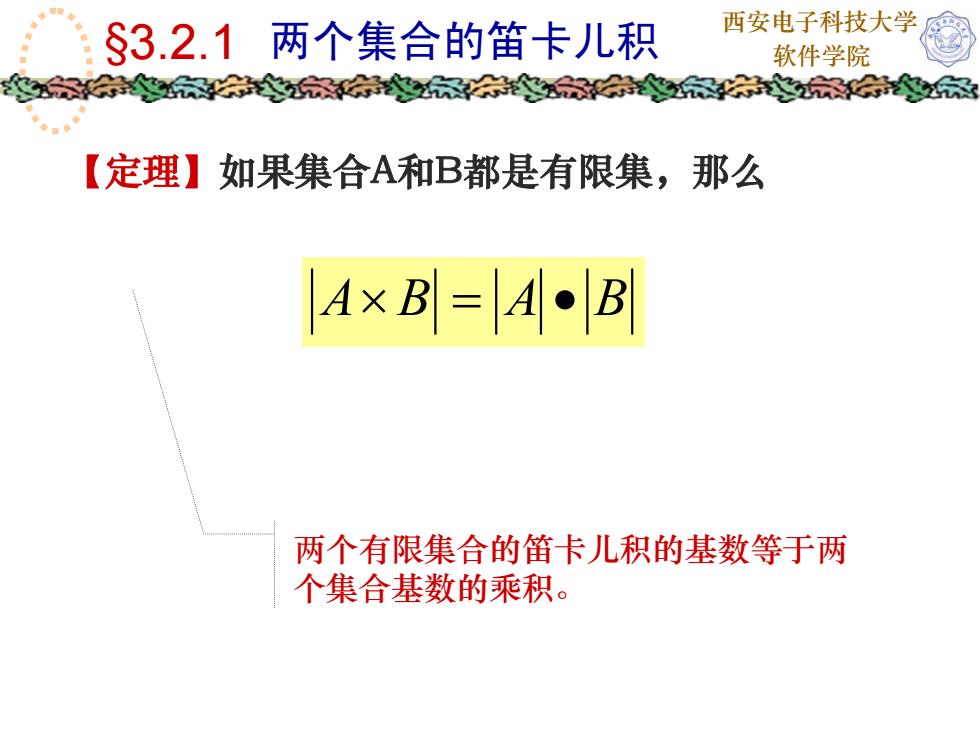
西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院家家【定理】如果集合A和B都是有限集,那么A×B=|A·|Bl两个有限集合的笛卡儿积的基数等于两个集合基数的乘积
西安电子科技大学 §3.2.1 两个集合的笛卡儿积 软件学院 【定理】如果集合A和B都是有限集,那么 •=× BABA 两个有限集合的笛卡儿积的基数等于两 个集合基数的乘积