西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时V3.1集合及其运算第14课时3.2二元关系X第15课时3.3集合上的二元关系及其特性→第16课时3.4关系的闭包运算第17课时3.5等价关系(1)第19-20课时3.6序关系A
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 (1) 第14课时 第16课时 第17课时 第15课时 3.3 集合上的二元关系及其特性 第19-20课时 3.6 序关系
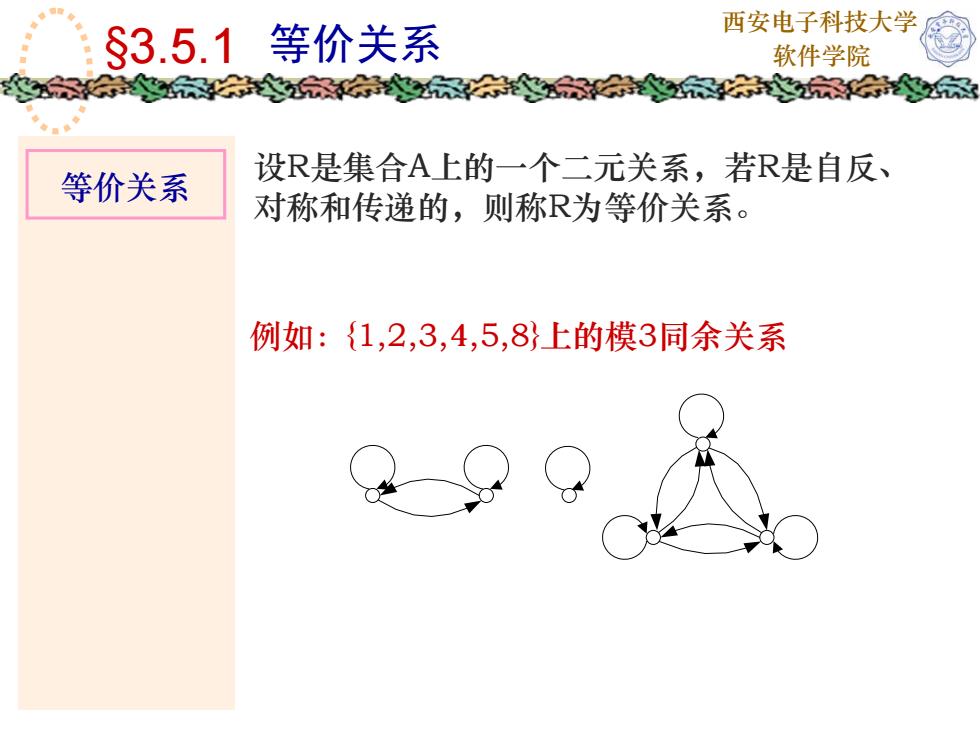
西安电子科技大学等价关系$3.5.1软件学院家家设R是集合A上的一个二元关系,若R是自反等价关系对称和传递的,则称R为等价关系。例如:1,2,3,4,5,8上的模3同余关系
西安电子科技大学 §3.5.1 等价关系 软件学院 等价关系 设R是集合A上的一个二元关系,若R是自反、 对称和传递的,则称R为等价关系。 例如:{1,2,3,4,5,8}上的模3同余关系

西安电子科技大学等价关系$3.5.1软件学院等价关系的关系图的特点:所有结点上自反性有自回路只要结点r到s可达正对称与传递性则r到s有边相连等价关系的关系图的每个连通子图都是有向完全图
西安电子科技大学 软件学院 等价关系的关系图的每个连通子图 都是有向完全图 。 自反性 对称与传递性 所有结点上 有自回路 只要结点r到s可达 则r到s有边相连 等价关系的关系图的特点: §3.5.1 等价关系

西安电子科技大学S3.5.1等价关系软件学院家【例题】A=(a,b,,d),A上的二元关系R=(<a,a>,<a,b><b,a>,<b, b>,<c, c>,<c,d>,<d,c>,<d,d>),验证关系R是等价关系。解答:(i)因为I二R,所以是自反的:(ii) 因为R-1={<a, a>,<b,a>,<a, b>,<b, b>,<c,c>,<d,c>,<c,d>,<d,d>)=R,所以R是对称的;(ii) 因为R.R={<a, b>,<a, a>,<b, a>,<b,b>,<c,d>,<C,c>,<d,d>,<d,c>}二R,所以R是传递的。综上所述,R是等价关系,其关系图如图所示
西安电子科技大学 软件学院 【例题】A={a, b, c, d},A上的二元关系R={<a, a>, <a, b>, <b, a>, <b, b>, <c, c>, <c, d>, <d, c>, <d, d>},验证关 系R是等价关系。 §3.5.1 等价关系 解答: (i)因为IA⊆R,所以是自反的; (ii)因为R-1={<a, a>, <b, a>, <a, b>, <b, b>, <c, c>, <d, c>, <c, d>, <d, d>}= R,所以R是对称的; (iii)因为R◦R={<a, b>, <a, a>, <b, a>, <b, b>, <c, d>, <c, c>, <d, d>, <d, c>}⊆R,所以R是传递的。 综上所述,R是等价关系,其关系图如图所示

西安电子科技大学等价关系$3.5.1软件学院【例题】设I为整数集,I上的模3相等关系R={<x,y>]x三y(mod3,证明R是等价关系。证明:(i)对于任一aEI,有a三a(mod 3),即<a,a>ER,所以R是自反的;(ii)若<a,b>ER,则有a=b(mod3),即存在mEI,使得a-b=3m,于是有b-a=-3m,因此b=a(mod3),即<b,a>ER,所以R是对称的。(iii)若<a,b>,<b,c>ER,则有a=b(mod3)和b=o(mod3),即存在m,nEI,使得a-b=3m和b-c=3n,将等式两边相加得a-c=3(m+n)因此a三c(mod 3),即<a,c>ER,所以R是传递的。综上所述,R是等价关系
西安电子科技大学 §3.5.1 等价关系 软件学院 【例题】设I为整数集,I上的模3相等关系R={<x, y>| x≡y(mod 3)},证明R是等价关系。 证明: (i)对于任一a∈I,有a≡a (mod 3),即<a, a>∈R,所 以R是自反的; (ii)若<a, b>∈R,则有a≡b (mod 3),即存在m∈I, 使得a-b=3m,于是有b-a=-3m,因此b≡a (mod 3),即<b, a>∈R,所以R是对称的。 (iii)若<a, b>,<b, c>∈R,则有a≡b (mod 3)和b≡c (mod 3),即存在m,n∈I,使得a-b=3m和b-c= 3n,将等 式两边相加得a-c=3( m+n) 因此a≡c (mod 3),即<a, c>∈R,所以R是传递的。 综上所述,R是等价关系