
西安电子科技大学离散数学软件学院家第四篇图论第6章图论第27-28课时6.1图的基本概念(1)第29课时6.2路径与回路A第30课时6.3图的矩阵表示第32课时6.4欧拉图与汉密尔顿图(2)A第33课时6.5平面图第34课时6.6图的着色6.7 树第35-36课时第37-38课时6.8图的应用
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念(1) 第6章 图论 6.4 欧拉图与汉密尔顿图(2) 6.2 路径与回路 6.5 平面图 第29课时 第33课时 第30课时 6.3 图的矩阵表示 第34课时 6.6 图的着色 第32课时 第35-36课时 6.7 树 第27-28课时 第37-38课时 6.8 图的应用
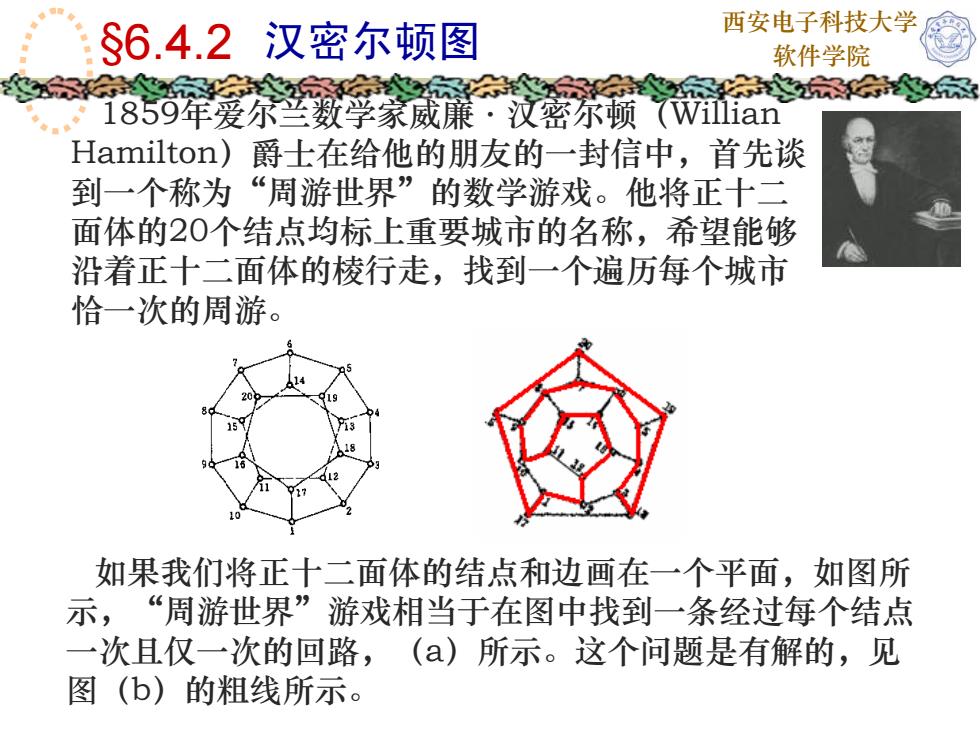
西安电子科技大学$6.4.2汉密尔顿图软件学院1859年爱尔兰数学家威廉·汉密尔顿(WillianHamilton)爵士在给他的朋友的一封信中,首先谈到一个称为“周游世界”的数学游戏。他将正十二面体的20个结点均标上重要城市的名称,希望能够沿着正十二面体的棱行走,找到一个遍历每个城市恰一次的周游。如果我们将正十二面体的结点和边画在一个平面,如图所示,“周游世界”游戏相当于在图中找到一条经过每个结点一次且仅一次的回路,(a)所示。这个问题是有解的,见图(b)的粗线所示
西安电子科技大学 §6.4.2 汉密尔顿图 软件学院 1859年爱尔兰数学家威廉·汉密尔顿(Willian Hamilton)爵士在给他的朋友的一封信中,首先谈 到一个称为“周游世界”的数学游戏。他将正十二 面体的20个结点均标上重要城市的名称,希望能够 沿着正十二面体的棱行走,找到一个遍历每个城市 恰一次的周游。 如果我们将正十二面体的结点和边画在一个平面,如图所 示,“周游世界”游戏相当于在图中找到一条经过每个结点 一次且仅一次的回路,(a)所示。这个问题是有解的,见 图(b)的粗线所示

西安电子科技大学$6.4.2汉密尔顿图软件学院经过图G-<V,E>中的每个结点一次且仅一次的路径。汉密尔顿路径汉密尔顿回路经过图G-<V,E>中的每个结点一次且仅一次的回路。汉密尔顿图含哈密尔顿回路的图
西安电子科技大学 软件学院 汉密尔顿路径 §6.4.2 汉密尔顿回路 汉密尔顿图 汉密尔顿图
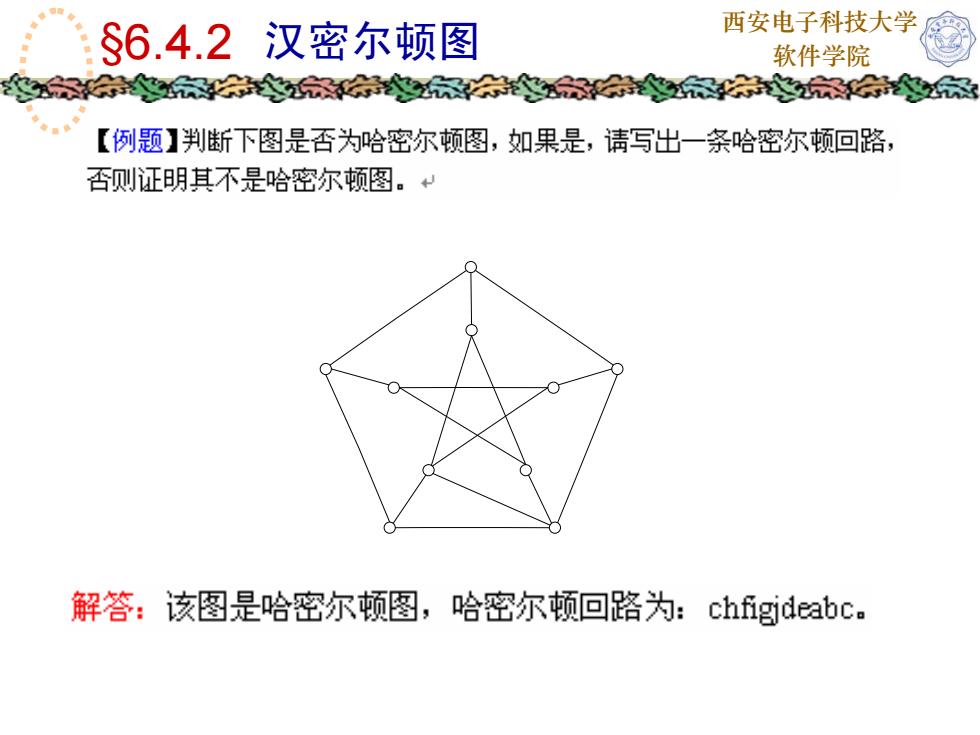
西安电子科技大学$6.4.2汉密尔顿图软件学院家【例题1判断下图是否为哈密尔顿图,如果是,请写出一条哈密尔顿回路否则证明其不是哈密尔顿图。+解答:该图是哈密尔顿图,哈密尔顿回路为:chfigideabc
西安电子科技大学 §6.4.2 汉密尔顿图 软件学院
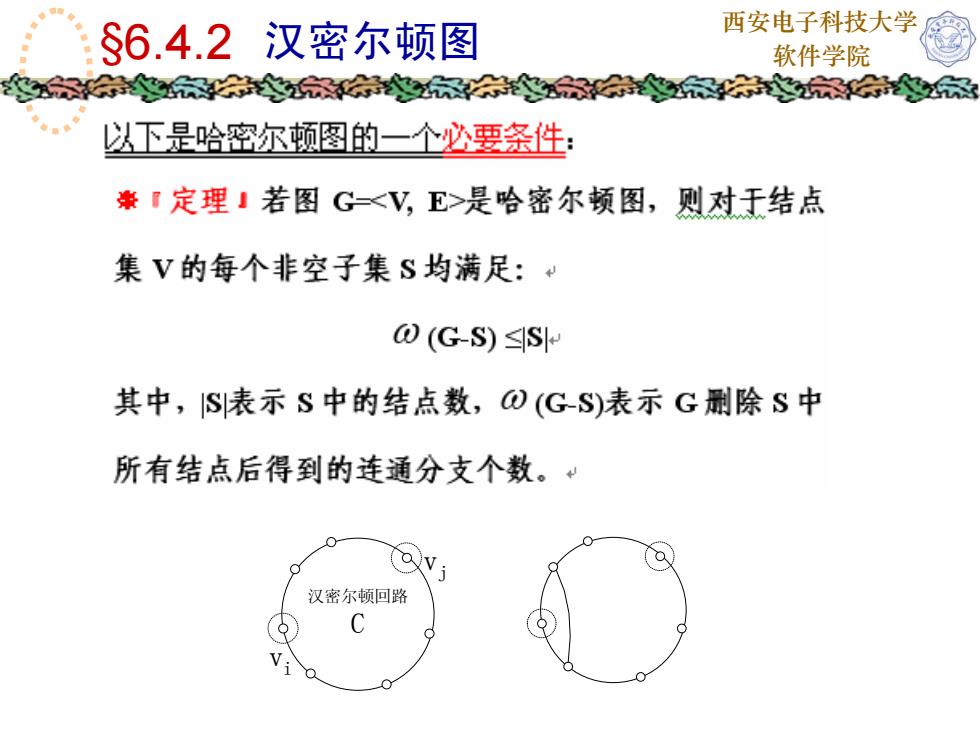
西安电子科技大学S6.4.2汉密尔顿图软件学院以下是哈密尔顿图的一个必要条件案定理」若图G-<V,E>是哈密尔顿图,则对于结点集V的每个非空子集S均满足:U (G-S) ≤S其中,IS表示S中的结点数,①(G-S)表示G删除S中所有结点后得到的连通分支个数。汉密尔顿回路
西安电子科技大学 软件学院 汉密尔顿回路 C vi vj §6.4.2 汉密尔顿图