
西安电子科技大学离散数学软件学院第一篇数理逻辑第2章谓词逻辑V第7课时1.1谓词和量词第8课时1.2谓词公式→第9课时1.3谓词公式的翻译41第10课时1.4谓词演算的永真公式第11课时1.5谓词演算的四个推理规则第12课时1.6谓词逻辑推理及应用二
西安电子科技大学 离散数学 软件学院 第一篇 数理逻辑 第7课时 1.1 谓词和量词 第2章 谓词逻辑 1.4 谓词演算的永真公式 1.2 谓词公式 1.5 谓词演算的四个推理规则 第8课时 第10课时 第11课时 第9课时 1.3 谓词公式的翻译 第12课时 1.6 谓词逻辑推理及应用

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院家家家【例题】符号化以下语句,并推证结论的有效性,“每个人都是要死的,苏格拉底是人,所以苏格拉底是要死的。解答:设论域为全总个体域,M(x):x是人,D(x):x是要死的,a:苏格拉底。现要证明以下永真式:(x)(M(x)-D(x) AM(a)→D(a)P(1) M(a)P(2) (Vx(M(x)-D(x)(3) M(a)D(a)T (2) US(4) D(a)T(1)(3)I
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院
西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院【例题 证明(x)(C(×)→W(×) ΛR(x)), (日x)(C(x) ΛQ()), (日x)(Q(≤) ^R(x))P(1) (日x)(C(×) ^Q(×)(2)C(c) Λ Q(c)T (1) ES(3)Q(c)T (2) I(4)C(c)T (2) IP(5)(V x)(C(×)-→W(×) ^R(×)(6)C(c)-W(c) ^R(c)T (5) US(7)T (4)(6) IW(c) ^R(c)(8)T (7) IR(c)(9)T (3) (9) IQ(c) ^R(c)(10) (日x)(Q(x) ^R(x)T (9) EG
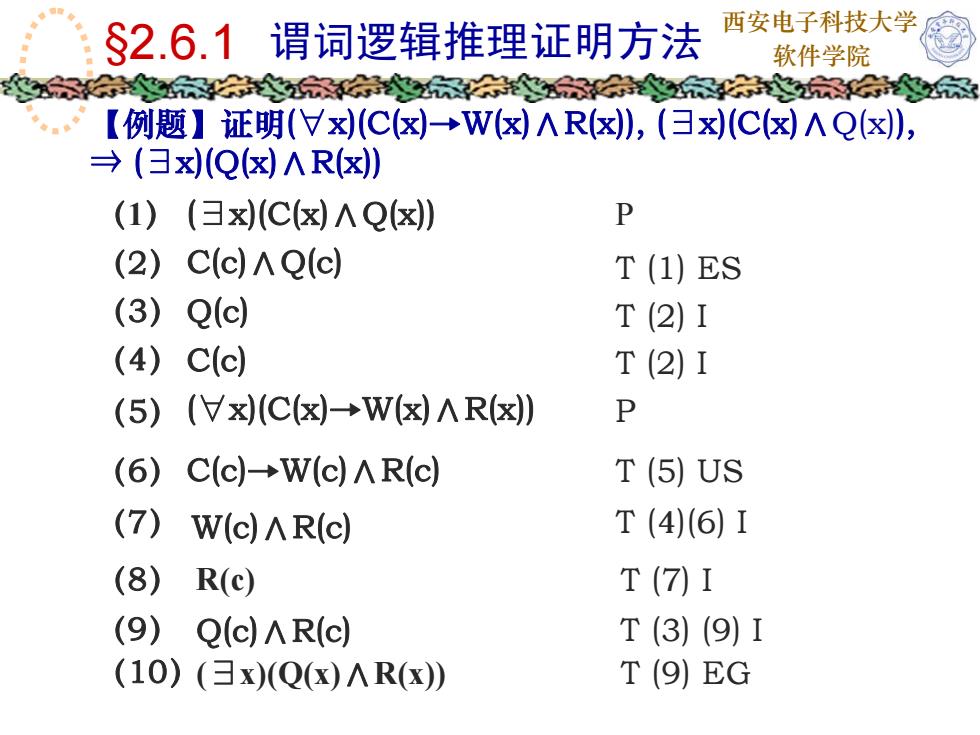
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明( ∀x)(C(x)→W(x)∧R(x)), ( ∃x)(C(x)∧Q(x)), ⇒ ( ∃x)(Q(x)∧R(x)) ( 1 ) ( ∃x)(C(x)∧Q(x)) P (2) T (1) ES (5) P (6) T (5) US (7) W(c)∧R(c) T (4)(6) I (8) R(c) T (7) I (3) T (2) I (4) T (2) I C(c)∧Q(c) Q(c) C(c) ( ∀x)(C(x)→W(x)∧R(x)) C(c)→W(c)∧R(c) (9) Q(c)∧R(c) T (3) (9) I (10) ( ∃x)(Q(x) ∧R(x)) T (9) EG

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院茶【例题】证明(Vx)(P(×)VQ(×))=(Vx)P() V (日x)Q(x)方法一、反证法(1)-((Vx)P(x) V(三x)Q(x)P(假设前提)(2) -(Vx) P(x) ^ -(三x)Q(x)T (1) E(3)-(Vx) P(x)T (2) I(4)(x)-P(x)T (3) E(5)- P(a)T (4) ESP(6)(Vx)(P(x) VQ(x))(7)T (6) USP(a) V Q(a)(8)Q(a)T (5)(7) I
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明 ( ∀x)(P(x)∨Q(x)) ⇒ ( ∀x)P(x)∨( ∃x)Q(x) 方法一、反证法 ( 1 ) ¬( ( ∀x)P(x) ∨ ( ∃x)Q(x)) P(假设前提 ) (2) ¬ ( ∀x) P(x) ∧ ¬ ( ∃x)Q(x) T (1) E (5) ¬ P(a) T (4) ES (6) ( ∀x)(P(x) ∨Q(x)) P (7) P(a) ∨Q(a)) T (6) US (8) Q(a)) T (5)(7) I (3) ¬ ( ∀x) P(x) T (2) I (4) ( ∃x) ¬P(x) T (3) E

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院-【例题)证明(Vx)(P(≤) VQ(×)=(Vx)P(×)V (x)Q(x)方法一、反证法(9) (日x)Q(β)T (8) EGT (2) I(10 -(3x)Q(x) (11 (3x)Q(x)△-(x)Q(x)矛盾)
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明 ( ∀x)(P(x)∨Q(x)) ⇒ ( ∀x)P(x)∨( ∃x)Q(x) 方法一、反证法 (9) ( ∃x)Q(x) T (8) EG (10 ) ¬ ( ∃x)Q(x) T (2) I (11 ) ( ∃x)Q(x) ∧ ¬ ( ∃x)Q(x) 矛盾