西安电子科技大学：《信号检测与估值》课程教学资源（课件讲稿，2019）第一章 高斯信道上的信号检测

最大似然准则 ·最大似然(ML)准则 >co=c1=0,c10=c01=1,且先验等概（即PHo)=PH)=1/2)时的 Bayest准则 >似然比检测门限 n2 P(Ho)(Co-Coo)_ P(H-1 P(H)(cor-cu)P(H) >判决准则 p>1 p(H jv.arg max P(rH) j=0,1 信号检测与估值2019年秋 16

最大似然准则 最大似然（ML）准则  c00=c11=0, c10=c01=1，且先验等概（即P(H0)=P(H1)=1/2）时的 Bayes准则  似然比检测门限           0 10 00 0 1 01 11 1 = 1 PH c c PH PH c c PH       判决准则 PH c c PH  1 01 11 1       1 1 1 H p rH  j Pr H  arg max ( | )   0 0 1 H p rH  0,1 arg max ( | ) ML j j j Pr H   信号检测与估值 2019年秋 16

MAP准则 ·最大后验概率(MAP)准则 >c1o-coo=co1-c时的Bayes准则 >似然比检测门限 P(H)(Go-cw)=P(Ho） ）P(H) >判决准则 7=P()(co-G p()>P(H) p(rH )P(H)>P(Ho)p(rHo) p(rH)<P(H) p(r) p(r) H。 Ho H p()p(H) jxup =argmax P(H,r) j=0,1 Ho 信号检测与估值2019年秋 17

MAP准则 最大后验概率（MAP）准则  c10-c00=c01-c11时的Bayes准则  似然比检测门限       判决准则           0 10 00 0 1 01 11 1 = PH c c PH PH c c PH             1 1 0 H p rH P H p rH P H           1 11 0 0 () () H p rH P H P H p rH pr pr       0 0 1 H p rH  P H 0 () () H pr pr      H1        0 1 0 H p Hr pH r     0,1 arg max | MAP j j j PH r   信号检测与估值 2019年秋 17

派生贝叶斯准则 ML:Co0=C11=0,C10=Co1=1, P(Ho)=P(H=1/2 MAEP:Coo=C11=0,C10=C01=1 MAP:C10-C0o=Co1-C11 信号检测与估值2019年秋 18

派生贝叶斯准则 ML:c00=c11=0, c10=c01=1， P(H 0)=P(H1 P(H 0) P(H1) 1/2 = MAEP: c00=c11=0, c10=c01=1 MAP: c10-c00=c01-c11 信号检测与估值 2019年秋 18

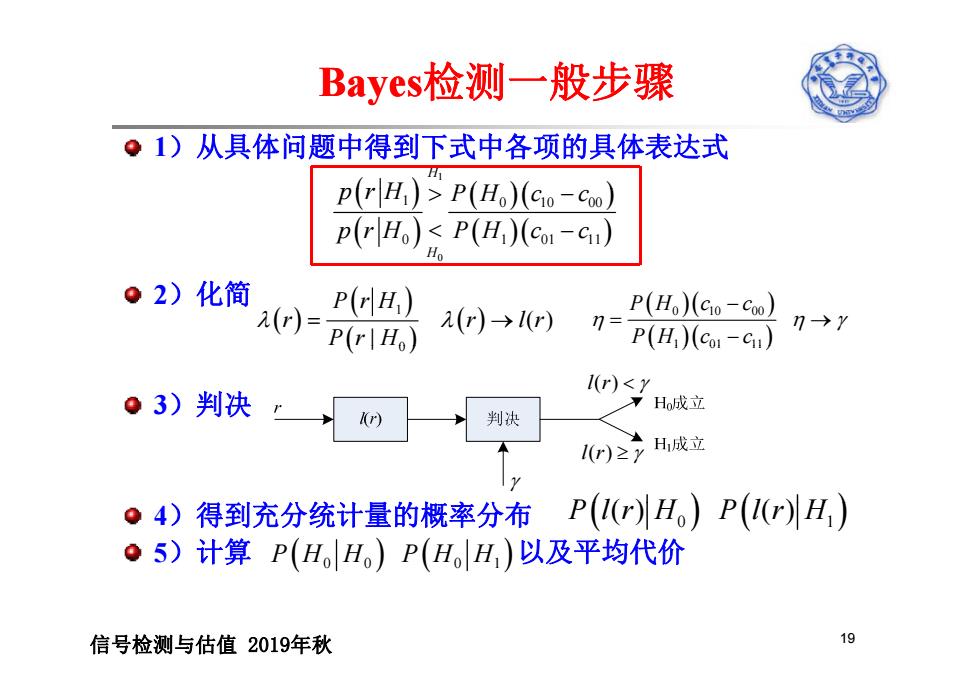
Bayes检测一般步骤 ·1)从具体问题中得到下式中各项的具体表达式 p(H）>P(Ho)(co-co） p(rHo)<P(H)(col-c) H ●2)化简 P(H) (r)=P(rIHo) (r）→1) n P(Ho)(Go-c0】 → P(H)(Co1-cu) 1(r)<Y 。3)判决 r H成立 r) 判决 1(r）≥y H成立 。4)得到充分统计量的概率分布P((r)H。)P((r)H,) ●5)计算P(H。H）P(HH,)以及平均代价 信号检测与估值2019年秋 19

Bayes检测一般步骤 1）从具体问题中得到下式中各项的具体表达式      H1 p rH    P H         0 1 0 10 00 0 1 01 11 H p rH P H c c p rH P Hc c     2）化简         10 () | P rH r r lr P r H           0 10 00 1 01 11 PH c c P Hc c        3）判决 l r( )    | 0   1 01 11   得到充分统计量的概率分布 l r( )    4）得到充分统计量的概率分布 Pl H Pl H  () ()    5）计算 以及平均代价 P l ( )r H Pl 0 1   ( )r H  PH H PH H  00 01    信号检测与估值 2019年秋 19

1.3二元实高斯信号检测 BPSK 0 o On-Off Keying 0 Binary Orthogonal Modulation 信号检测与估值2019年秋 20

1.3二元实高斯信号检测 BPSK 0 On-Off Keying 0 Binary Orthogonal Modulation 信号检测与估值 2019年秋 20 0