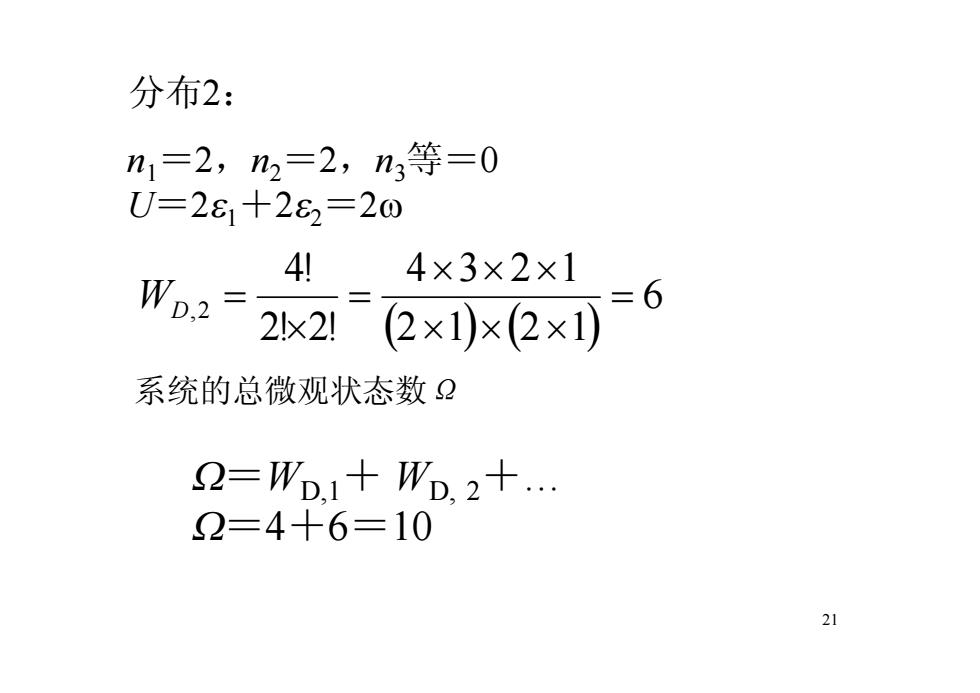
分布2: n1=2,n2=2,n3等=0 U=281+282=20 4 4×3×2×1 WD.2 =6 2x2!(2×1)×(2×1) 系统的总微观状态数2 2=Wb.1+Wb,2十 2=4十6=10 21
21 分布2: n1 =2,n2 =2,n3等=0 U=2e1+2e2 =2w ( ) ( ) 6 2 1 2 1 4 3 2 1 2! 2! 4! ,2 = ´ ´ ´ ´ ´ ´ = ´ WD = 系统的总微观状态数Ω W=WD,1+ WD, 2+. W=4+6=10

对于具有非简并能级的定域子系统的分布的微观 状态数WD Wp=CNC欢n N! (N-n)月 n(N-n)!n2(N-n1-n2)! N! N! WD二 Πn, 22
22 对于具有非简并能级的定域子系统的分布的微观 状态数WD LL !( )! ( )! !( )! ! 2 1 2 1 1 1 n N n n N n n N n N - - - × - = Õ = i ni N W ! ! D WD = CN n1 ×CN n2 -n1 LL Õ = = i i n N n n N ! ! ! ! ! 1 2 LL

对于具有简并能级的定域子系统的分布的微观状 态数WD W,=(gC)(g2Cm). N! =81”.8 n,ln2l. 形=T 23
23 对于具有简并能级的定域子系统的分布的微观状 态数WD WD = (g1 n1CN n1 )×(g2 n2CN n2 -n1 )LL úLL û ù ê ë é - - - × × ú û ù ê ë é - = × !( )! ( )! !( )! ! 2 1 2 1 2 1 1 1 1 2 n N n n N n g n N n N g n n LL LL ! ! ! 1 2 1 2 1 2 n n N g g n n = × × = Õ i i n i n W N i ! g ! D

例9.2.2 在例7.1中,当e,=0和当e,=ω的两个能 级分别为2度和3度简并时,试计算含有四个这样的分 子的系统总能量为2ω的总微观状态数2。 解: €4 =3w €3=2w €2=w e1=0 24
24 在例7.1中,当ε1 =0和当ε2 =ω的两个能 级分别为2度和3度简并时,试计算含有四个这样的分 子的系统总能量为2ω的总微观状态数Ω。 解: 例9.2.2

分布1: WD.1=4×(23)=4×8=32 分布2: WD2=6×(22)×(32)=6×36=216 系统的总微观状态数2 2=32+216=248 对于定域子系统分布的微观状态数W, g加n 25
25 分布1: WD,1 =4×(23 ) =4×8 =32 分布2: WD,2 =6×(22 ) ×(32 ) =6×36 = 216 系统的总微观状态数Ω W = 32+216 = 248 对于定域子系统分布的微观状态数WD ( ) = Õ i i n i n g W N i ! ! D