桃车伦与散理统针」 二维随机变量(X,Y)的分布律也可表示为 X 12 y -2-乃z-h2x-. Rr -yr- -Duy-py-
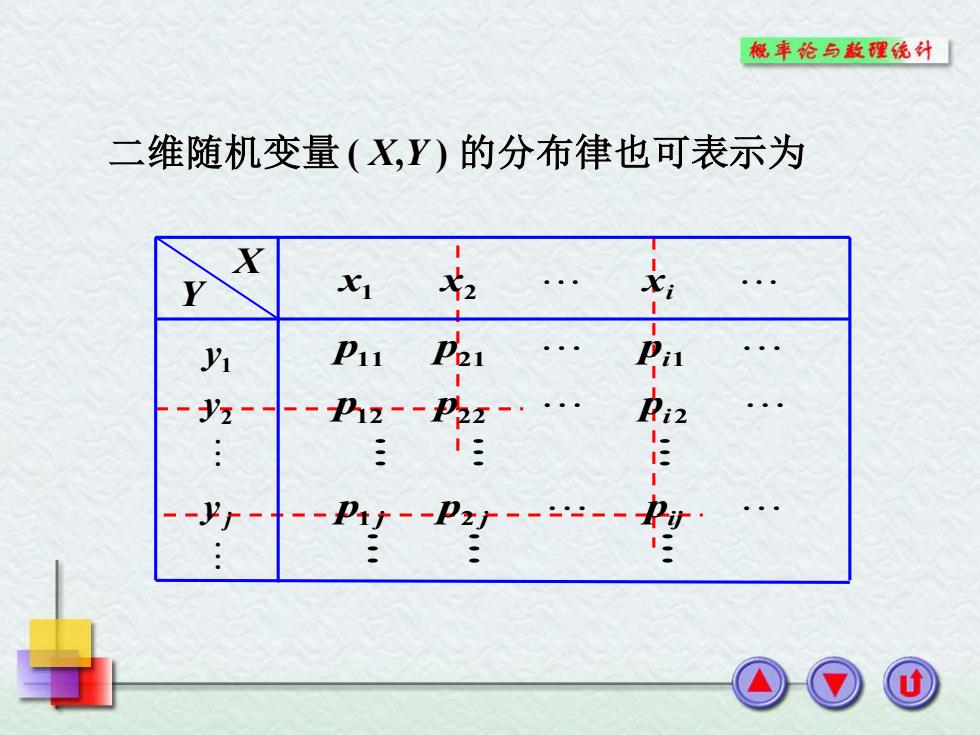
二维随机变量 ( X,Y ) 的分布律也可表示为 X Y x1 x2 xi j y y y 2 1 p11 p21 pi1 p12 p22 pi 2 p1 j p2 j pij

概率论与款程统针「 例1设随机变量X在1,2,3,4四个整数中等可能地 取值,另一个随机变量Y在1~X中等可能地取一 整数值.试求(X,Y)的分布律. 解{X=i,Y=}的取值情况是:i=1,2,3,4, 取不大于的正整数.且由乘法公式得 11 P(X=i,Y=i)=P(Y=jX=i)P(X=i= 4 i=1,2,3,4,j≤i. 于是(X,)的分布律为
. ( , ) . , 1 ~ 1,2,3,4 整数值 试求 的分布律 取值 另一个随机变量 在 中等可能地取一 设随机变量 在 四个整数中等可能地 X Y Y X X 解 {X = i,Y = j}的取值情况是: i = 1,2,3,4, j取不大于i的正整数. 且由乘法公式得 P{X = i,Y = j}= P{Y = j X = i}P{X = i} , 4 1 1 = i i = 1,2,3,4, j i. 于是 (X,Y )的分布律为 例1
概车纶与款理统外 3 4 1 1 12 16 1 1 1 2 0 8 12 16 1 1 3 0 0 12 16 1 4 0 0 0 16
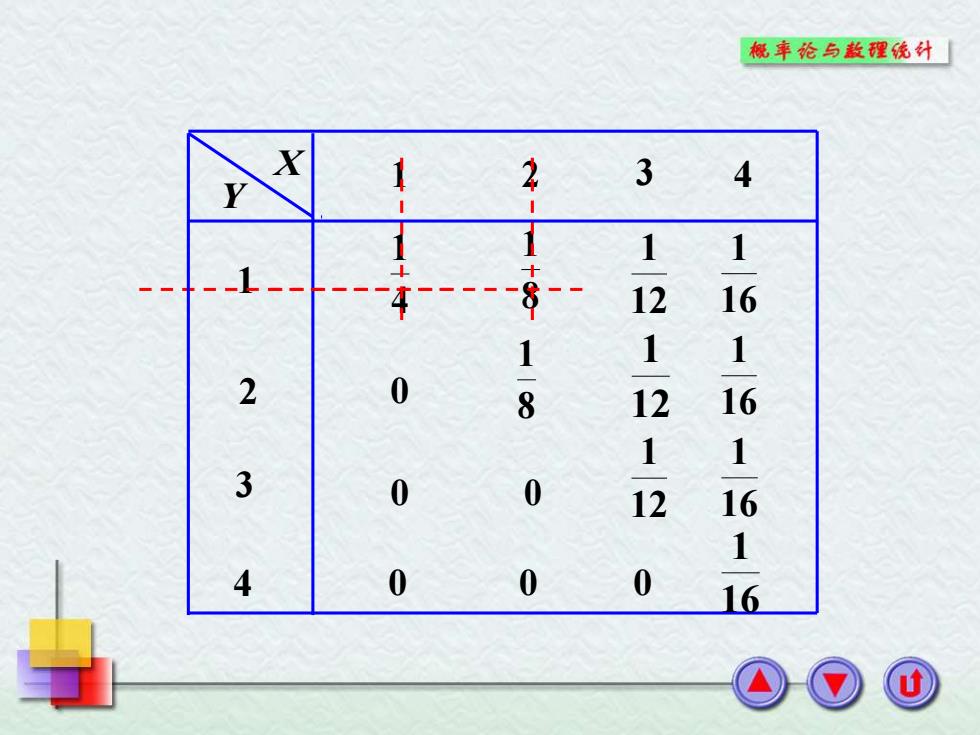
X Y 1 2 3 4 1 2 3 4 4 1 8 1 12 1 16 1 0 8 1 12 1 16 1 0 0 12 1 16 1 0 0 0 16 1