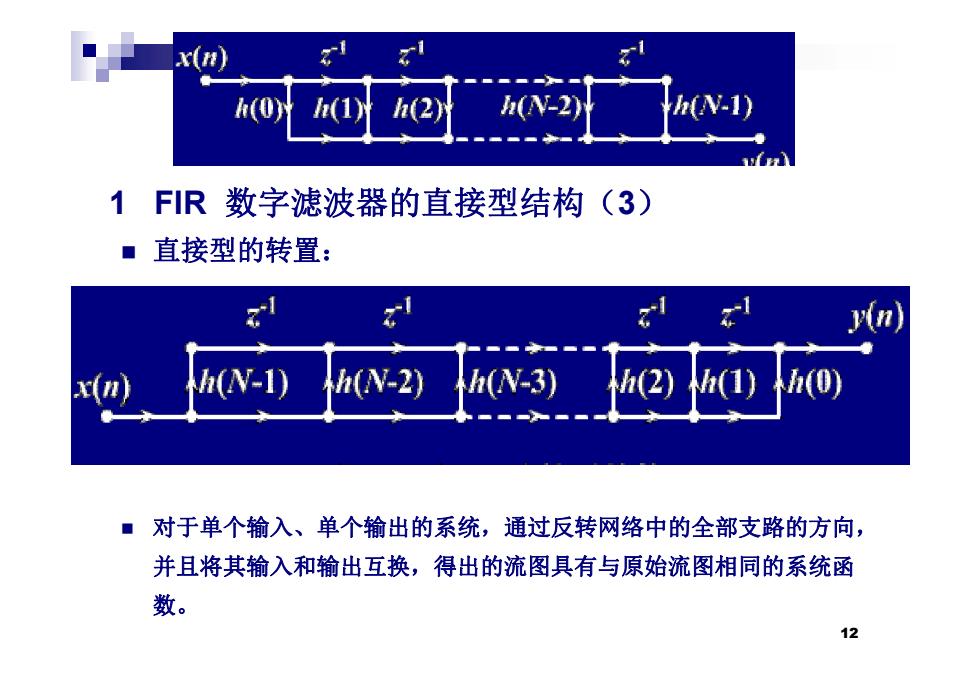
h(2 (N-2) h-1) 1FIR数字滤波器的直接型结构(3) ■直接型的转置: y(n) hN-1) hN-2) hN-3) h(2 ■对于单个输入、单个输出的系统,通过反转网络中的全部支路的方向, 并且将其输入和输出互换,得出的流图具有与原始流图相同的系统函 数。 12
1 FIR 数字滤波器的直接型结构 ( 3 ) 直接型的转置: 对于单个输入、单个输出的系统,通过反转网络中的全部支路的方向, 并且将其输入和输出互换,得出的流图具有与原始流图相同的系统函 数。 12
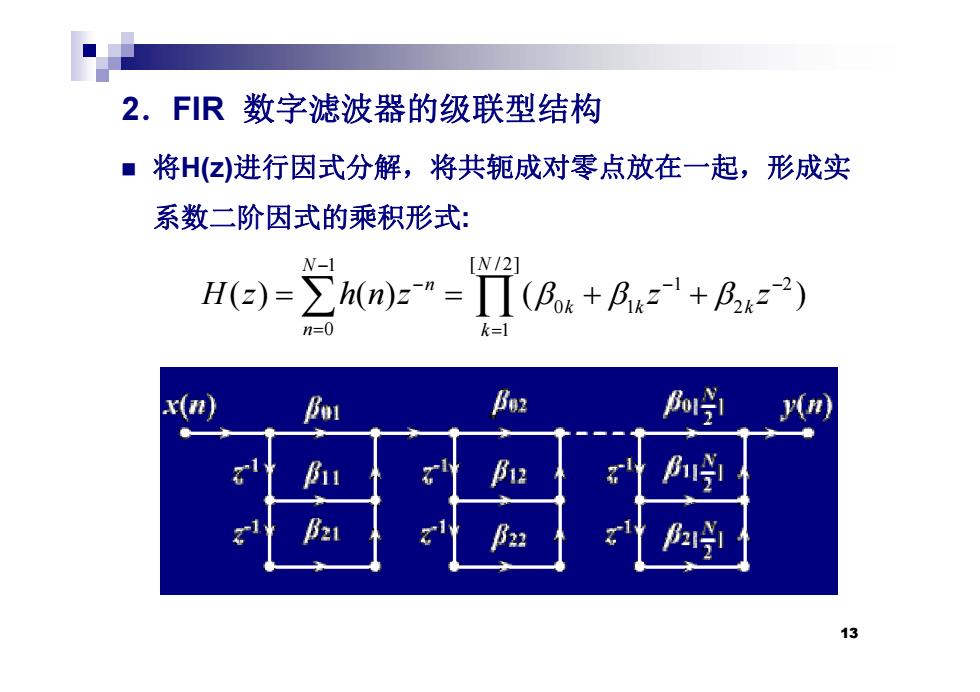
2.FR数字滤波器的级联型结构 ■将Hz)进行因式分解,将共轭成对零点放在一起,形成实 系数二阶因式的乘积形式: N-1 [N/2] H(z)=∑h(n)z"=Π(Bk+BA21+B22) n=0 k=1 Bu2 时i 1 B12 时 2阳 h的 13
2.FIR 数字滤波器的级联型结构 将H(z)进行因式分解,将共轭成对零点放在一起,形成实 系数二阶因式的乘积形式: N1 [ /2] N 1 2 01 2 0 1 () () ( ) N N n kk k n k H z hnz z z 13

2.FR数字滤波器的级联型结构(2) 级联型的特点 口每个一阶网络控制一个零点,每个二阶网络控制一对零 点,调节2或3个系数即可调整零点,便于控制滤波器的 传输零点 口系数比直接型多,所需的乘法运算多 ■例8.2.1(P218)画直接型和级联型结构 H(z)=0.96+2z1+2.8z2+1.5z3 H(z)=(0.6+0.5z1)1.6+2z1+3z2) 14
2.FIR 数字滤波器的级联型结构 数字滤波器的级联型结构(2) 级联型的特点 每个一阶网络控制一个零点,每个二阶网络控制一对零 点,调节2或3个系数即可调整零点 个系数即可调整零点,便于控制滤波器的 便于控制滤波器的 传输零点 系数比直接型多,所需的乘法运算多 例8.2.1(P218) 画直接型和级联型结构 123 Hz z z z ( ) 0.96 2 2.8 1.5 1 12 Hz z z z ( ) (0.6 0.5 )(1.6 2 3 ) 14

3.FIR滤波器的线性相位结构 H(e)=H(@)e) 第一类线性相位:以o)=一oN-」 2 第三类线性相位:6o)=一oN 2 ■FIR滤波器单位脉冲响应h(n)为实数,0≤n≤N-1且满足: 口第一类(偶对称):h(n)=h(N-1-n) o第二类(奇对称):h(n)=-h(N-1-n) 口对称中心在(N-1)/2处,这种FIR滤波器具有严格线性相位。 15
3.FIR滤波器的线性相位结构 ( ) ( ) ( ) j g j H(e ) H ( )e g N 1 2 - 第一类线性相位:( )=- 2 N 1 2 2 - 第二类线性相位:( )=- - FIR滤波器单位脉冲响应h(n)为实数, 且满足: 0 1 n N 第一类(偶对称): 第二类(奇对称) hn hN n () ( 1 ) 第二类(奇对称): hn hN n () ( 1 ) 对称中心在 (N-1) / 2处,这种FIR滤波器具有严格线性相位。 hn hN n () ( 1 ) 15

N为奇数时 N-1 e)2-空ma+宁,5 N-1 h(n)z-" n=0 令n=N-1-m N-11 空e0+三v-1a N-1- =名me+:-小9 +第一类 第二类 16
N为奇数时 1 () () N n H z hnz 1 1 2 1 1 2 1 () () N N N n n N hh h 0 () () n H z hnz 2 0 1 1 2 () () 2 n n n N n h n z h z h n z 令nN m 1 1 1 1 1 N N 1 2 2 2 (1) 0 0 1 2 () ( 1 ) N n Nm n m hn hN m N zh z z 1 1 1 2 ( 1) 2 1 ( ) N N n Nn N h h ( 1) 2 0 1 ( ) 2 n Nn n N h nz z h z + 第一类 — 第二类 16