西安电子科技大学：《数字信号处理》课程教学课件（讲稿）03 离散傅里叶变换DFT及其快速算法FFT

问题： ■序列的傅里叶变换、Z变换是时域离散信号及系统分析与 设计的重要数学工具； ■但变换结果均为连续函数，无法用计算机进行处理； ■离散傅里叶变换(DFT)对有限长时域离散信号的频谱进 行等间隔采样，频域函数被离散化了，便于信号的计算机 处理。 ■DFT运算量较大，快速离散傅里叶变换算法(FFT)是解 决方案 2

问题:  序列的傅里叶变换、Z变换是时域离散信号及系统分析与 设计的重要数学工具；  但变换结果均为连续函数，无法用计算机进行处理；  离散傅里叶变换（DFT）对有限长时域离散信号的频谱进 行等间隔采样，频域函数被离散化了，便于信号的计算机 处理。  DFT运算量较大，快速离散傅里叶变换算法（FFT）是解 决方案 2

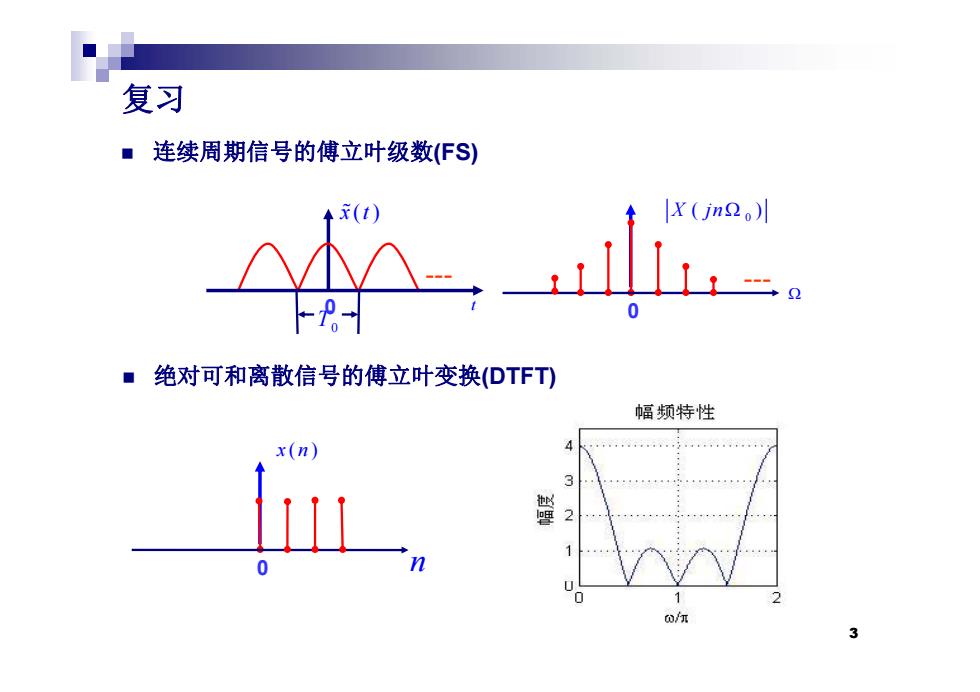
复习 ■连续周期信号的傅立叶级数(FS) x(jn2o)川 ■绝对可和离散信号的傅立叶变换(DTFT) 幅频特性 7 o/n 3

复习  连续周期信号的傅立叶级数(FS) 0 x ( )t X jn ( )   - T00 t 0 -  绝对可和离散信号的傅立叶变换(DTFT) x ( ) n 0 n 3

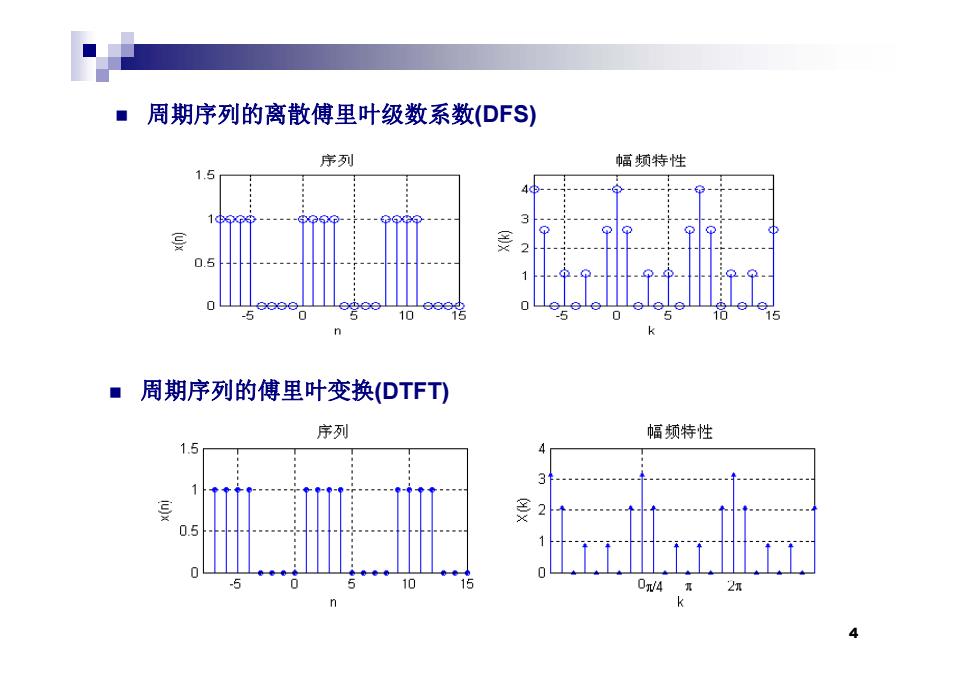
◆ 周期序列的离散傅里叶级数系数(DFS) 序列 幅频特性 15 -5 10 ■周期序列的傅里叶变换(DTFT) 序列 幅频特性 1.5 10 0/4

 周期序列的离散傅里叶级数系数(DFS)  周期序列的傅里叶变换(DTFT) 4

3.1离散傅里叶变换(DFT)的定义 ■3.1.1DFT的定义 设xn)是一个长度为M的有限长序列，)的N点离散傅立叶变换： XW=DFT(-∑0me号 N 0≤k≤N-1 三0 口N称为DFT变换区间长度，N≥M ·令w=e贤 (简化书写) ■离散傅立叶变换与逆变换对为： X)=DFTO])-分0mw0≤k≤N-1 n=0 o=Tx-三r传g 0≤n≤N-1

3.1离散傅里叶变换 离散傅里叶变换( ) DFT 的定义  3.1.1 DFT的定义 设x(n)是一个长度为M的有限长序列，x(n)的N点离散傅立叶变换： 1 2j ( ) [ ( )] ( )e 0 1 N kn N X k DFT x n x n k N          N称为DFT变换区间长度， 0 ( ) [ ( )] ( )e 0 1 N n X k DFT x n x n k N      N M  令 （简化书写）  离散傅立叶变换与逆变换对为： 2j N W e N     离散傅立叶变换与逆变换对为： 1 ( ) [ ( )] ( ) 0 1 N kn X k DFT x n x n W k N N       0 N n 1 1 ( ) [ ( )] ( ) 0 1 N kn N x n IDFT X k X k W n N N        5 0 N N k

X(A)-DFTI-0sN-1 证明： DFTx=芝Xkw N K=0 x(m)WkW Nk=0 m=0 N-I 1 N-I wk(m-n) 由于 W)= 1, m-n=MN,M为整数 e N 0, m-n≠MN,M为整数 于是 N- IDFT[X(k)]=∑x(m)6(m-m)=x(n)0≤n≤N-1 m=0 因此离散傅立叶逆变换是唯一的 6

证明 N -1 1 kn  1 0 ( ) [ ( )] ( ) 0 1 N kn N n X k DFT x n x n W k N        证明： IDFT[ ] ( ) -kn N k=0 1 X(k) X k W N   -1 1 1 [ ] N N- mk -kn   ( )W W =0 =0 [ ] mk kn N N k m x(m)W W N    ( ) ( ) N -1 N -1 1 k m-n    xm W 由于 ( ) N m=0 k=0 xm W N    由于 N1 1 2 ( ) ( ) k0 0 1 0 N j km n k m-n N N k 1 1 m n MN,M W e= N N m n MN,M                 ， 为整数 ， 为整数 于是 1 IDFT[ ( )]= ( ) ( ) N X k xm m n        xn n N () 0 1  因此离散傅立叶逆变换是唯一的 m0  xn n N () 0 1   6 因此离散傅 叶逆变换是唯 的