
(二)信度的估计方法 口同质性信度 也叫内部一致性信度,是指测验内部所有题目间的一致性程 度。题目间的一致性含有两层意思:其一是指所有题日测的 是同一种心理特质;其二是指所有题目得分之间都具有较高 的正相关。 因此,当一个测验具有较高的同质性信度时,说明测验要测 的是某一单个心理特质,实测结果就是该特质水平的反映; 如果一个测验同质性信度不高,则说明测验结果可能是几种 心理特质的综合反映,这时,测验结果不好解释。 估计同质性信度的方法主要有:分半信度、库德一理查逊信 度、克龙巴赫a系数
同质性信度 也叫内部一致性信度,是指测验内部所有题目间的一致性程 度。题目间的一致性含有两层意思:其一是指所有题目测的 是同一种心理特质;其二是指所有题目得分之间都具有较高 的正相关。 因此,当一个测验具有较高的同质性信度时,说明测验要测 的是某一单个心理特质,实测结果就是该特质水平的反映; 如果一个测验同质性信度不高,则说明测验结果可能是几种 心理特质的综合反映,这时,测验结果不好解释。 估计同质性信度的方法主要有:分半信度、库德-理查逊信 度、克龙巴赫α系数。 (二)信度的估计方法

估计同质性信度的方法: (1)分半信度 ◆指的是将每一个被试的测验分数按测题分成两部分,然后用 每个被试在两半测验上的得分求出整个测验的信度。 ◆计算不难,把对等的两半测验看成是在最短时间距离内施测 的两个平行测验。难的是,如何将测验分成相等的两半。 按题号的奇偶分半、按题且的难易程度分半、按题且的内容 分半等等。 ◆实际应用中,由于题目一般依据难度大小排列,采用奇偶分 半可使两半测验的题目在难度上基本相等,因此常被采纳。 如果一个测验无法分成对等的两半,则不宜使用分半信度
估计同质性信度的方法: (1)分半信度 ◆ 指的是将每一个被试的测验分数按测题分成两部分,然后用 每个被试在两半测验上的得分求出整个测验的信度。 ◆ 计算不难,把对等的两半测验看成是在最短时间距离内施测 的两个平行测验。难的是,如何将测验分成相等的两半。 按题号的奇偶分半、按题目的难易程度分半、按题目的内容 分半等等。 ◆ 实际应用中,由于题目一般依据难度大小排列,采用奇偶分 半可使两半测验的题目在难度上基本相等,因此常被采纳。 如果一个测验无法分成对等的两半,则不宜使用分半信度

每个被试的奇数 题/偶数题总分 由于分半信计算的是两个“半测验上得分的相关系数,只 是半个测验的信度,(测验越长信度越高),因此必须用斯皮尔 曼一布朗公式加以校正: Tsx 2r/(1+ron) 式中,r为整个测验的信度系数,为两个“半测验”上得 分的相关系数。 例4: 15名被试在奇偶分半测验上的得分 被试 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 奇数题 20 18 23 21 17 18 20 17 16 13 14 13 12 8 偶数题 20 22 19 22 18 15 14 17 15 16 14 12 10 7 6 计算两个“半测验”得分的积差相关系数为:0.86。代入公式 得:r=2rh/1+)=(2×0.86)/(+0.86)=0.92
由于分半信计算的是两个“半测验”上得分的相关系数,只 是半个测验的信度,(测验越长信度越高),因此必须用斯皮尔 曼-布朗公式加以校正: 式中,rxx为整个测验的信度系数,rhh为两个“半测验”上得 分的相关系数。 例4: 15名被试在奇偶分半测验上的得分 ( ) xx hh hh r = 2r 1+ r 被试 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 奇数题 20 18 23 21 17 18 20 17 16 13 14 13 12 8 8 偶数题 20 22 19 22 18 15 14 17 15 16 14 12 10 7 6 计算两个“半测验”得分的积差相关系数为:0.86。代入公式 得: rxx = 2rh h (1+ rh h ) = (2 0.86) (1+ 0.86) = 0.92 每个被试的奇数 题/偶数题总分

估计同质性信度的方法: (2)库德一理查逊信度 该方法适合于测验题目全部为二分计分题的测验的内部一 致性信度分析。库德一理查逊公式有好几个,常用的是下 面两个公式。 KRo公式: K「1-∑P,9 S? 式中,KR2为测验的信度,K为题目数,P和q分别表示答对和答错第道 题的被试人数比例,Sx表示所有被试在整个测验上的总得分的方差。 KR公式: 式中,KR2,为测验的信度,K为题目数,X表示所有被试在整个测验上的总 得分的均值
估计同质性信度的方法: (2)库德-理查逊信度 该方法适合于测验题目全部为二分计分题的测验的内部一 致性信度分析。库德-理查逊公式有好几个,常用的是下 面两个公式。 − − = 2 0 2 0 2 1 1 X i i S p q K K KR 公式: KR ( ) − − − = 2 1 2 1 2 1 1 KSX X K X K K KR 公式: KR 式中,KR20为测验的信度,K为题目数,pi和qi分别表示答对和答错第i 道 题的被试人数比例,SX 2表示所有被试在整个测验上的总得分的方差。 式中,KR21为测验的信度,K为题目数, 表示所有被试在整个测验上的总 得分的均值。 X
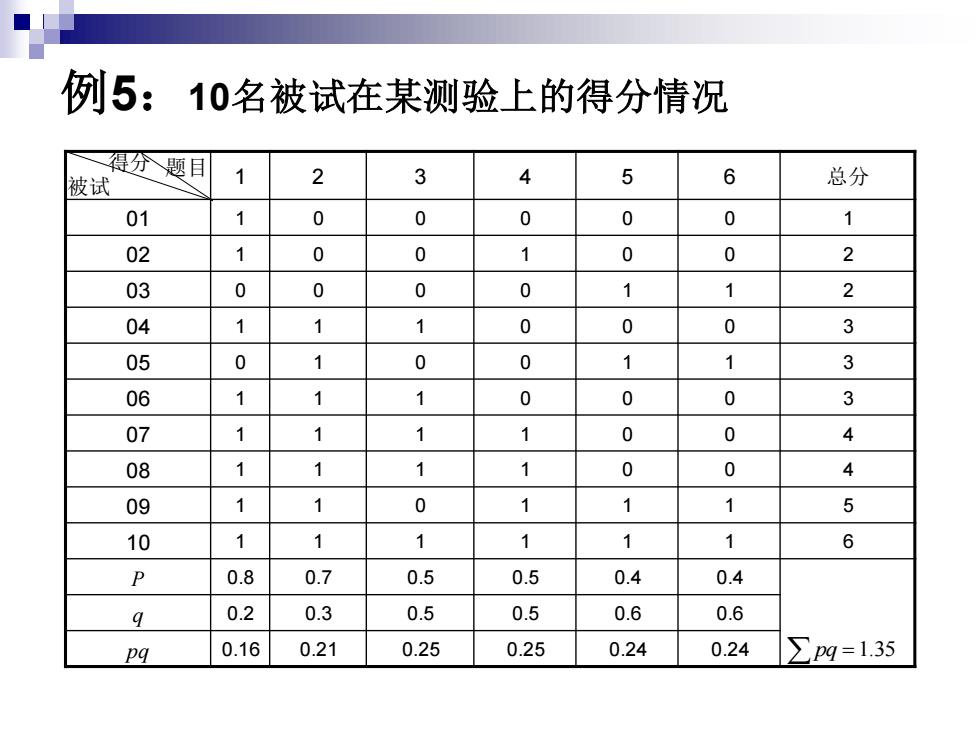
例5:10名被试在某测验上的得分情况 得分题目 被试 1 2 3 4 5 6 总分 01 0 0 0 0 0 1 02 0 0 7 0 0 03 0 0 0 0 1 1 2 04 1 1 1 0 0 0 3 05 7 0 0 1 3 06 1 1 1 0 0 0 3 07 1 1 1 1 0 0 4 08 7 7 0 0 4 09 1 0 1 1 1 5 10 1 1 1 1 1 1 6 P 0.8 0.7 0.5 0.5 0.4 0.4 9 0.2 0.3 0.5 0.5 0.6 0.6 pq 0.16 0.21 0.25 0.25 0.24 0.24 ∑Ppg=1.35
例5:10名被试在某测验上的得分情况 1 2 3 4 5 6 总分 01 1 0 0 0 0 0 1 02 1 0 0 1 0 0 2 03 0 0 0 0 1 1 2 04 1 1 1 0 0 0 3 05 0 1 0 0 1 1 3 06 1 1 1 0 0 0 3 07 1 1 1 1 0 0 4 08 1 1 1 1 0 0 4 09 1 1 0 1 1 1 5 10 1 1 1 1 1 1 6 P 0.8 0.7 0.5 0.5 0.4 0.4 q 0.2 0.3 0.5 0.5 0.6 0.6 pq 0.16 0.21 0.25 0.25 0.24 0.24 被试 pq =1.35 得分 题目