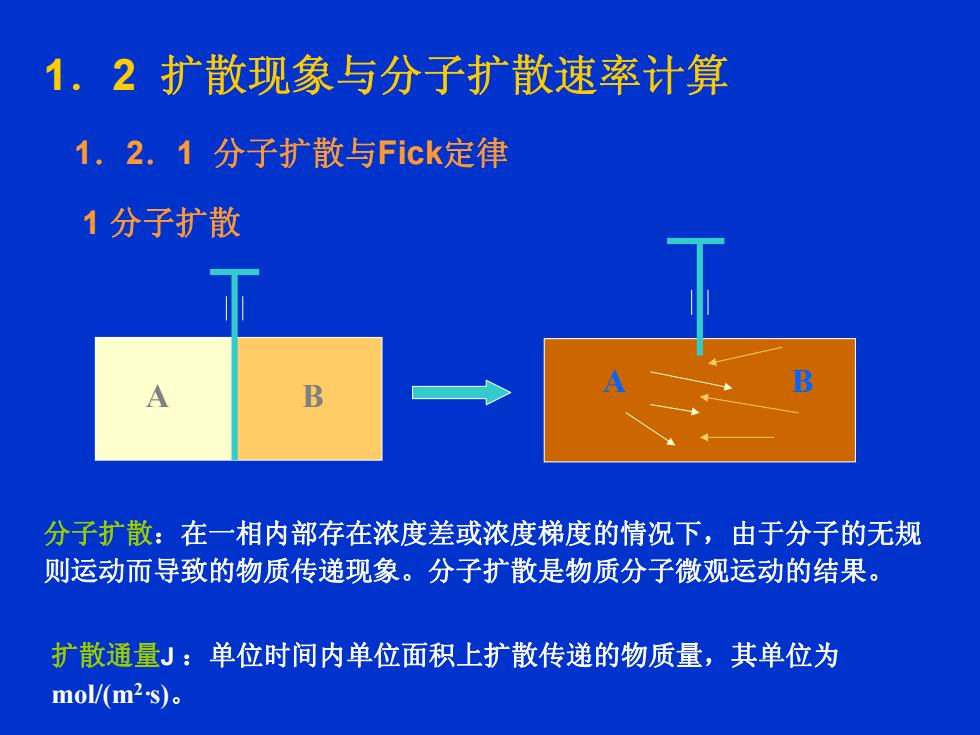
1.2扩散现象与分子扩散速率计算1.2.1分子扩散与Fick定律1分子扩散B分子扩散:在一相内部存在浓度差或浓度梯度的情况下,由于分子的无规则运动而导致的物质传递现象。分子扩散是物质分子微观运动的结果扩散通量J:单位时间内单位面积上扩散传递的物质量,其单位为mol/(m2-s)
A B A B A B A B 分子扩散:在一相内部存在浓度差或浓度梯度的情况下,由于分子的无规 则运动而导致的物质传递现象。分子扩散是物质分子微观运动的结果。 扩散通量J :单位时间内单位面积上扩散传递的物质量,其单位为 mol/(m2·s)。 1.2 扩散现象与分子扩散速率计算 1.2.1 分子扩散与Fick定律 1 分子扩散

2菲克(Fick)定律当物质A在介质B中发生扩散时,任一点处物质A的扩散通量与该位置上A的浓度梯度成正比,即:dtq=-元dcdxABdz傅立叶定律式中物质A在z方向上的分子扩散通量,kmol/(m?s)JduT=u物质A的浓度梯度,kmol/m4dCdz牛dyDAB物质A在介质B中的分子扩散系数,m?/s牛顿粘性定律负号一表示扩散是沿着物质A浓度降低的方向进行的。dc式中:DRA-B组分在A和B的混合物中同样,对B组分有-DBA的扩散系数。当扩散发生在理想气体或理想溶液中时,有DAB=DBA=D,故以后用D表示双组分物系的扩散系数
dz dC DJ A A −= AB 式中 JA——物质A在z方向上的分子扩散通量,kmol/(m2s) dCA/dz——物质A的浓度梯度,kmol/m4 DAB——物质A在介质B中的分子扩散系数,m2/s 负号——表示扩散是沿着物质A浓度降低的方向进行的。 当物质A在介质B中发生扩散时,任一点处物质A的扩散通 量与该位置上A的浓度梯度成正比,即: 2 菲克(Fick)定律 傅立叶定律 牛顿粘性定律 同样,对B组分有 dz dC DJ B B −= BA 式中:DBA-B组分在A和B的混合物中 的扩散系数。 当扩散发生在理想气体或理想溶液中时, 有DAB=DBA=D, 故以后用D表示双组分物系的扩散系数。 dx dt q −= λ dy du ±= μτ
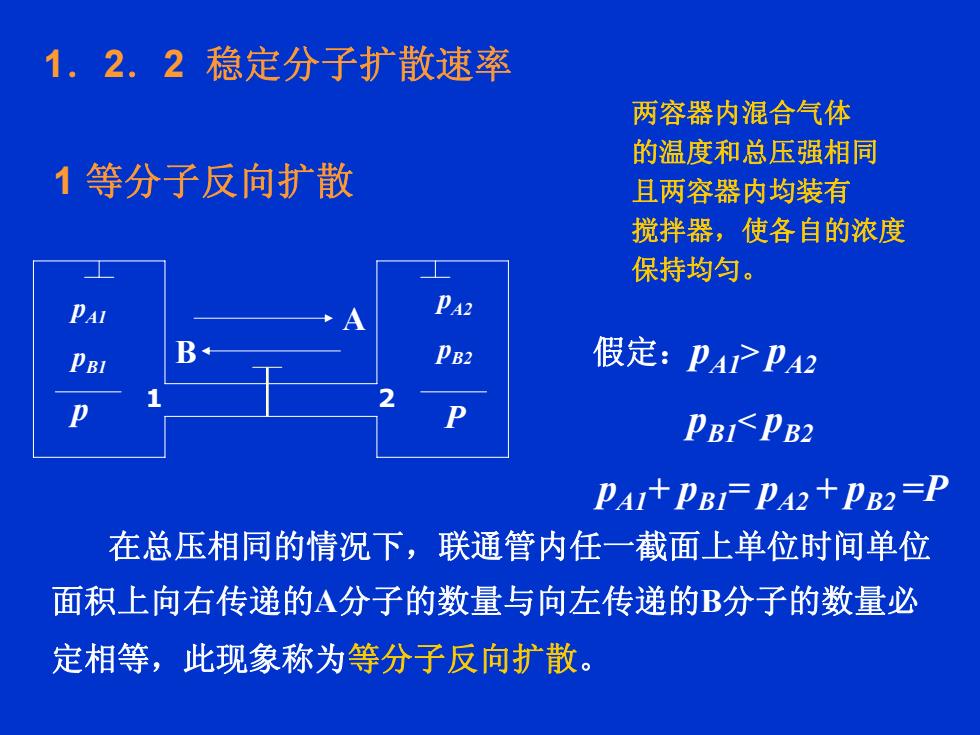
1.2.2稳定分子扩散速率两容器内混合气体的温度和总压强相同1等分子反向扩散且两容器内均装有搅拌器,使各自的浓度保持均匀。PA2PAI假定:PAPA2PB2PB1?PDPBI<PB2PAI+ PBI- PA2 + PB2 =P在总压相同的情况下,联通管内任一截面上单位时间单位面积上向右传递的A分子的数量与向左传递的B分子的数量必定相等,此现象称为等分子反向扩散
假定:pA1> pA2 pB1< pB2 pA1+ pB1= pA2 + pB2 =P pA1 pB1 pA2 pB2 p P A B 1 2 1 等分子反向扩散 两容器内混合气体 的温度和总压强相同 且两容器内均装有 搅拌器,使各自的浓度 保持均匀。 1.2.2 稳定分子扩散速率 在总压相同的情况下,联通管内任一截面上单位时间单位 面积上向右传递的A分子的数量与向左传递的B分子的数量必 定相等,此现象称为等分子反向扩散

J=-JB对于等分子反向扩散在任一固定的空间位置垂直于扩散方向的截面上,单位时间通过单位面积的A物质的量,称为A的传递速率,以N表示。对于单纯的等分子反向扩散,物质A的传递速率应等于A的扩散通量。DdpNa=J=-RTdzdz注意:在上述条件下,扩散为稳定过程,N为常数;PA一z呈线性关系。适于描述理想的精馏过程中的传质速率关系
在任一固定的空间位置垂直于扩散方向的截面上,单位时 间通过单位面积的 A物质的量,称为 A 的传递速率,以 N A 表 示。 对于单纯的等分子反向扩散,物质 A的传递速率应等于 A 的 扩散通量 。 对于等分子反向扩散 JA= - JB dz dp RT D dz dC DJN A A AA −=−== 注意:在上述条件下,扩散为稳定过程, NA为常数; pA—z呈线性关系。 适于描述理想的精馏过程中的传质速率关系

PPA1PB2PA2PB112Z上式分离变量并积分,积分条件为:Z=0,PA-PA1;Z2-Z,PA=PA2(7-4)A1-PA2RT2式中R为通用气体常数,R=8.314J/(mol.K)。注意:由于N(J)的单位用kmol/(m2.s),为与之相对应,气体的压强需用kPa
上式分离变量并积分, 积分条件为: z 1=0 , p A=pA1 ; z 2=z , p A=pA2 )( A pp AA 21 RTz D N = − P pA1 pB1 z 1 P pB2 pA2 z 2 (7-4) 式中 R为通用气体常数,R=8.314J/(mol.K) 。 注意:由于 N A ( J A)的单位用kmol/(m 2.s) , 为与之相对应,气体的压强需用kPa