
Clausius根据可逆过程的热温商值决定于始终态而 与可逆过程无关这一事实定义了“熵”(entropy)这 个函数,用符号“S表示,单位为:JK 设始、终态A,B的熵分别为S和S,则: S-S=aS=号). 或 δQR 对微小变化 T 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量
Clausius根据可逆过程的热温商值决定于始终态而 与可逆过程无关这一事实定义了“熵”(entropy)这 个函数,用符号“S”表示,单位为: 1 J K− ⋅ 这几个熵变的计算式习惯上称为熵的定义式, 即熵的变化值可用可逆过程的热温商值来衡量。 B B A R A ( ) Q S S S Tδ − = ∆ = ∫ R ( )i i i Q S T δ 或 ∆ = ∑ 设始、终态A,B的熵分别为SA和 SB,则: 对微小变化 TQ S R δ d =

3.3.4 Clausius不等式 设温度相同的两个高、低温热源间有一个可逆 机和一个不可逆机。 g= g+Q=1+ 0. T 则: 9. 9. T T 根据卡诺定理:7<7 则 2+g<0 TTh 推广为与多个热源接触的任意不可逆过程得:
3.3.4 Clausius 不等式 设温度相同的两个高、低温热源间有一个可逆 机和一个不可逆机。 h c h h c R 1 TT T T T = − − η = 根据卡诺定理:ηir< ηr h c h h c IR 1 QQ Q Q Q = + + 则: η = 0 h h c c + < T Q T Q 则 推广为与多个热源接触的任意不可逆过程得: 0 δ ir < ⎟⎟⎠⎞ ⎜⎜⎝⎛∑i i i TQ
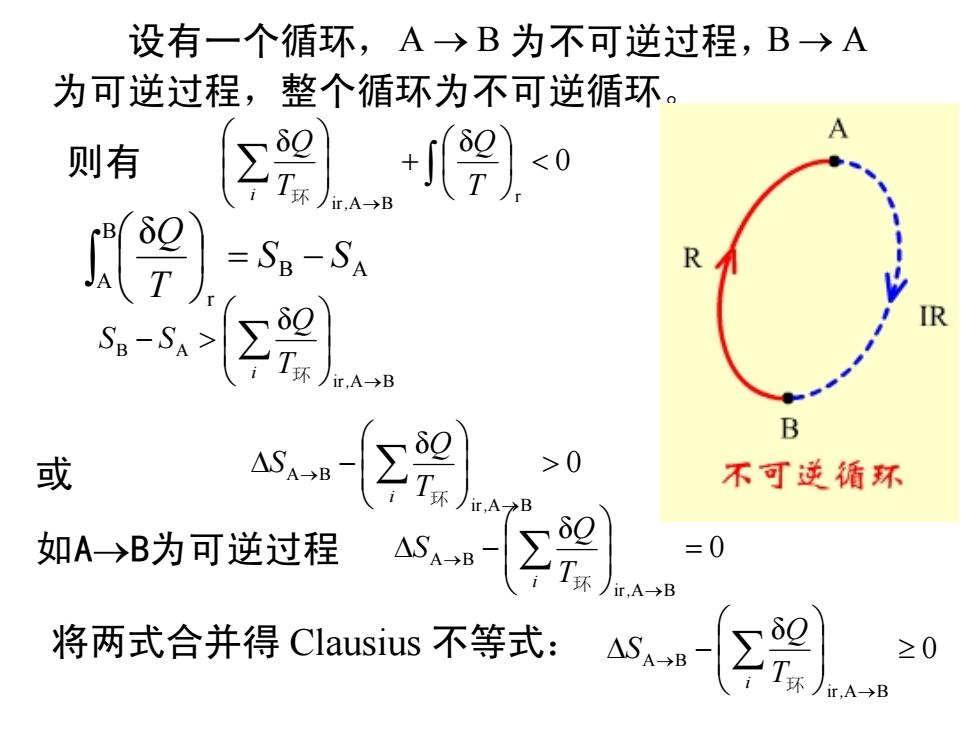
设有一个循环,A→B为不可逆过程,B→A 为可逆过程,整个循环为不可逆循环。 A 则有 =SB-SA R Sn-S> B 或 不可逆循环 如A→B为可逆过程 =0 ir,A→B 将两式合并得Clausius不等式:ASB-∑元., ≥0
设有一个循环, 为不可逆过程, 为可逆过程,整个循环为不可逆循环。 A B → B A → 则有 0 δ δ r ir A B ⎟ < ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∑ ∫ → T Q T Q , i 环 ir A B B A δ → ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − > ∑ , i T Q S S 环 或 0 δ ir A B A B > ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − → → ∑ , i T Q S 环 如A →B为可逆过程 0 δ ir A B A B = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − → → ∑ , i T Q S 环 将两式合并得 Clausius 不等式: 0 δ ir A B A B ≥ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − → → ∑ , i T Q S 环 B A B A r δ S S T Q ⎟ = − ⎠ ⎞ ⎜ ⎝ ⎛ ∫

ASA- ≥0 ir,A→B δQ是实际过程的热效应,T环是环境温度。若是 不可逆过程,用>”号,可逆过程用=号,这时环 境与体系温度相同。 对于微小变化: d、 T环 dS≥ δ9 或 这些都称为Clausius不等式,也可作为热力 学第二定律的数学表达式
0 δ ir A B A B ≥ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − → → ∑ , i T Q S 环 是实际过程的热效应, T环是环境温度。若是 不可逆过程,用 “ > ”号,可逆过程用 “ = ”号,这时环 境与体系温度相同。 δ Q 对于微小变化: 0 δ d − ≥ T环 Q S 或 T环 Q S δ d ≥ 这些都称为 Clausius 不等式,也可作为热力 学第二定律的数学表达式

Clausius不等式的意义 Clsusius不等式引进的不等号,在热力学上可以作 为变化方向与限度的判据。 dS≥ δ0 >”号为不可逆过程 乐 =”号为可逆过程 dS隔 ≥0 >”号为自发过程 =”号为处于平衡状态 因为隔离系统中一旦发生一个不可逆过程,则一定 是自发过程
Clausius 不等式的意义 Clsusius 不等式引进的不等号,在热力学上可以作 为变化方向与限度的判据。 “>” 号为不可逆过程 T环 “=” 号为可逆过程 Q S δ d ≥ “>” 号为自发过程 “=” 号为处于平衡状态 dS隔离 ≥ 0 因为隔离系统中一旦发生一个不可逆过程,则一定 是自发过程