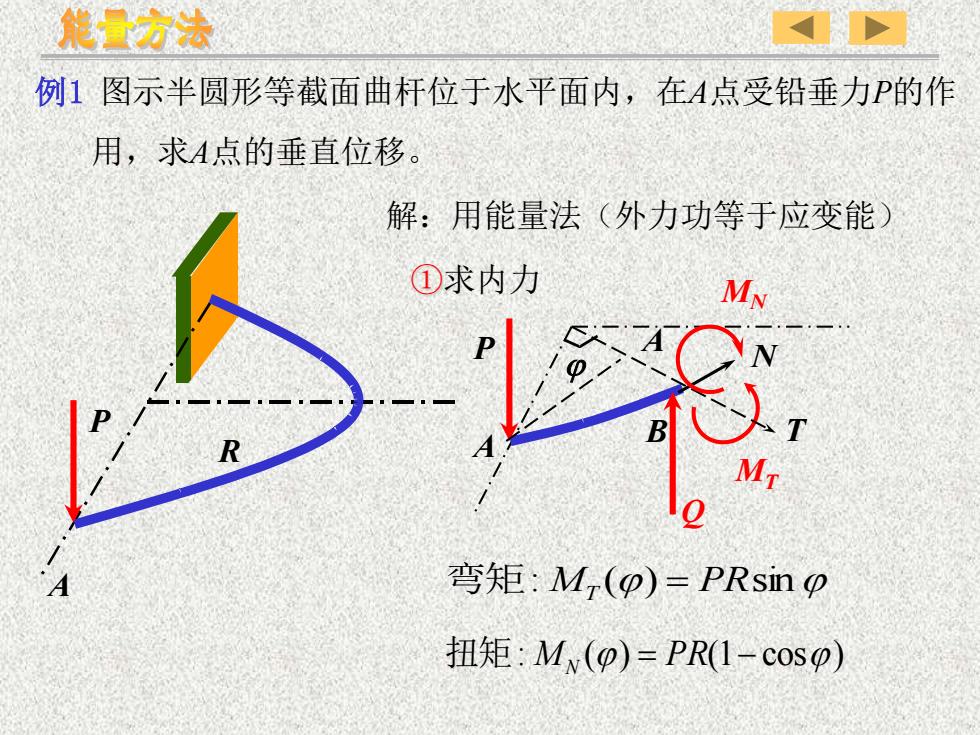
能量方法例1图示半圆形等截面曲杆位于水平面内,在A点受铅垂力P的作用,求A点的垂直位移。解:用能量法(外力功等于应变能)①求内力MNRM.7弯矩:M,(β)=PRsin A扭矩:M (β)= PR(1-cosβ)
Q MN MT A A P N B j T 例1 图示半圆形等截面曲杆位于水平面内,在A点受铅垂力P的作 用,求A点的垂直位移。 解:用能量法(外力功等于应变能) ①求内力 弯矩: MT (j) = PRsinj : M (j) = PR(1− cosj) 扭矩 N A P R

能量方法②变形能:dx12EA2E1PRa-oso)Rdo+PRsn)Rdo元Jo2GIp2EIP2R元3P2R元4GIp4EI③外力功等于应变能3PR元PR元P:. f4.W.f=U2EI2GIp2
③外力功等于应变能 ②变形能: = + + L L P L x EI M x x G I M x x EA N x U d 2 ( ) d 2 ( ) d 2 ( ) 2 2 n 2 + − = j j j j 0 2 2 2 0 2 2 2 d 2 (sin ) d 2 (1 cos ) R EI P R R GI P R P EI P R GI P R 4 P 4 3 2 3 2 3 = + f U P W = A = 2 EI PR GI PR f P A 2 2 3 3 3 = +
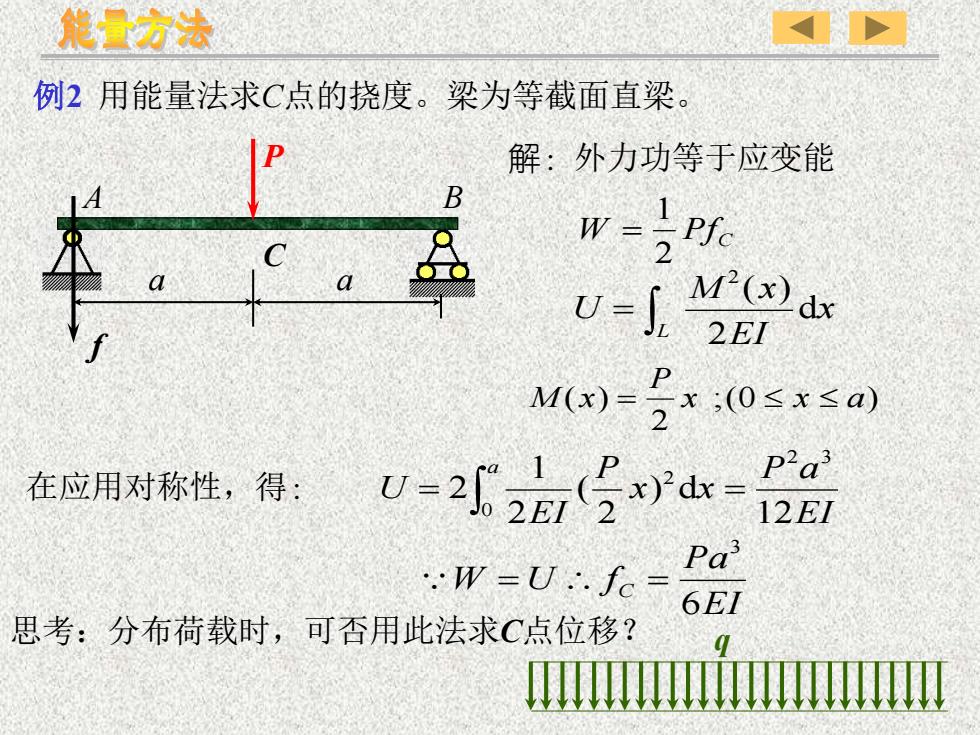
能量方法例2用能量法求C点的挠度。梁为等截面直梁A解:外力功等于应变能PBLA1SPrW=RA2M(x) dxU-I.2EIAM(x) =*;(0≤≤a)PaL(Px)dx=U = 2]。.2F在应用对称性,得:2.EI212EIPa3w-U..fc -16EI思考:分布荷载时,可否用此法求C点位移?q
例2 用能量法求C点的挠度。梁为等截面直梁。 W PfC 2 1 = 解:外力功等于应变能 = L x EI M x U d 2 ( ) 2 ;(0 ) 2 ( ) x x a P M x = 在应用对称性,得: EI P a x x P EI U a 12 ) d 2 ( 2 1 2 2 3 0 2 = = EI Pa W U f C 6 3 = = 思考:分布荷载时,可否用此法求C点位移? q C a a A P B f

能量方法$11-2莫尔定理(单位力法)定理的证明:V求任意点A的位移f,HfHMe(x) dx图aU-J.[Po=12EIM(x) dxU。-J.2EI.R[M(x)+ M.(x))dxUc=图b2EIP=1g(VUc-U+U.+Ixfa8M(x)M.(x) dxL-J 44图cEI
§11–2 莫尔定理(单位力法) C A U =U+U +1f 0 = L x EI M x U d 2 ( ) 2 = L x EI M x U d 2 ( ) 2 0 0 + = L C x EI M x M x U d 2 [ ( ) ( )]2 0 = L A x EI M x M x f d ( ) ( ) 0 求任意点A的位移f A 。 一、定理的证明: a A 图 fA q(x) 图c A P0 =1 q(x) f A 图b A P0=1

能量方法 M(x)M.()dx莫尔定理(单位力法)二EI一、普遍形式的莫尔定理.-I N(N()ax+J M(M(a+ I M()M()ax1EIEAGI
莫尔定理(单位力法) 二、普遍形式的莫尔定理 x EI M x M x f L A d ( ) ( ) 0 = = + + L P n n L A x GI M x M x x EA N x N x d ( ) ( ) d ( ) ( ) 0 0 x EI M x M x L d ( ) ( ) 0