西安电子科技大学：《神经网络与模糊系统 Neural Networks and Fuzzy Systems》课程PPT课件讲稿（2006）Chapter 03-2 NEURONAL DYNAMICS 2：ACTIVATION MODELS

Bivalent BAM theorem △S,(x)=1-0=1△S,(x;)=0-1=-1 For bipolar threshold signal functions AS,(x)=2 AS,(x;)=-2 The“energy'change△L △L=Lk+1-Lk Differs from zero because of changes in field Fy or in field Fy 7

7 Bivalent BAM theorem Si (xi ) = 1− 0 = 1  ( ) = 0 −1 = −1 i i S x Si (xi ) = 2 Si (xi ) = −2 For bipolar threshold signal functions The “energy”change L L = Lk+1 − Lk Differs from zero because of changes in field or in field FX FY

Bivalent BAM theorem △L=-△S(X)MS(Yk)'-△S(X)[I-U] =-AS(X)IS(Y)M-U =-∑∑AS,(,)S,0y)m∑AS,(x)山，+∑AS,(x,U -∑As,(G∑S0ym,-∑aSx川，+∑As, =-∑AS,(x)∑S,)m,+1,-U] =-AS,(x,Ix41-U月 8

8 Bivalent BAM theorem T T L = −S(X)MS(Yk ) − S(X) [I −U] T T = −S(X)[S(Yk )M −[I −U]] = − − + i i i i i i i i i j i j k T Si xi S j y m S x I S x U j ( ) ( ) ( ) ( ) = −  − + i i i i i i i i i j i j k T Si xi S j y m S x I S x U j ( ) ( ) ( ) ( ) ( )[ ( ) ] i i i j i j k T Si xi S j y m I U j = −  + − ( )[ ]i i k = −Si xi xi −U +1  0

Bivalent BAM theorem Suppose AS;(x;)>0 Then AS;(x)=S;()-S;(x) =1-0 This implies so the product is positive: △S,(x,)[x+1-U,]>0 Another case suppose AS;(x;)<0 △S,(x)=S,(x,k+1)-S,(x,) =0-1 9

9 Bivalent BAM theorem Suppose Si (xi )  0 ( ) ( ) ( ) k i i k i i i i S x = S x − S x +1 = 1− 0 Then This implies so the product is positive: i k xi U +1 0 1  −  + ( )[ ] i k Si xi xi U Another case suppose Si (xi )  0 ( ) ( ) ( ) k i i k i i i i S x = S x − S x +1 = 0 −1

Bivalent BAM theorem -This impliesxUs so the product is positive: AS,(x)[x+1-U,>0 So+-Lk<0 for every state change. -Since L is bounded,L behaves as a Lyapunov function for the additive BAM dynamical system defined by before. Since the matrix M was arbitrary,every matrix is bidirectionally stable.The bivalent BAM theorem is proved. 10

10 Bivalent BAM theorem This implies so the product is positive: i k xi U +1 0 1  −  + ( )[ ] i k Si xi xi U So for every state change. 0 Lk+1 − Lk  Since L is bounded,L behaves as a Lyapunov function for the additive BAM dynamical system defined by before. Since the matrix M was arbitrary,every matrix is bidirectionally stable. The bivalent BAM theorem is proved

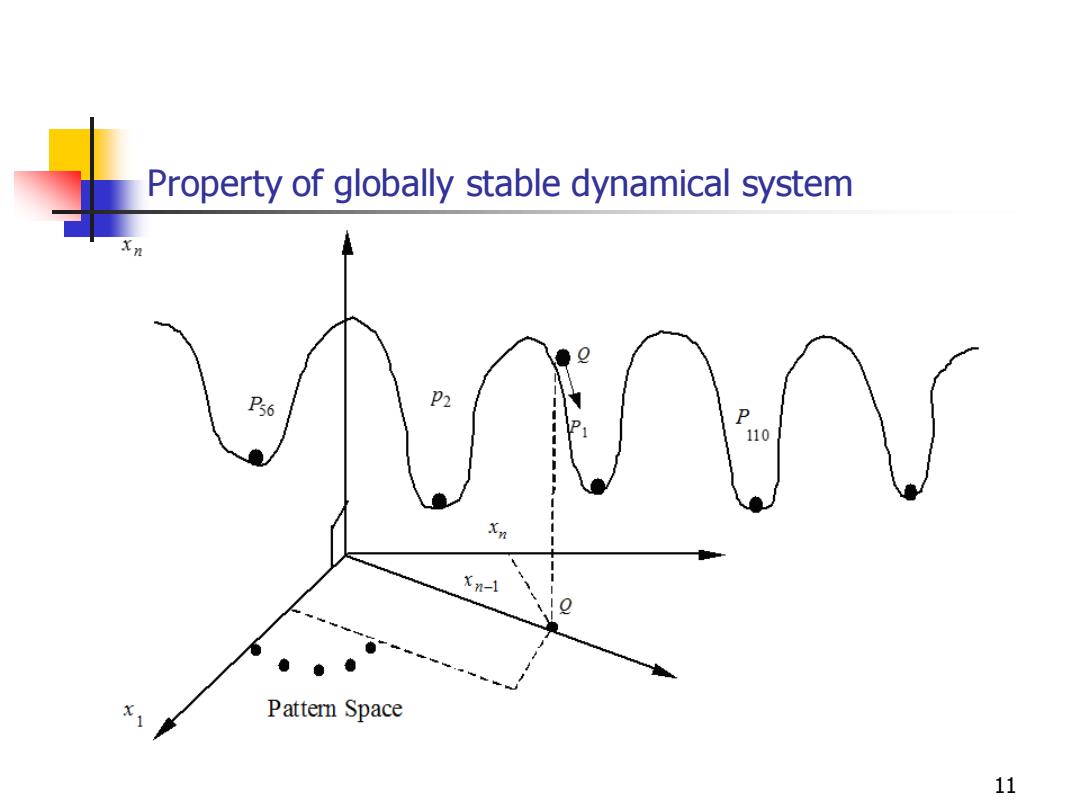
Property of globally stable dynamical system 56 P2 110 Xn-1 Pattern Space 11

11 Property of globally stable dynamical system