
当△V→0,取△P△的极限,就得出导体内任一点的热功 率密度,表示为 △P p=lim =EJ=0E? AV→0△V 或 p=J·E 此式就是焦耳定律的微分形式。 应该指出,焦耳定律不适应于运流电流。因为对于运流电 流而言,电场力对电荷所作的功转变为电荷的动能,而不 是转变为电荷与晶格碰撞的热能
当ΔV→0,取ΔP/ΔV的极限,就得出导体内任一点的热功 率密度,表示为 2 0 lim EJ E V P p V = = = → 或 p = J E 此式就是焦耳定律的微分形式。 应该指出,焦耳定律不适应于运流电流。因为对于运流电 流而言,电场力对电荷所作的功转变为电荷的动能,而不 是转变为电荷与晶格碰撞的热能

3.1.2恒定电流场的基本方程 电荷守恒定律 =路-wr s=0 要使积分对任意的体积均成立,必须使被积函数为零,即 口.j+p=0 a 2=0 8t 8 7.j=0 f7-a=0
电荷守恒定律 = − = − S V dV dt d dt dq J dS dV t J dS S V = − = 0 + dV t J V 要使积分对任意的体积V均成立,必须使被积函数为零,即 = 0 + t J = 0 t J = 0 = S J dS 0 3.1.2 恒定电流场的基本方程

电源外部导体中恒定电场的基本方程归纳如下: 7.j=0 7×E=0 与其相应的积分形式为 fJ.ds=0 fE-di=0
0 0 = = E J = = l S E dl J dS 0 0 电源外部导体中恒定电场的基本方程归纳如下: 与其相应的积分形式为

电流密度J与电场强度E之间满足欧姆定律J=σE。 以上的电场是指库仑场,因为在电源外的导体中,非库仑 场为零。 因恒定电场的旋度为零,因而可以引入电位0,E--。在 均匀导体内部(电导率6为常数),有 V.E=V.(-70)=-V0=0
电流密度J与电场强度E之间满足欧姆定律J=σE。 以上的电场是指库仑场, 因为在电源外的导体中, 非库仑 场为零。 因恒定电场的旋度为零,因而可以引入电位φ, E= -▽φ。 在 均匀导体内部(电导率σ为常数),有 ( ) 0 2 E = − = − =
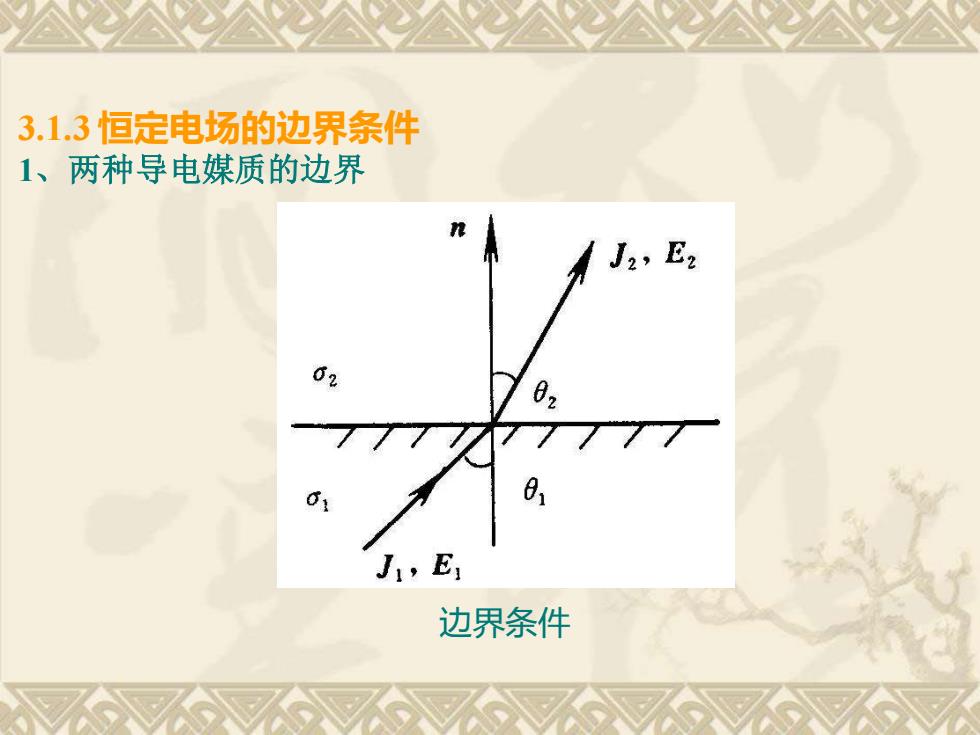
3.1.3恒定电场的边界条件 1、两种导电媒质的边界 J2,E2 02 1,E1 边界条件
3.1.3 恒定电场的边界条件 1、两种导电媒质的边界 边界条件