
第四章 静态场的解 已知,电位0与电场强度E的关系为 E=-70 对上式两边取散度,得 7.E=-V20 对于线性各向同性的均匀介质,电场强度E的散度为 V.E=P 那么,线性各向同性的均匀介质中,电位满足的微分方程式为 720=- 该方程称为泊松方程。 对于无源区,上式变为 720=0 上式称为拉普拉斯方程
已知,电位 与电场强度 E 的关系为 对上式两边取散度,得 对于线性各向同性的均匀介质,电场强度 E 的散度为 E = − 2 E = − E = 那么,线性各向同性的均匀介质中,电位满足的微分方程式为 = − 2 该方程称为泊松方程。 对于无源区,上式变为 0 2 = 上式称为拉普拉斯方程。 第四章 静态场的解

4.1边值问题的分类 确定积分常数) 边值问题是指存在边界面的电磁问题。 根据给定边界条件对边值问题分类: 第一类边值问题:已知电位函数在全部边界面上的分布值。 pL、=f 第二类边值问题:已知函数在全部边界面上的法向导数。 第三类边值问题(混合边值问题):已知一部分边界面上的函 数值,和另一部分边界面上函数的法向导数。 00 S=
4.1 边值问题的分类 边值问题是指存在边界面的电磁问题。 根据给定边界条件对边值问题分类: 第一类边值问题:已知电位函数在全部边界面上的分布值。 第二类边值问题:已知函数在全部边界面上的法向导数。 S = f S f n = 2 2 S f n = 第三类边值问题(混合边值问题):已知一部分边界面上的函 数值,和另一部分边界面上函数的法向导数。 1 S 1 = f 1 2 S S S = + (确定积分常数)
例1:已知无限长同轴电缆内、外半径分别为R和R2,如图所 示,电缆中填充均匀介质,内外导体间的电位差为U, 外导体接地。求其间各点的电位和电场强度。 解:根据轴对称的特点和无限长的假设, 可确定电位函数满足一维拉普拉斯方程, 采用圆柱坐标系 L0(r⊙单)=0积分中=AInr+B r arar U=AlnR+B、A= U U B=- -In R2 由边界条件 0=4InR,+B In R In R U 则:中= 龙= In E=-Vφ R e R
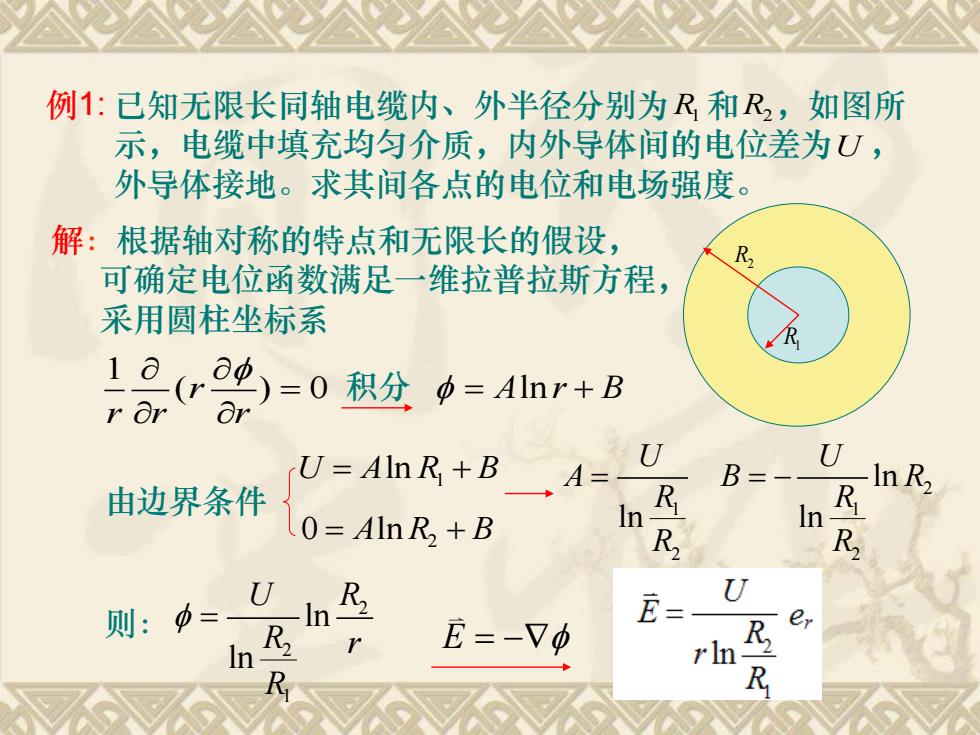
R2 R1 例1: 已知无限长同轴电缆内、外半径分别为 和 ,如图所 示,电缆中填充均匀介质,内外导体间的电位差为 , 外导体接地。求其间各点的电位和电场强度。 R1 R2 U 解:根据轴对称的特点和无限长的假设, 可确定电位函数满足一维拉普拉斯方程, 采用圆柱坐标系 1 ( ) 0 r r r r = 积分 = + A r B ln 由边界条件 1 U A R B = + ln 2 0 ln = + A R B 2 1 1 2 2 ln ln ln U U A B R R R R R = = − 2 2 1 ln ln U R R r R 则: = E = −

例2设一段环形导电媒质,其形状及尺寸如图示。计算两个端面 之间的电阻。 解显然,必须选用圆柱坐标系。设两 个端面之间的电位差为U,且令 当角度中时,电位g=0 0 当角度0=的,电位%=U 那么,由于导电媒质中的电位”仅与角度中有关,因此电位满足 的方程式为 do do2 ≥0 此式的通解为 p=C10+C2
例2 设一段环形导电媒质,其形状及尺寸如图示。计算两个端面 之间的电阻。 U y x t a b r 0 (r,) 0 解 显然,必须选用圆柱坐标系。设两 个端面之间的电位差为U,且令 当角度 = 时,电位 0 。 1 = 0 当角度 时,电位 。 2 = 2 =U 那么,由于导电媒质中的电位 仅与角度 有关,因此电位满足 的方程式为 0 d d 2 2 = 此式的通解为 =C1 + C2

利用给定的边界条件,求得 2U "2型 0= π 导电媒质中的电流密度J为 J=0E=-oVo=-eso ap 20U rod 0 那么由少=了的端面流进该导电媒质的电流/为 1-as〔e2 (-edr 电流密度矢量 因此该导电块的两个端面之间的电阻R为 U π R= b a
利用给定的边界条件,求得 2U = r U r 2 J E e = −e = = − = − 导电媒质中的电流密度J 为 那么由 的端面流进该导电媒质的电流 I 为 2 = ( d ) π 2 d t r r U I S J S e e S − = = − = = a Ut b r Ut b r a ln π d 2 π 2 因此该导电块的两个端面之间的电阻R 为 = = a b t I U R 2 ln π 电流密度矢量