
综合实验 实验41霍尔位置传感器法测量杨氏模量 一、实验目的 1.学习用梁弯曲法测定金属的杨氏模量值: 2.研究梁的弯曲程度与梁的长度、宽度、厚度、负重等之向间的关系。 3.学握基本长度和微小位移量测量的新方法和手段: 4.弯曲法测量金属板材的杨氏模量,对霍尔位骨传感器定标: 5。测量可锻铁的杨氏棋量。 二、实验原理 1879年,美国物理学家霍尔(Edwin Herbert Hall,.1855一1938)发现,当电流/垂直 于外磁场B的方向流过某导电体时,在垂直于电流和磁场的方向,该导电体的两侧会产生电 势差UH,它的大小与I和B的乘积成正比,而与导电 体沿磁场方向的厚度d成反比。这一现象被称为霍尔效 应。一般来说,金属和电解质的霍尔效应较小,半导体 的霍尔效应较显著,霍尔效应的数学表达式为 out U =RIB/d=KIB (1) 式中R为导电体的霍尔系数,K人称为元件的霍尔灵 敏度。如果保持霍尔元件的电流1不变,而使其在一个 图1霍尔位置传感器 均匀梯度的磁场中沿梯度方法移动时,则输出的霍尔电 势差变化量为 A0,=N2 (2) 式中△Z为位移量。此式说明在一个均匀梯度的磁场中,△U,与△Z成正比。 为实现均匀梯度的磁场,可如图1所示选用两块相同的磁铁(磁铁截面积及表面磁感应 强度相同),并使N极与N极相对而放置,两磁铁之间留一等间距间隙,霍尔元件平行于磁 铁放在该间隙的中轴上。间碟大小要根据测量范围和测量灵敏度要求而定,间隙越小,磁场 梯度就越大,灵敏度就越高。磁铁截面积要远大于霍尔元件的面积,以尽可能地减小边缘效 应影啊,提高测量准确度。 山于磁铁间隙内中心截面A处的磁感应强为零,霍尔元件处于该处时,输出的霍尔电 势差应为零。当霍尔元件偏离中心,沿乙发生位移时,山于磁感应强度不再为零,霍尔元

件就产生相应的电势差输出,其大小可山数学电压表测量。山此可以将霍尔电势差为零时元 件所处的位胃作为位移参考零点。 霍尔电势差与位移量之间存在一一对应关系,当位移量较小时(<2m)这一对应关 系具有良好的线性。在横梁弯曲情况下,杨氏模量E用下式表示 E=d'mg (3) 4a'b△Z 其中,d为两刀口间的距离,a为梁的厚度,b为梁的宽度,m为加挂砝码的质量,△☑ 为梁中心山于外力作用而下降的距离,g为重力加速度 三、实验仪器及介绍 梁弯曲实验仪(含读数显微镜、95A型集成霍尔位置传感器、磁铁两块、带刀口的可调 实数显微 FD-HY-1 杨氏模量实验仪 图2杨氏模量仪器实物图 支座、带刀口的金属框、砝码、水半仪等)如图2所示、米尺,游标卡尺,螺旋测微器,砝 码,待测材料(一根黄铜、一根可转锻铁)。 四、实验内容与步骤 1.将待测梁放在两支座上端的刀口上,套上金属框并使刀刃好在仪器两刀口的中间 2.水准泡放在梁上,用支座下底可调底脚调节,直全梁处于水平位置。 3.调节读数测量显微镜的上下和无右位置,使镜筒轴线正对金属框上的小园孔。调节 显微镜目镜,使之看清楚镜筒内的丨宁线。前后移动显微镜,直到从镜中清渐看到棒的边缘, 耳进行微调,使显微镜的宁线与梁的某一边缘重合无视差。这时,从显微镜上读出其位置。 4.杨氏模量的测量和霍尔位传感器的定标 将一根黄铜架好,调整好测微目镜,逐步加上一定量的砝码,使梁弯曲产尘位移△☑: 精确测量传感器信号输出端的数值并用测微目镜测量固定砝码架的位置Z,记录毫伏表的读
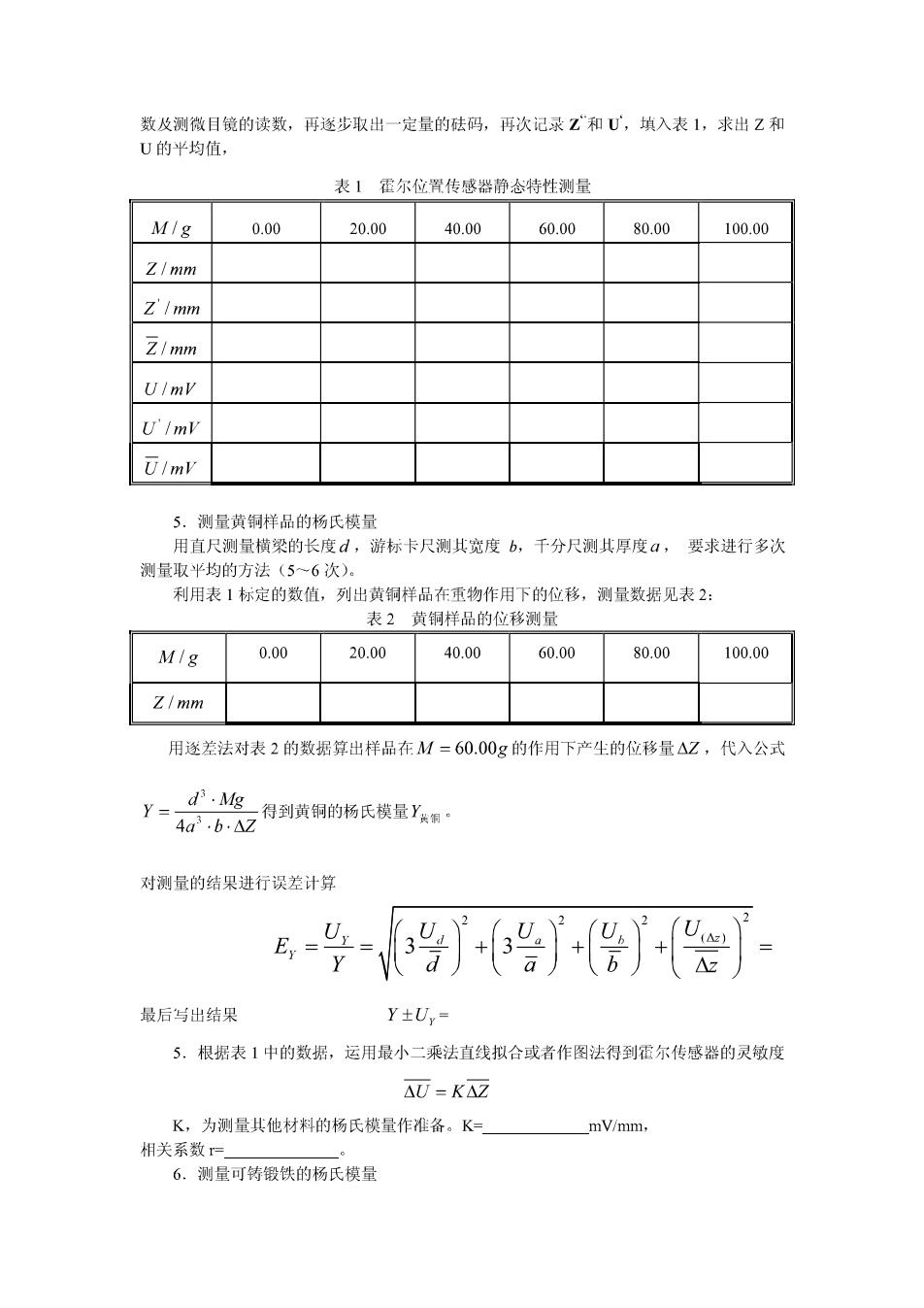
数及测微日镜的读数,再逐步取出一定量的砝码,再次记录Z和U,填入表1,求出Z和 U的华均值, 表【霍尔位置传感器静态特性测量 0.00 20.00 40.00 60.0080.00100.00 Z/mm Zimm 乙/mm UlmV U/mV UlmV 5.测量黄铜样品的杨氏模量 用直尺测量横梁的长度d,游标卡尺测其宽度b,千分尺测其厚度a,要求进行多次 测量取平均的方法(5一6次 利用表1标定的数值, 列出黄铜样品在重物作用下的位移,测量数据见表2 表2黄铜样品的位移测量 Mig 0.00 20.00 40.00 60.0080.00100.00 用逐差法对表2的数据算出样品在M=60.00g的作用下产生的位移量△Z,代入公式 Y 406,A2得到黄钢的6氏模量X4 d.Mg 对测量的结果进行误差计算 Ey= U 最后写出结果 Y±U,= 5.根据表1中的数据,运用最小二乘法直线拟合或者作图法得到霍尔传感器的灵敏度 AU=K△Z K,为测量其他材料的杨氏模量作准备。K= mV/mm 相关系数 6.测量可铸锻铁的杨氏模量
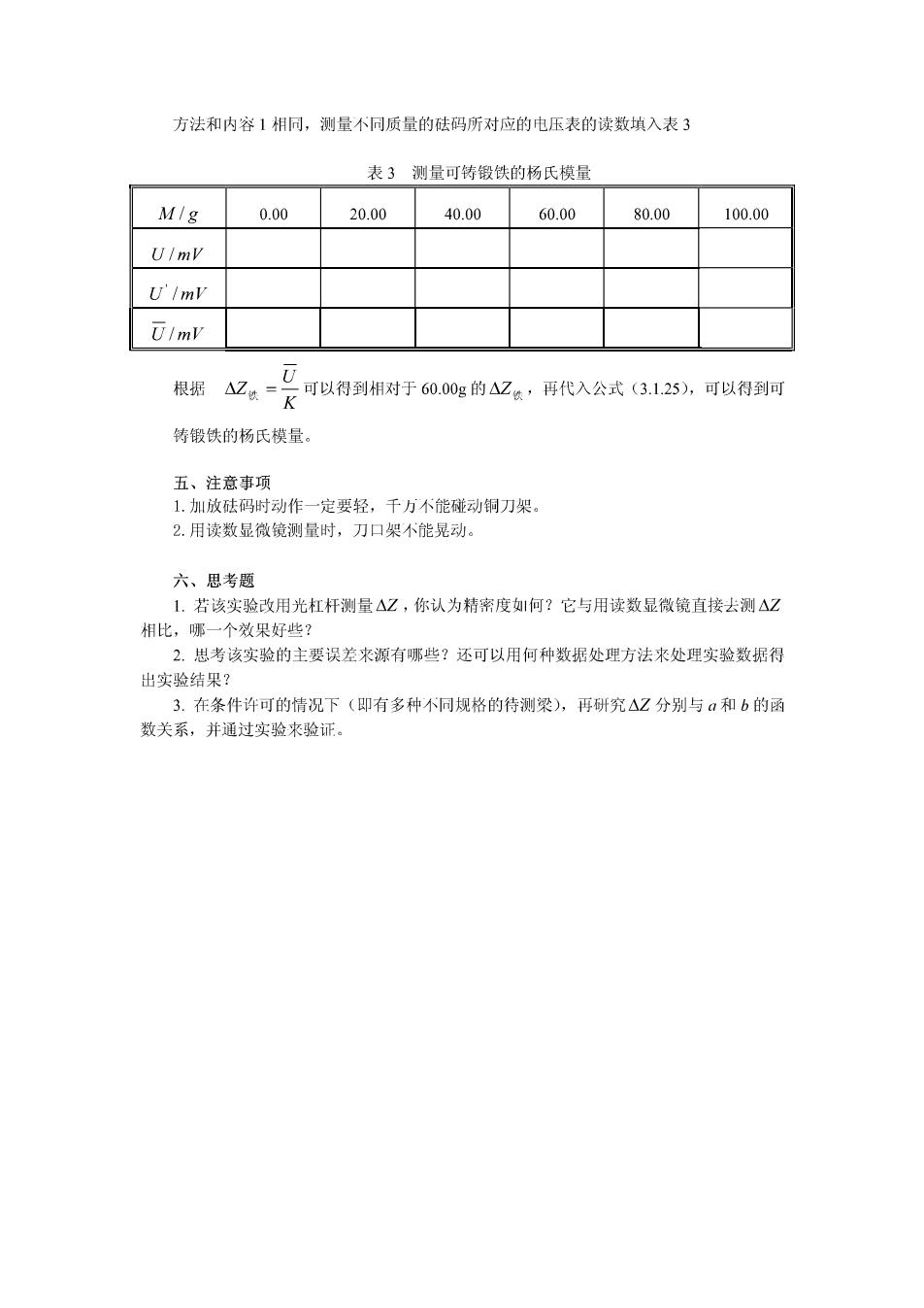
方法和内容1相同,测量不洞质量的砝码所对应的电压表的读数填入表3 表3测量可特锻铁的杨氏模量 M/g 0.0020.00 40.00 60.00 80.00100.00 UlmV UlmV 元1mV 根据口。一又可以得到相对于00g的山。,得代入公式(3125》,可以利时 铸锻铁的杨氏模量。 五、注意事项 1.加放砝码时动作 一定要轻,千力不能碰动铜刀架 2.用读数显微镜测量时,刀口架不能晃动。 六、思考题 1.若该实验改用光杠杆测量△Z,你认为精来度如何?它与用读数显微镜直接去测△Z 相比,哪一个效果好些? 2.思考该实验的主要误差来源有哪些?还可以用何种数据处理方法来处理实验数据得 出实验结果? 3.在条件许可的情况下(即有多种不同规格的待测梁),再研究△Z分别与和b的函 数关系,并通过实验来验证

实验42热敏电阻温度特性的研究(非平衡电桥的使用) 一、实验目的 1.研究负电阻温度系数(热敏电阻)的温度特性: 2。堂辉非业衡电侨的原甲及定标方法 3.学习线形拟合法处理数据 实验原理 1.负温度系数半导体热敏电阻的温度特性 山半导体能带结构可知,它是禁带宽度E,较小(一般在1ev一2ev左右)的固体,电子很 容易从价带(满带)激发企导带,同时价带中产生空穴,这就是所谓的本征激发,这类半导 体通常称本征半导体(无杂质和缺陷的半导体).高纯度的半导体和较高温度的半导体也具 有本征半导体的性质。统计理论指出,山于热激发导带中的电子浓度随 高而呈指数 地增加,而本征半导体的电阻率(或电导率)与温度的关系主要取决于电子浓度同温度的关 系,因此,半导体热敏电阻可表示为 R,=Ae=Ae (1) 其中Rr是热力学温度为T时的电阻值,R是热力学温度为T时的电阻值,在常温或较高温 度下B是正比于禁带宽度E的常数,只与材料的性质有关,B=E,k,k为玻耳兹曼常数 A是与热敏电阳的尺」及材料性质有关的常量。上式取对数可化为 hR=a4+号 (2) 山此可知nR,与二成线性关系,只要测出 R 不同温度T以及相对应的R值,通过式(1)进 行线性拟合,即可求得表征热敏电阻温度特征的 常数B、A,进而估算禁带宽度E,常用的热敏 电阻的B值约为1500K一5000K, 2.非平衡桥 惠斯通电桥工作在平衡状念下,即桥臂上的 电阻是处在稳定状态下,其阻值不随环境的变化 网1流电桥电 而变化。如图1,平衡时毫伏表输出为零,有 3 而非半衡电桥,顾名思义,就是电桥工作在非半衡状态,桥臂上的电阻随若环境的变化 而变化,温位、湿度、压力、光福等。由桥中的一个成一个以上的侨,往往是且右一 定功能的变换元件,如压电传感器,热敏传感器,湿度传感器等等。这些元件的电阻值可以 随某一物理量的变化而变化:这样就可以通过测量功能元件阻值的变化来测定有关物理量的 变化量,山此制成一些测量仪表,比电子科、真空计、温度计等。 设某一状态下桥处于平衡,为简单计,我们假定桥臂电阻R,R,R;是固定的,只考 虑一个电阻R,是变化的,并且该电阻就是我们研究的热敏电阻,此时温度为,BD两端的 电压Uo为