
《电磁场与电磁波》试题1 一、填空题(每小题1分,共10分) 1.在均匀各向同性线性媒质中,设媒质的导磁率为“,则磁感应强度B和磁场户满足的 方程为: 2.设线性各向同性的均匀媒质中,V中=0称为 方程。 3.时变电磁场中,数学表达式S=E×H称为」 4.在理想导体的表面, 一的切向分量等于零。 5.失量场A()穿过闭合曲面S的通量的表达式为: 6.电磁波从一种媒质入射到理想 一表面时,电磁波将发生全反射。 7.静电场是无旋场,故电场强度沿任一条闭合路径的积分等于 8.如果两个不等于零的矢量的 等于零,则此两个矢量必然相互垂直。 9.对平面电磁波而言,其电场、磁场和波的传播方向三者符合 关系。 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 数的旋度来表示。 二、简述题(每小题5分,共20分) 11.已知麦克斯韦第二方程为】 ×E=- 动,试说明其物理意义,并写出方程的积分形式。 12.试简述唯一性定理,并说明其意义。 13.什么是群速?试写出群速与相速之间的关系式。 14.写出位移电流的表达式,它的提出有何意义? 三、计算题(每小题10分,共30分) 15.按要求完成下列题目 (D判斯矢最函数B=-少,+,是香是某区域的通量密度 (2)如果是,求相应的电流分布。 16.矢量4=22,+6,-39,B=56,-3,-6,求 (1)A+B (2)AB 17,在无源的自由空间中,电场强度复矢量的表达式为 E=e3E。-e,4E-k
《电磁场与电磁波》试题 1 一、填空题(每小题 1 分,共 10 分) 1.在均匀各向同性线性媒质中,设媒质的导磁率为 ,则磁感应强度 B 和磁场 H 满足的 方程为: 。 2.设线性各向同性的均匀媒质中, 0 2 = 称为 方程。 3.时变电磁场中,数学表达式 S E H = 称为 。 4.在理想导体的表面, 的切向分量等于零。 5.矢量场 A(r) 穿过闭合曲面 S 的通量的表达式为: 。 6.电磁波从一种媒质入射到理想 表面时,电磁波将发生全反射。 7.静电场是无旋场,故电场强度沿任一条闭合路径的积分等于 。 8.如果两个不等于零的矢量的 等于零,则此两个矢量必然相互垂直。 9.对平面电磁波而言,其电场、磁场和波的传播方向三者符合 关系。 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 函 数的旋度来表示。 二、简述题 (每小题 5 分,共 20 分) 11.已知麦克斯韦第二方程为 t B E = − ,试说明其物理意义,并写出方程的积分形式。 12.试简述唯一性定理,并说明其意义。 13.什么是群速?试写出群速与相速之间的关系式。 14.写出位移电流的表达式,它的提出有何意义? 三、计算题 (每小题 10 分,共 30 分) 15.按要求完成下列题目 (1)判断矢量函数 x y B y e ˆ xze ˆ 2 = − + 是否是某区域的磁通量密度? (2)如果是,求相应的电流分布。 16.矢量 x y z A = 2e ˆ + e ˆ −3e ˆ , x y z B = 5e ˆ − 3e ˆ − e ˆ ,求 (1) A B + (2) A B 17.在无源的自由空间中,电场强度复矢量的表达式为 ( ) jkz x y E e E e E e − = 0 − 4 0 ˆ 3 ˆ
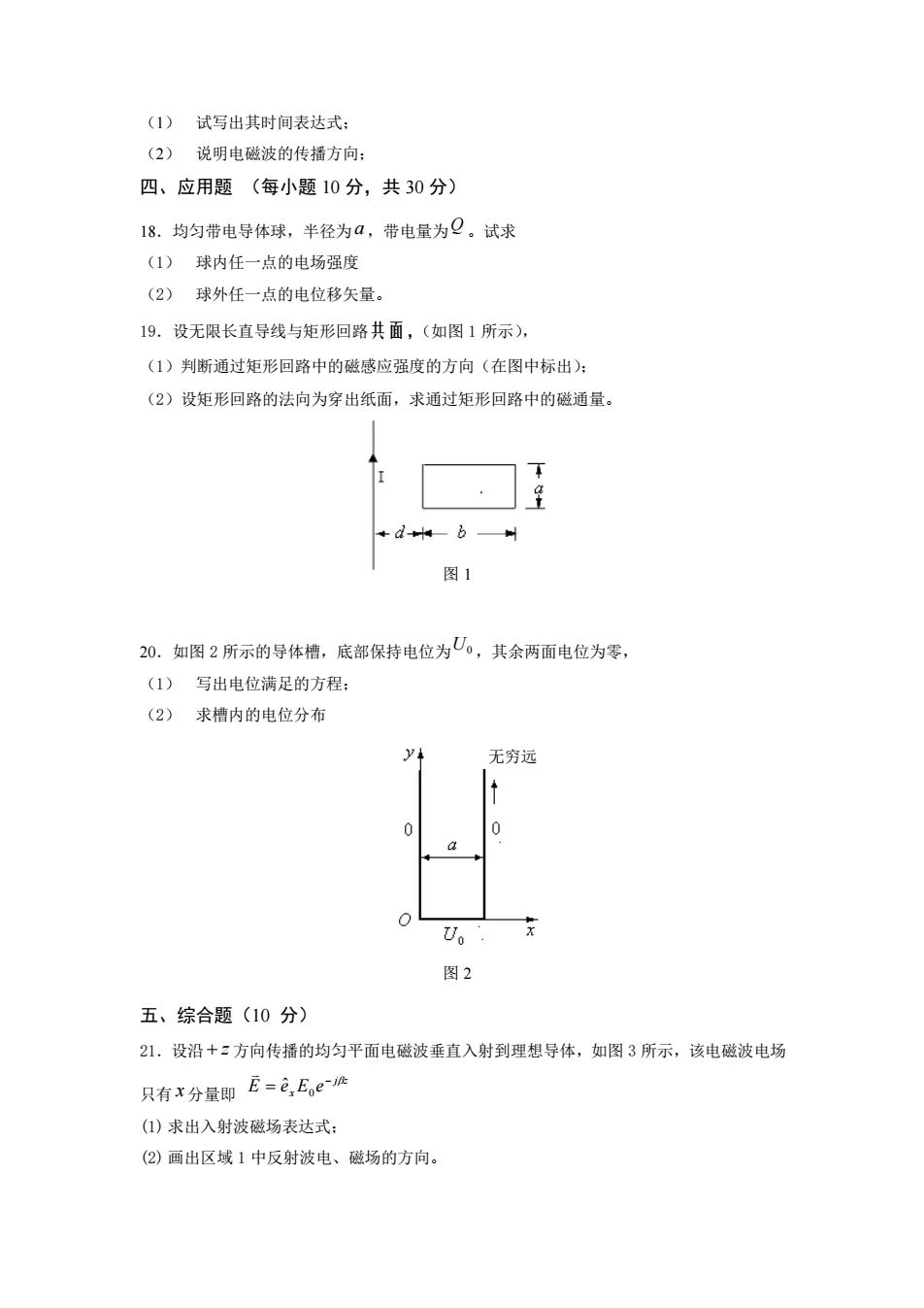
(1)试写出其时间表达式: (2)说明电磁波的传播方向: 四、应用题(每小题10分,共30分) 18.均匀带电导体球,半径为a,带电量为Q。试求 (1)球内任一点的电场强度 (2)球外任一点的电位移矢量。 19.设无限长直导线与矩形回路共面,(如图1所示), (1)判断通过矩形回路中的磁感应强度的方向(在图中标出): (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。 +d中b州 图1 20.如图2所示的导体槽,底部保持电位为U0,其余两面电位为零, (1)写出电位满足的方程 (2)求槽内的电位分布 y 无穷远 U。 图2 五、综合题(10分) 21.设沿+方向传播的均匀平面电磁波垂直入射到理想导体,如图3所示,该电磁波电场 只有x分量即E=色E。e ()求出入射波磁场表达式: (②)画出区域1中反射波电、磁场的方向
(1) 试写出其时间表达式; (2) 说明电磁波的传播方向; 四、应用题 (每小题 10 分,共 30 分) 18.均匀带电导体球,半径为 a ,带电量为 Q 。试求 (1) 球内任一点的电场强度 (2) 球外任一点的电位移矢量。 19.设无限长直导线与矩形回路共面,(如图 1 所示), (1)判断通过矩形回路中的磁感应强度的方向(在图中标出); (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。 20.如图 2 所示的导体槽,底部保持电位为 U0 ,其余两面电位为零, (1) 写出电位满足的方程; (2) 求槽内的电位分布 五、综合题(10 分) 21.设沿 + z 方向传播的均匀平面电磁波垂直入射到理想导体,如图 3 所示,该电磁波电场 只有 x 分量即 j z x E e E e − = 0 ˆ (1) 求出入射波磁场表达式; (2) 画出区域 1 中反射波电、磁场的方向。 无穷远 图 2 图 1

4, 理想导体 区域1 区域2 图3 《电磁场与电磁波》试题2 一、填空题(每小题1分,共10分) 1在均匀各向同性线性媒质中,设媒质的介电常数为,则电位移矢量D和电场E满足的 方程为: 2.设线性各向同性的均匀媒质中电位为中,媒质的介电常数为5,电荷体密度为P,电位 所满足的方程为 3.时变电磁场中,坡印廷矢量的数学表达式为 4.在理想导体的表面,电场强度的 分量等于零。 ∮Ad 5.表达 称为矢量场4(F)穿过闭合曲面S的 6。电磁波从一种媒质入射到理想导体表面时,电磁波将发生 7.静电场是保守场,故电场强度沿任一条闭合路径的积分等于 8.如果两个不等于零的矢量的点积等于零,则此两个矢量必然相互 9.对横电磁波而言,在波的传播方向上电场、磁场分量为 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是_ _场,因此,它可用磁矢 位函数的旋度来表示。 二、简述题(每小题5分,共20分) 11.试简述磁通连续性原理,并写出其数学表达式。 12.简述亥姆霍兹定理,并说明其意义。 fE.di=-onds 13.己知麦克斯韦第二方程为 试说明其物理意义,并写出方程的微 分形式。 14.什么是电磁波的极化?极化分为哪三种? 三、计算题(每小题10分,共30分)
《电磁场与电磁波》试题 2 一、填空题(每小题 1 分,共 10 分) 1.在均匀各向同性线性媒质中,设媒质的介电常数为 ,则电位移矢量 D 和电场 E 满足的 方程为: 。 2.设线性各向同性的均匀媒质中电位为 ,媒质的介电常数为 ,电荷体密度为 V ,电位 所满足的方程为 。 3.时变电磁场中,坡印廷矢量的数学表达式为 。 4.在理想导体的表面,电场强度的 分量等于零。 5.表达式 A(r) dS S 称为矢量场 A(r) 穿过闭合曲面 S 的 。 6.电磁波从一种媒质入射到理想导体表面时,电磁波将发生 。 7.静电场是保守场,故电场强度沿任一条闭合路径的积分等于 。 8.如果两个不等于零的矢量的点积等于零,则此两个矢量必然相互 。 9.对横电磁波而言,在波的传播方向上电场、磁场分量为 。 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是 场,因此,它可用磁矢 位函数的旋度来表示。 二、简述题 (每小题 5 分,共 20 分) 11.试简述磁通连续性原理,并写出其数学表达式。 12.简述亥姆霍兹定理,并说明其意义。 13.已知麦克斯韦第二方程为 dS t B E dl C S = − ,试说明其物理意义,并写出方程的微 分形式。 14.什么是电磁波的极化?极化分为哪三种? 三、计算题 (每小题 10 分,共 30 分) 区域 1 区域 2 图 3

15.矢量函数A=-x.+ze.n (1)V.A (2)V×A 16.矢量4=22,-2,B=6,-,求 (1)A-B (2)求出两矢量的夹角 17.方程化,火)=x2+少2+:子给出一球族,求 (1)求该标量场的梯度: (2)求出通过点12,0)处的单位法向矢量 四、应用题(每小题10分,共30分) 18.放在坐标原点的点电荷在空间任一点F处产生的电场强度表达式为 E=48, (1)求出电力线方程:(2)画出电力线。 19.设点电荷位于金属直角劈上方,如图1所示,求 (1)画出镜像电荷所在的位置 (2)直角劈内任意一点(,八)处的电位表达式 ·(xy,z) ·9(1,2,0) 图1 20.设时变电磁场的电场强度和磁场强度分别为: E-E。cos(ct-4) i=H。cos(ol-pm) (1)写出电场强度和磁场强度的复数表达式 (2)证明其坡印廷矢量的平均值为: 5-,×i,o- 五、综合题(10分) 21.设沿+:方向传播的均匀平面电磁波垂直入射到理想导体,如图2所示,该电磁波电场 只有x分量即E=色,Eem
15.矢量函数 x z A yx e ˆ yze ˆ 2 = − + ,试求 (1) A (2) A 16.矢量 x z A = 2e ˆ − 2e ˆ , x y B = e ˆ − e ˆ ,求 (1) A B − (2)求出两矢量的夹角 17.方程 2 2 2 u(x, y,z) = x + y + z 给出一球族,求 (1)求该标量场的梯度; (2)求出通过点 (1,2,0) 处的单位法向矢量。 四、应用题 (每小题 10 分,共 30 分) 18.放在坐标原点的点电荷在空间任一点 r 处产生的电场强度表达式为 r e r q E ˆ 4 2 0 = (1)求出电力线方程;(2)画出电力线。 19.设点电荷位于金属直角劈上方,如图 1 所示,求 (1) 画出镜像电荷所在的位置 (2) 直角劈内任意一点 (x, y,z) 处的电位表达式 20.设时变电磁场的电场强度和磁场强度分别为: cos( ) 0 e E = E t − cos( ) 0 m H = H t − (1) 写出电场强度和磁场强度的复数表达式 (2) 证明其坡印廷矢量的平均值为: cos( ) 2 1 Sav = E0 H0 e − m 五、综合题 (10 分) 21.设沿 + z 方向传播的均匀平面电磁波垂直入射到理想导体,如图 2 所示,该电磁波电场 只有 x 分量即 j z x E e E e − = 0 ˆ 图 1

(3)求出反射波电场的表达式: (④)求出区域1媒质的波阻抗。 , 理槭导体 区域1 区域2 图3 《电磁场与电磁波》试题3 一、填空题(每小题1分,共10分) 1.静电场中,在给定的边界条件下,拉普拉斯方程或 方程的解是唯一的,这一定理 称为唯一性定理。 2。在自由空间中电磁波的传播速度为 ms. 3.磁感应强度沿任一曲面S的积分称为穿过曲面S的 4.麦克斯韦方程是经典 理论的核心。 5.在无源区域中,变化的电场产生磁场,变化的磁场产生 ,使电磁场以波的形式 传播出去,即电磁波。 6.在导电媒质中,电磁波的传播速度随频率变化的现象称为 7.电磁场在两种不同媒质分界面上满足的方程称为 8。两个相互靠近、又相互绝缘的任意形状的_可以构成电容器。 9.电介质中的束缚电荷在外加电场作用下,完全脱离分子的内部束缚力时,我们把这种现 象称为 10.所谓分离变量法,就是将一个_ _函数表示成几个单变量函数乘积的方法。 二、简述题(每小题5分,共20分) 儿已知麦克断韦第一方程为x月=了,沙 ,试说明其物理意义,并写出方程的积分形 式。 12.试简述什么是均匀平面波。 13.试简述静电场的性质,并写出静电场的两个基本方程。 14.试写出泊松方程的表达式,并说明其意义。 三、计算题(每小题10分,共30分)
(3) 求出反射波电场的表达式; (4) 求出区域 1 媒质的波阻抗。 《电磁场与电磁波》试题 3 一、填空题(每小题 1 分,共 10 分) 1.静电场中,在给定的边界条件下,拉普拉斯方程或 方程的解是唯一的,这一定理 称为唯一性定理。 2.在自由空间中电磁波的传播速度为 m/s 。 3.磁感应强度沿任一曲面 S 的积分称为穿过曲面 S 的 。 4.麦克斯韦方程是经典 理论的核心。 5.在无源区域中,变化的电场产生磁场,变化的磁场产生 ,使电磁场以波的形式 传播出去,即电磁波。 6.在导电媒质中,电磁波的传播速度随频率变化的现象称为 。 7.电磁场在两种不同媒质分界面上满足的方程称为 。 8.两个相互靠近、又相互绝缘的任意形状的 可以构成电容器。 9.电介质中的束缚电荷在外加电场作用下,完全脱离分子的内部束缚力时,我们把这种现 象称为 。 10.所谓分离变量法,就是将一个 函数表示成几个单变量函数乘积的方法。 二、简述题 (每小题 5 分,共 20 分) 11.已知麦克斯韦第一方程为 t D H J = + ,试说明其物理意义,并写出方程的积分形 式。 12.试简述什么是均匀平面波。 13.试简述静电场的性质,并写出静电场的两个基本方程。 14.试写出泊松方程的表达式,并说明其意义。 三、计算题 (每小题 10 分,共 30 分) 区域 1 区域 2 图 2