Js=lim △ld -0△1dl =P, l=jJ,-idl=∫J,cosl △ 面电流密度
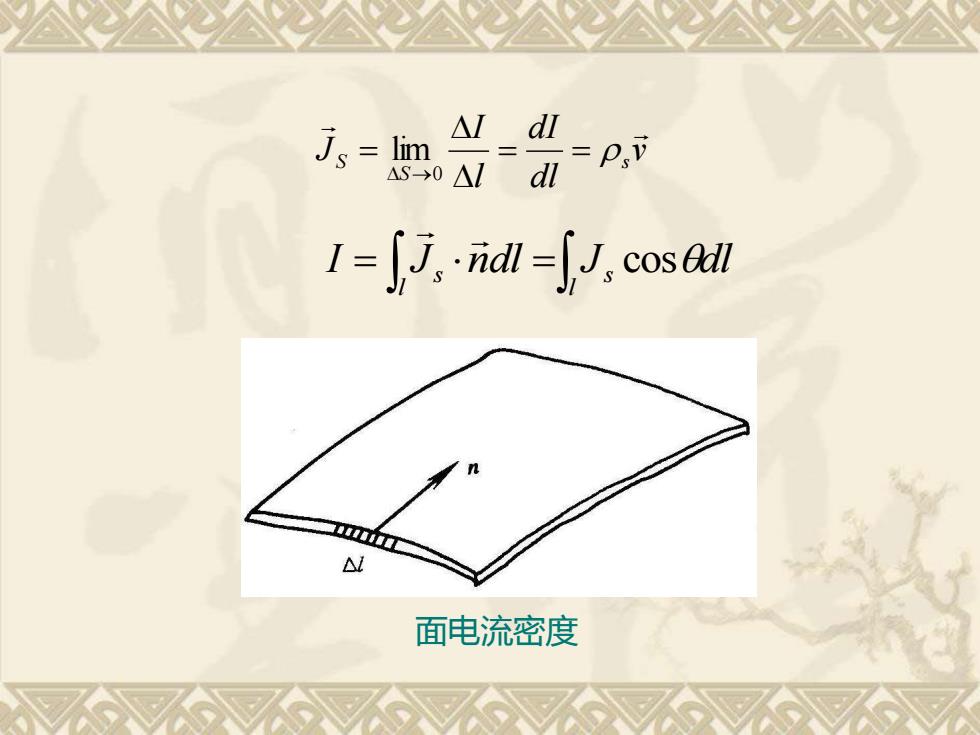
面电流密度 v dl dI l I J s S S = = = →0 lim = = l s l I Js ndl J cosdl

运流电流的电流密度并不与电场强度成正比,而且电流密度的 方向与电场强度的方向也可能不同。可以证明运流电流的电流密度 J与运动速度v的关系为 J=pv 式中p为电荷密度。 与介质的极化特性一样,媒质的导电性能也表现出均匀与非均匀, 线性与非线性以及各向同性与各同异性等特点,这些特性的含义与 前相同。上述公式仅适用于各向同性的线性媒质
运流电流的电流密度并不与电场强度成正比,而且电流密度的 方向与电场强度的方向也可能不同。可以证明运流电流的电流密度 J 与运动速度 v 的关系为 J v = 式中 为电荷密度。 与介质的极化特性一样,媒质的导电性能也表现出均匀与非均匀, 线性与非线性以及各向同性与各同异性等特点,这些特性的含义与 前相同。上述公式仅适用于各向同性的线性媒质

÷1、欧姆定律的微分形式 实验表明在导电媒质中,当温度不变时,媒质中某点的电流密 度J与该点的电场强度E成正比 j=o尼 欧姆定律的微分形式 由于电流密度可以视为单位面积的电流密度,电场强度可以 视为在电场强度方向单位长度上的电压。 因此,对一段长为1, 横截面为$的导线,欧姆定律的微分 形式可写成: 1=4U R σ值愈大表明导电能力 愈强,即使在微弱的 △I=JaS 电场作用下,也可形 △U=E△l >j=OE成很强的电流。 R= △l 电导率,单位:s/m O△S
❖ 1、欧姆定律的微分形式 由于电流密度可以视为单位面积的电流密度,电场强度可以 视为在电场强度方向单位长度上的电压。 因此,对一段长为 l ,横截面为S的导线,欧姆定律的微分 形式可写成: 实验表明在导电媒质中,当温度不变时,媒质中某点的电流密 度J 与该点的电场强度 E成正比 J E = 欧姆定律的微分形式 l s U I R I J s U E l l R s = = = = J E = 电导率, 单位:s/m 值愈大表明导电能力 愈强,即使在微弱的 电场作用下,也可形 成很强的电流
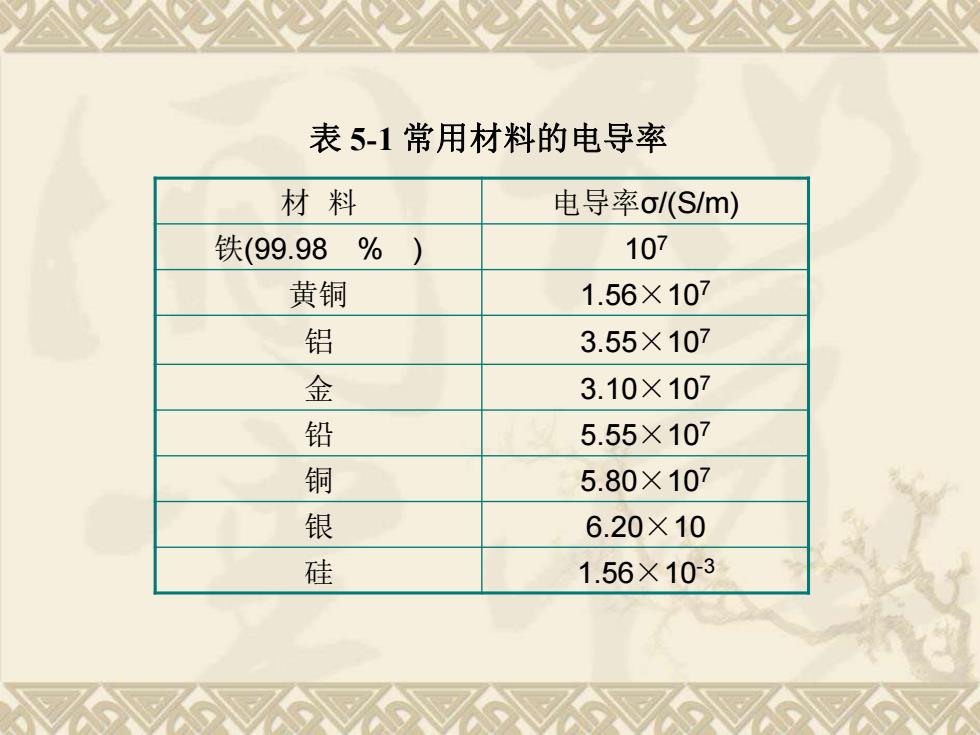
表5-1常用材料的电导率 材料 电导率o/(S/m) 铁(99.98%) 107 黄铜 1.56×107 铝 3.55×107 金 3.10×107 铅 5.55×107 铜 5.80×107 银 6.20×10 硅 1.56×103
材 料 电导率σ/(S/m) 铁(99.98 % ) 107 黄铜 1.56×107 铝 3.55×107 金 3.10×107 铅 5.55×107 铜 5.80×107 银 6.20×10 硅 1.56×10-3 表 5-1 常用材料的电导率

2、焦耳定律的微分形式 当导体两端的电压为U,流过的电流为时,则在单位时间 内电场力对电荷所作的功,即功率是 P=UI 在导体中,沿电流线方向取一长度为△1、截面为△S的体积 元,该体积元内消耗的功率为 △P=△J△I=E△M△I=EJ△l△S=EJ△/
2、 焦耳定律的微分形式 当导体两端的电压为U,流过的电流为I时,则在单位时间 内电场力对电荷所作的功,即功率是 P =UI 在导体中,沿电流线方向取一长度为Δl、截面为ΔS的体积 元,该体积元内消耗的功率为 P = UI = ElI = EJlS = EJV