s=a+a2+43+a4+d5 as d s Oaoo⊙8
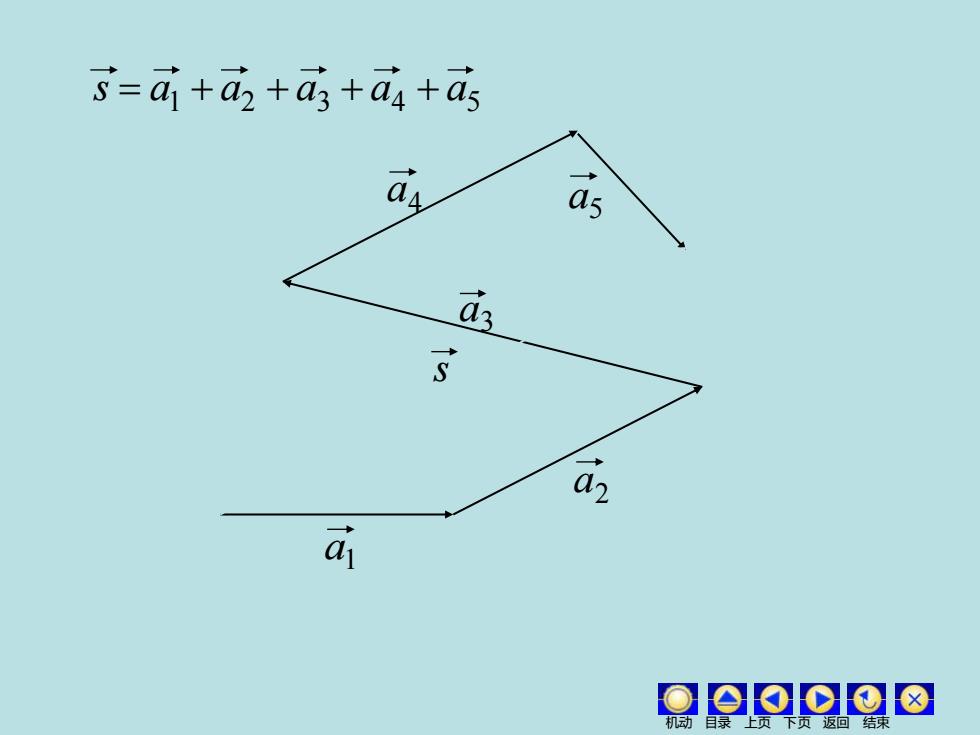
机动 目录 上页 下页 返回 结束 s a3 a4 a5 a2 a1 a1 a2 a3 a4 a5 s = + + + +

2.向量的减法 b-a-b+(-a) -a 6-d 特别当b=d时,有 b-a a-a=a+(-=d 三角不等式 atb s a+b a-b≤a+b OOo⊙o8
2. 向量的减法 三角不等式 机动 目录 上页 下页 返回 结束 a

3.向量与数的乘法 入是一个数,入与d的乘积是一个新向量,记作九. 规定:1>0时,a与a同向,2d=人d; <0时,a与a反向,九d=-d; 元=0时,a=0. 总之 Aa n a 运算律:结合律2(ud)=u(d)=九ud 分配律 (2+)a=元a+ud (a+b)=a+1b 若a#0,则有单位向量a=日a因此a=ad Oao⊙®8
a a = 3. 向量与数的乘法 是一个数 , a . 规定 : 1a a ; = 可见 1a a ; − = − 与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a) ( a) = a = 分配律 (a b) + a b = + = 则有单位向量 a . 1 a a 因此 a = a a 机动 目录 上页 下页 返回 结束

定理1.设为非零向量,则 a∥方一b=a(八为唯一实数) 证:“一”设a/6,取入=±石/a,d,6同向时 取正号,反向时取负号,则b与入同向,且 -哥8=网 故b=a. 再证数)的唯一性.设又有b=ua,则(2-w)a=0 而d≠0,故2-4=0,即九=4. Oao⊙⊙8
定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证: “ ”. , 取 =± 且 再证数 的唯一性 . 则 故 − = 0, 即 = . a∥b 设 a∥b 取正号, 反向时取负号, , a , b 同向时 则 b 与 a 同向, 设又有 b= a , ( − )a = 0 = = b 故 b = a. 机动 目录 上页 下页 返回 结束

一”已知=入d,则 当=0时,b=d 当1>0时,a,b同向 a∥b 当1<0时,a,b反向 例1.设M为□ABCD对角线的交点,AB=d,AD=b, 试用a与b表示MA,MB,MC,MD 解:a+b=AC=2MC=-2MA 6-a=BD=2MD=-2MB M :MA=-3(a+8)MB=-3(6-a) B MC=(a+b)MD=(b-a)
“ ” 则 例1. 设 M 为 M A B 解: D C ABCD 对角线的交点, b a AC = −2MA BD = −2MB 已知 b= a , b=0 a , b 同向 a , b 反向 a∥b 试用a 与b 表示 MA,MB,MC,MD. a + b = b − a = ( ) 2 1 MA = − a + b ( ) 2 1 MB = − b − a ( ) 2 1 MC = a + b ( ) 2 1 MD = b − a 机动 目录 上页 下页 返回 结束